РАЗДЕЛ 1. ЭЛЕКТРОДИНАМИКА.
Задача №1
За время t = 8 с при равномерно возраставшей силе тока в проводнике сопротивлением R = 8 Ом выделилось количество теплоты Q = 500 Дж. Определить заряд q, проходящий в проводнике, если сила тока в начальный момент времени равна нулю.
Решение.
Закон изменения тока: I = I(t) = kt,
где k – коэффициент пропорциональности.
Количество теплоты, выделившееся за время dt определим на основании закона Джоуля - Ленца, взятого в дифференциальной форме:
dQ = I2(t)R(t)dt.
Количество теплоты, выделившейся за все время:
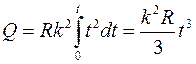 (1)
(1)
По определению сила тока:  , dq = I dt.
, dq = I dt.
Заряд, прошедший по проводнику за время t:
 (2)
(2)
Из (1): 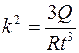 ;
;  .
.
Из (2):
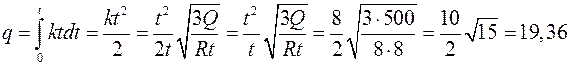 Кл.
Кл.
Ответ: q = 19,36 Кл.
Задача №2
Тороидальная катушка содержит N = 400 витков. Чему равна энергия магнитного поля, если при силе тока I = 2 А. Магнитный поток через сечение катушки Ф0 = 10-3 Вб.
Решение.
Запасенная энергия магнитного поля равна произведению плотности энергии wm на объем тороида V. wm = BH/2; Объем V = 2πR π(R - r)2, где R – радиус средней силовой линии тороида, r – внутренний радиус тора (радиус самой короткой силовой линии). Магнитный поток в торе Ф = В S = В π(R - r)2. Энергия W = wm V = (ВН/2)2πR (Ф/В). Подставив сюда напряженность магнитного поля внутри тороида Н = Ni/2πR, получим искомый результат:
W = nIФ/2 = 400×2×10-3/2 = 0,4 (Дж).
Задача №3
Соленоид, содержащий 103 витков, имеет длину 40 см и площадь поперечного сечения 10 см2.
Чему равен полный магнитный поток, пронизывающий соленоид, если ток в нем равен 1А.
Решение.
Магнитная индукция поля соленоида В = μ0nI, где n – число витков на единицу длины соленоида. Считая поле соленоида однородным, можно написать выражение для магнитного потока
Ф = nBS;
 (Вб).
(Вб).
Ответ: В = 10-3p = 3, 14.10-3 Вб.
Задача №4
Чему равен магнитный поток в стальном сердечнике (сталь Э1) в форме тороида, если сила тока в обмотке I = 0,5 А, число витков N = 1000, площадь сердечника 8 см2, R = 10 cм – радиус тороида.

r R
Решение
Задача решается аналогично предыдущим. Особенность состоит в том, что по найденной напряженности магнитного поля по таблицам необходимо найти магнитную проницаемость стали определенной марки.
Находим напряженность магнитного поля внутри тороида по формуле:
Н = NI/2πR = 103. 0,5/6.28. 0,1 = 0, 796. 103 А/м. По таблицам находим, что магнитная проницаемость μ = 200. Магнитная индукция В = μ μ0Н = 200. 4π.10-7. 0,796.103 = 0,2 Тл. Тогда магнитный поток в сердечнике Ф = В. S = 0,2.8.10-4 = 1,6. 10-4 Вб
Задача №5
Электроны в трубке движутся между пластинами заряженного конденсатора С, и их след на экране смещается на величину Х. Как надо направить магнитное поле  , что бы они попадали в точку O?
, что бы они попадали в точку O?
Решение.
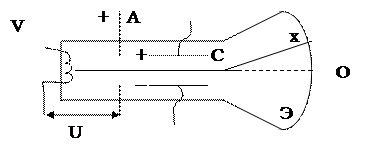 |
Рассмотрим движение электрона в магнитном поле. Если электрон движется в плоскости чертежа, а магнитное поле направлено перпендикулярно плоскости чертежа, то отрицательная заряженная частица отклоняется вниз, а положительная - вверх. Так как у нас движутся электроны, значит, чтобы след сместился на величину Х в точку О, нужно магнитное поле направить перпендикулярно в плоскость чертежа (рис.).

Два точечных заряда q1 = 3,3×10-9 Кл и q2 = -13,3×10-9 Кл находятся в точках с координатами (2,0,0) и (-2,0,0) соответственно. Найти:
1) величину и направление электрического поля в точке с координатами (0,3,4);
2) координаты точек, где поле отсутствует. Значения координат даны в сантиметрах.
Решение
Определим расстояния от точек, в которых расположены заряды, до точки наблюдения. Имеем r1= r2 =  см
см
Рассмотрим напряженность поля в заданной точке. Для этого определим единичные векторы  и
и  , задающие направление соответственно от первого и второго зарядов до указанной точки
, задающие направление соответственно от первого и второго зарядов до указанной точки
 = 1/(
= 1/( )
) 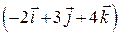
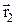 = 1/(
= 1/( )
) 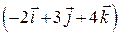 (в см)
(в см)
 |
Определим модули векторов напряженности поля в точке наблюдения, создаваемых первым и вторым зарядами. Учтем, что расстояние между зарядами и точкой наблюдения одинаковы и равны r =
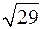 см, имеем:
см, имеем:
 = (k|q1| / (r2))
= (k|q1| / (r2))  ; Е2 = (k|q2| / (r2))
; Е2 = (k|q2| / (r2)) 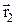 ,
,
Складываем векторы  и
и 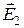 получаем вектор напряженности поля в точке наблюдения
получаем вектор напряженности поля в точке наблюдения
 =
=  +
+ 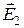 ; Ех = (к / r2 r)(-q1x1 –q2x2),
; Ех = (к / r2 r)(-q1x1 –q2x2),
Еy = (к / r3)*(-q1y1 –q2y2); Еz = (к / r3)(-q1z1 –q2z2)
= (9*109*103 / (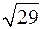 )3)((10-11)(3,3*4 – 13,3*4)).
)3)((10-11)(3,3*4 – 13,3*4)).
Определим точки, в которых напряженность поля равна нулю. Из анализа задачи ясно, что эта точка должна находиться на оси Х слева от заряда q1 на расстоянии х от него. Имеем:
F1 = kq1q / x2; F2 = kq2q / (4 + x)2;q1 / x2 = q2 / (4 + x)2;
(x + 4) / x =  ; x = 4 / (
; x = 4 / ( - 1).
- 1).
Задача №6
По четверти окружности радиусом R =5 см распределен заряд с линейной плотностью l = 6*10-6 Кл/м.
Найти напряженность Е и потенциал j поля в центре этой окружности.
Решение.
Выделим на окружности элемент длинной dl. Запишем для него выражение напряженности и потенциала:
dE = (tdl/4pee r2)×(r/r), где t - линейная плотность, r -расстояние: dj = tdl/4pee0r.
Запишем выражение напряженности в векторном виде:
Е = òdE и разложим на две составляющие dEy и dEx. Отсюда
E = òdE = `iòdEх + `jòdEу..
Определим dEх и dEу.
dEy = dE cosq, где q - угол между dE и dEy и q = 450, следовательно: dEy = dEcosq = tdlcosq/4pee0r -2.
Определим dl. Так как это дуга окружности, то ее длина будет определяться по формуле:
dl = Rdq, где R - радиус окружности, dq - элементарный угол, который она стягивает. Следовательно:
dEy = tRdq/4pee0r2cosq = t/4pee Rcosqdq.
Определим Ey, взяв интеграл с пределами от 0 до p/2
Следовательно: E = t/4pee R.
Теперь определим потенциал j поля: dj = tdl/4pee0 R,
так как
dl = rdj, то dj =  =
= 
Определим j, взяв интеграл
j = 
 =
=  =
=  =
= 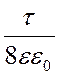 .
.
Задача №7
В бесконечном цилиндре радиуса R сделана коаксиальная полость радиуса R1. Вне цилиндра и в полости заряды отсутствуют, а в объеме распределены с плотностью r. Найти индукцию электростатического поля в полости, в цилиндре и вне его.
Решение
Для решения этой задачи воспользуемся теоремой Гауcса, взяв поверхность пронизывающуюся потоком вектора D в виде коаксиального цилиндра радиуса r.

 =Sgi,
=Sgi,
или заполнен через поток вектора  , т. е.
, т. е.
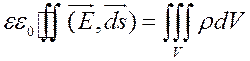 .
.
Определим D1, D2 и D3:
1) r < R1 т.е. в полости цилиндра.
В условии задачи сказано, что в полости цилиндра заряды отсутствуют, т.е. eqi = 0. Следовательно, r = 0. А это означает, что D1 = 0.
2) R1 < r < R, т.е. внутри цилиндра.
Здесь eqi ¹ 0, следовательно r ¹ 0.
Определим площадь внутренней части цилиндра: S = 2prl.
Определим объём: V = p l (r2 – R12).
Отсюда: D2 p r l = r p l(r2 – R12)
находим
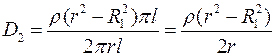 .
.
3) r > R, т.е. вне цилиндра
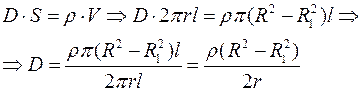
Задача №8
Магнитный поток Ф = 40 мВб пронизывает замкнутый контур. Определить среднее значение ЭДС индукции, возникающей в контуре, если за время t = 2 мс магнитный поток удвоился и возрастал равномерно.
Решение.
Среднее значение ЭДС индукции определим по формуле:
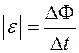 ,
,
где DF - величина изменения магнитного потока за время Dt.
Т.к. за время t = 2 мкс магнитный поток удвоился, то DF = Фк – Фн,
где Фк = 2Фн, Фк - конечноезначение, а Фн – начальное значение магнитного потока. Отсюда

Задача №9
Напряженность некоторого электростатического поля определяется выражением 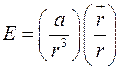 , где а – константа. Найти потенциал этого поля j(r).
, где а – константа. Найти потенциал этого поля j(r).
Решение.
Так как поле центрально симметричное, запишем связь между напряженностью поля и потенциалом в виде 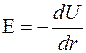 ;
;
отсюда dj = -Edr.
Определим потенциал, взяв интеграл от Е по dr, т.е.
 а
а 
отсюда
 .
.
Потенциал определяется с точностью до постоянной интегрирования.
Задача №10
Ток силой I = 2A циркулирует в контуре АВСД, имеющем форму равнобочной трапеции. Отношение длин оснований трапеции к = 2. Найти индукцию магнитного поля в точке Е пересечения продолжений боковых сторон трапеции. Меньшее основание трапеции ВС = L = 100 мм, высота трапеции BF = h = 50 мм.

Решение.
По условию дана равнобочная трапеция, продолжим её стороны до пересечения, получим точку Е, из неё проведём биссектрису ЕО = R = R1.
Получим угол ОЕД = a = 45°. Найдем напряжённость магнитного поля
Н = I/4pR(sina1 + sina2) = (I/4pR)2  /2 = I
/2 = I  /4pR;
/4pR;
где a1 и a2 равны a..
Зная, что высота трапеции равна h = R2, найдём напряжённость магнитного поля Н:

Ответ: напряжённость в точке Е составляет Н = 2,24 А/м
Задача №11

В одной плоскости с бесконечно длинным прямым проводом с током I = 5 A расположена прямоугольная рамка со сторонами а = 10 см и в = 20 см, как показано на рисунке. По рамке течет ток I1 = 0,2 A. Ближайшая сторона рамки находится на расстоянии d = 5см. Определить силу, действующую на рамку.
Решение.
Для решения данной задачи необходимо использовать выражение для напряжённости магнитного поля, создаваемого бесконечно длинным проводом.
Н =  . Тогда напряжённость магнитного поля создаваемого током I1 в верхнем плече рамки Нd =
. Тогда напряжённость магнитного поля создаваемого током I1 в верхнем плече рамки Нd =  , и нижнем плече рамки Нg =
, и нижнем плече рамки Нg = 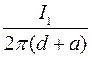 .
.
По условию задачи необходимо найти силу, действующую на рамку. Она будет состоять из двух компонент направленных в различные стороны и лежащих в плоскости чертежа: т.е. из сил Fб и Fg, действующих на проводники длины b, и сил F, действующих на боковые проводники длины а. Последние силы F различны по величине в разных участках проводника а, но на противоположных сторонах рамки они в соответственных точках равны по величине и противоположны по направлению, а поэтому в сумме дают нуль. Суммарная сила F = Fd - Fg. Силы действующие на боковые плечи рамки роли не играют. Найдём силу действующую на верхнее плечо рамки
Fd = I2bHdmo, и на нижнее Fg = I2bHgmo.
При сложении сил применяем «правило буравчика»:
F = Fd - Fg = (moI1I2b/2p)(1/d – 1/(d+a)) = 5,33 10-7 H
Ответ: F = 5,33×10-7H.
Задача №12
В однородное электрическое поле в вакууме перпендикулярно его силовым линиям со скоростью n влетает электрон. Длина области поперечного сечения поля равна L. На сколько процентов нужно изменить напряженность поля, чтобы отклонение электрона- при пролете поля изменилось на n процентов? Необходимо ли учитывать силу тяжести?
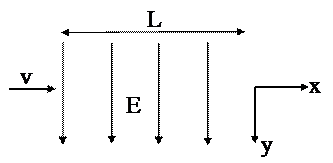
Движение по оси у равноускоренное
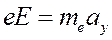 ;
; 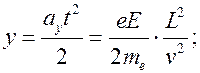
 - время пролета через поле при равномерном движении.
- время пролета через поле при равномерном движении.
Продифференцируем полученное выражение:
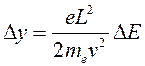 ;
; 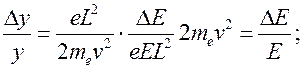
Следовательно, напряженность поля также следует изменить на n процентов.
Определим, при каких напряженностях Е сила тяжести, действующая на электрон, сравнится с силой, действующей со стороны электростатического поля:
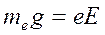 ,
,  .
.
Это поле чрезвычайно слабое. Поэтому при экспериментах с заряженными элементарными частицами пренебрегают влиянием силы тяжести в сравнении с влиянием электрических и магнитных полей.
Задача №13
Доказать, что напряженность поля, создаваемого бесконечной заряженной плоскостью в каждой точке пространства одинакова по величине и направлена перпендикулярно плоскости в данной точке.
Решение:
Рассмотрим заряд, распределенный по поверхности S с поверхностной плотностью s. Возьмем точку наблюдения А и поместим в нее заряд q на расстоянии R от плоскости S (OA ^ пл. S)
 |
Разобьем всю плоскость S на кольца шириной dr и в этих кольцах бесконечно близкими радиусами с углом dj между ними выделим элемент площади dS0, который можно рассматривать как несуществующий точечный заряд.
В точке наблюдения напряженность поля, создаваемого элементом кольца dS0, зависит от расстояния до этого элемента и от величины заряда на элементе кольца. Заряд dq элемента d S0 будет определяться выражением
dq = s×dS0. (1)
dS0 - элементарная площадь, которая, в свою очередь определяется выражением
dS0 = dr×dl, (2)
dl - дуга центрального угла dj, определяемая выражением dl = r×dj. Отсюда элементарная площадь определяется выражением
dS0 = r×dr×dj. (3)
напряженность электрического поля dE0 в точке А, созданная бесконечно малым (точечным) элементом заряженной плоскости dS0 определяется:
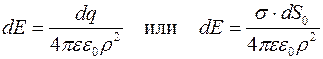 (4)
(4)
где r - расстояние от площади dS0 до точки наблюдения А.
Проинтегрировав это выражение по j мы тем самым найдем напряженность поля, создаваемого колечком шириной dr.
Но в точке А векторы dE, созданные различными площадками одного и того же колечка, образуют «веер», так как они направлены по образующим прямого кругового конуса с осью ОА и с вершиной в точке А.
Y - компоненты векторов dE при сложении взаимно компенсируются в силу цилиндрической симметрии задачи, а Х - компоненты суммируются алгебраически, что позволяет их проинтегрировать.
Подставляя в выражение (4) уравнение (3), имеем:
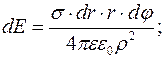 (5)
(5)
Проинтегрируем это выражение по dj, т.е.
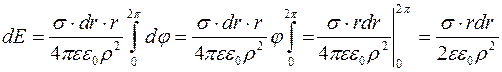 (6)
(6)
Напряженность поля Е определяется как:
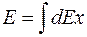 (7)
(7)
a dEx, как dEx = dEcosa (8)
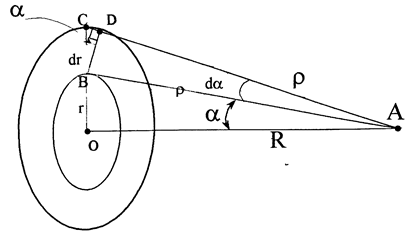 |
Как это видно из рисунка, BD = ds, ds - длина дуги BD радиуса r с центром в точке А, ÐCDB = 90°. Следовательно, напряженность поля по оси X, создаваемая колечком равна:
 (9)
(9)
В выражении (9) нам неизвестны расстояние r, радиус кольца r и угол a, под которым радиус r виден из точки А. Эти неизвестные величины необходимо связать. Введем угол da, под которым изменение радиуса dr видно из течки А. Из рисунка выразим такие величины, как: r, r, и dr.
Из DABD выразим BD, т.е.
BD = rda (10)
ÐCBD = da, поэтому
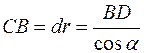 (11)
(11)
Рассмотрим DAOR и выразим из этого треугольника r и r:
r = Rtga, (12)
 (13)
(13)
Из DАВС выразим ОВ. т е
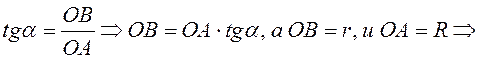
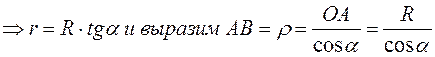
Подставляя выражения (10); (11);(12) и (13) в выражение (9), получим:

(14)
Теперь мы, подставляя выражение (14) в выражение (7) и интегрируя по a от 0 до p/2, получим напряженность поля, создаваемого бесконечной заряженной плоскостью.
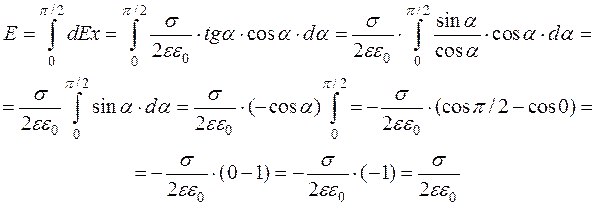 (15)
(15)
Выражение (15) показывает, что напряженность поля, создаваемая бесконечной заряженной плоскостью в каждой точке пространства одинакова по величине и направлена перпендикулярно плоскости в данной точке и не зависит от расстояния до этой плоскости.
Задача №14
Поток солнечной энергии за пределами атмосферы Земли составляет 2 кал/(см2.мин). Определить напряженности электрического и магнитного полей световой волны, считая, что этот поток переносится плоской волной.
Решение
Из уравнений Максвелла следует:
 ;
;
где Еm и Hm – амплитуды напряженностей полей.
Для прозрачных сред m = 1,  = n – показатель преломления.
= n – показатель преломления.
Плотность потока энергии, переносимого плоской волной (вектор Пойнтинга):
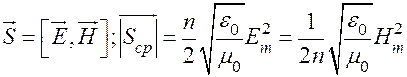 ;
;
Для вакуума (как и для воздуха) показатель преломления берем за единицу. Поэтому Еm = 1,03×103 В/м; Нm = 2,72 А/м.
Задача №15
Прямой провод, единица длины которого имеет сопротивление R, изогнут под углом 2a посередине. Перемычка из такого же провода перпендикулярна к биссектрисе этого угла и образует с согнутым проводом замкнутый треугольный контур. Этот контур помещен в однородное магнитное поле с индукцией В, перпендикулярное к его плоскости (см. рис). Перемычка движется вверх так, что тепловая мощность, выделяющаяся в цепи, постоянна и равна Р. Найти зависимость y(t) высоты подъема перемычки от времени, если y(0) = 0. Сопротивлением контактов пренебречь.
Решение
Пусть вектор В направлен вдоль оси oz (см. рис.). Так как при движении перемычки магнитный поток через плоскость контура по абсолютной величине возрастает, то индукционный ток направлен по часовой стрелке, и следует выбрать n = - `к. Тогда
ф = (В, n) S(y) = - BS(y),
где S(y) – площадь поверхности, ограниченной контуром, когда перемычка находится на высоте у. Следовательно, ЭДС индукции
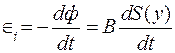
Силу индукционного тока находим по закону Ома
 (1)
(1)
Так как контур имеет форму равнобедренного треугольника, то его площадь S(y) = y2/tga. Сопротивление контура

Подставляя выражения для S(y) и R(y) в формулу (1), получаем

Тепловая мощность, выделяемая в цепи
 (2)
(2)
где
A = 2B2sin2a/ (Rcosa(1+sina)).
Из выражения (2) получаем дифференциальное уравнение для у
(y)1/2 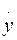 = (P/A)1/2 (3)
= (P/A)1/2 (3)
Так как Р = const, то, разделяя переменные и интегрируя уравнение (3), получаем
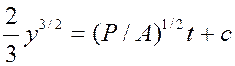
Поскольку у(0) = 0, то С = 0. Следовательно,

Задача №16
Сила тока в цепи нарастает по закону I = atn, где a - постоянный коэффициент. Количество теплоты, выделившейся в течение k- той секунды равно Q1. Определить заряд, прошедший через цепь за время t, если её сопротивление R.
Решение
Исходим из определения силы тока и интегрированием находим заряд. Затем используем закон Джоуля-Ленца
dq = Idt,  dQ = I2(t)Rdt;
dQ = I2(t)Rdt;

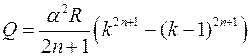 ; отсюда найдем
; отсюда найдем 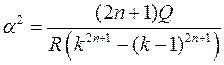 ;
;
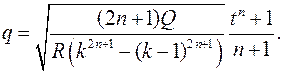 2n + 1 > 0; n > 0,5;
2n + 1 > 0; n > 0,5;
Задача
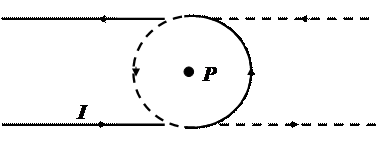
Длинный провод изогнут подобно шпильке для волос, как показано на рисунке. Получите точное выражение для магнитного поля в точке Р, находящейся в центре полуокружности.
 |
 Решение.
Решение.
Магнитное поле в точке Р, обусловлено током I в прямолинейных частях рассматриваемого привода, равно полю тока той же величины, протекающего в бесконечном прямолинейном проводе, расположенном от точки Р на расстоянии r. Поле, создаваемое током I вдоль полуокружности, равно в точности половине поля кругового тока I. Следовательно, в точке Р магнитное поле
B = 5 / 2 · μ0I / 2π r + 1 / 2 · μ0I / 2π r = μ0I / 4π r ·(2+π).
Оно определяется по правилу буравчика и направлено по нормали к плоскости чертежа.
Приведенное здесь решение станет очевидным, если ввести в рассмотрение другой идентичный контур, как показано на рисунке штриховой линией. Теперь мы имеем два бесконечных прямолинейных провода и один круговой контур – все с токами I. Поскольку поле в точке Р не зависит от поворота одного изогнутого провода относительно другого в плоскости чертежа и поля токов попросту суммируются, то поле тока в одном изогнутом проводе равно половине поля, обусловленного токами во всей рассматриваемой системе проводов.
 |
По прямому проводнику круглого сечения течет постоянный ток I. Найти поток электромагнитной энергии (вектор Пойнтинга) через боковую поверхность участка данного проводника, имеющего сопротивление R

Решение
По определению, вектор Умова – Пойнтинга, выражающий поток энергии, определяется по соотношению  , где
, где  - вектор напряжённости магнитного поля,
- вектор напряжённости магнитного поля, 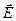 - вектор напряжённости электрического поля. Тогда по величине P = H E sin α, где α - угол между
- вектор напряжённости электрического поля. Тогда по величине P = H E sin α, где α - угол между 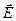 и
и  . В нашем случае
. В нашем случае 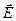
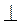
 , так как магнитное поле порождается электрическим током в проводе, причем направление совпадает с направлением напряжённости электрического поля в нём. Направление магнитного поля определяем с помощью правила буравчика. Поэтому Н
, так как магнитное поле порождается электрическим током в проводе, причем направление совпадает с направлением напряжённости электрического поля в нём. Направление магнитного поля определяем с помощью правила буравчика. Поэтому Н 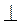 I и
I и 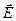
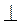
 , то есть α = 900, а sin 900 = 1).
, то есть α = 900, а sin 900 = 1).
Вектор Е направлен вдоль проводника, вектор Н направлен по касательной к поперечному сечению проводника. Поэтому вектор P направлен внутрь проводника перпендикулярно к его боковой поверхности, т.е. по радиусу к центру сечения проводника. Таким образом, энергия непрерывно поступает в проводник из окружающего пространства. Поток энергии через боковую поверхность проводника равен
Фs =P 2πr l, (*)
гдe P - модуль вектора Умова - Пойнтинга,
r - радиус сечения проводника,
l - его длина
Итак, P = H E (1)
Считаем ток в проводнике постоянным, а электрическое поле в нём однородным. Тогда Е = U/l,
где U - электрическое напряжение на концах проводника, l - его длина.
По закону Ома для участка цепи I = U/R, то U = I R,
где R - сопротивление проводника, Тогда
E = IR/l, (2)
По теореме о циркуляции вектора напряжённости магнитного поля
H = I/2πr, (3)
где I - сила тока в проводнике, r - радиус линии циркуляции вектора Н, равной длине концентрической с током окружности, длина которой равна периметру сечения проводника.
Подставляем (2) и (3) в (1), а затем в (*) получаем
Фs = P 2πr l = (I2 R/ 2πr l). 2πr l = I2 R.
Поток вектора Умова - Пойнтинга через боковую поверхность проводника равен мощности, рассеиваемой в проводнике электрическим полем, которая затем излучается в виде инфракрасного электромагнитного излучения поверхностью проводника и уходит в окружающее пространство.
Задача №17
Найти напряженность магнитного поля в точке А контура образованного отрезками прямолинейных проводников с токами. Совместить точку А (или В) с началом координат декартовой системы (ось х - горизонтальна; у – вертикальна; ось z направлена из листа). Найти силу, действующую на элемент тока 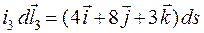 в этой точке (
в этой точке ( - бесконечно малая величина). Ток, создающий магнитное поле считать равным I = 13A, а стороны треугольника - а = 9, в = 10, с = 11. Считать точку А точкой пересечения биссектрис обтекаемого током треугольника.
- бесконечно малая величина). Ток, создающий магнитное поле считать равным I = 13A, а стороны треугольника - а = 9, в = 10, с = 11. Считать точку А точкой пересечения биссектрис обтекаемого током треугольника.

Решение
Приступим к вычислению напряженности магнитного поля в точке А. Она равна Н = На + Нв + Нс, т.к. по правилу буравчика векторы Н в этой точке направлены в одну сторону. По стандартной формуле
На =(i/4p r1) (sina1+ sina3), (1)
Нв =(i/4p r3) (sina1+ sina2) (2)
Нс =(i/4p r2) (sina3+ sina2) (3)
Обозначения ясны из рисунка.
Рассмотрим вначале геометрические соотношения в заданном треугольнике. Вычислим углы a1, a2, a3. Для этого, воспользовавшись теоремой косинусов, выразим из:
с2 = а2 +  2 - 2а
2 - 2а  × cos2a1
× cos2a1
cos2a1 = (а2 +  2 - с2)/2а
2 - с2)/2а  = 81 + 100 -121/2×9×10 = 0,333,
= 81 + 100 -121/2×9×10 = 0,333,
аналогично
cos2a2 = ( 2+с2-а2)/2
2+с2-а2)/2  с=81+121-81/2×10×11= 0,6363;
с=81+121-81/2×10×11= 0,6363;
cos2a3 = (а2+с2-  2)/2ас=81+121-100/2×9×11= 0,05151.
2)/2ас=81+121-100/2×9×11= 0,05151.
Выразим cosa1, cosa2, cosa3:

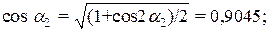

Вычислим углы a1, a2, a3 из значений косинусов
a1 = 35026439, a2 = 250241763, a3 = 290497929.
Из формулы sina = Ö1-cos2a вычислим sina1, sina2, sina3. Имеем:
sina1 = 0,4284, sina2 = 0,3154, sina1 = 0,4923.
Теперь из геометрии осталось найти r1, r2 и r3 - расстояния от точки А до соответствующих проводников с током.
Для нахождения r1 рассмотрим треугольник ВАС. Введем обозначения ВА = х, СА = у. Отсюда по теореме синусов:
х/ sina1 = а/ sing. <a = < ВАС.
х = а×sina1/sing.
Площадь треугольника ВАС S = а×х×sina3/2 в первом случае, где х×sina3 = r1 из треугольника ВАЕ.
Во втором случае:
S = а2×sina1 × sina3/2sin[p - (a1+a3)] =
= а2×sina1×sina3/2sin(a1+a3).
Теперь приравниваем эти площади и выражаем r1:
r1 = а×sina1×sina3/sin(a1+a3) =
= 9×0,4284×0,4923/0,9045×64,7623 = 2,0985.
Аналогично находим r2 и r3
r2 = с×sina2×sina3/sin(a2+a3) =
= 11×0,3154×0,4923/0,8165×54,7396 = 2,0918
r3 = в×sina1×sina2/sin(a1+a2) =
= 10×0,4284×0,3154/0,8704×60,5060 =1,5523
Подставляем найденные r1 =2,0985, r2 = 2,0918, r3 = 1,5523 в формулы (1), (2), (3). Получим: На = 0,4538, Нв = 0,4956, Нс = 0,39997. Находим суммарную напряженность в точке А:
Н = На + Нв + Нс = 1,3491 (А/м).
С учетом правила буравчика определяем вектор Н{0; 0; Нz }; Нz = -1,3491. Теперь находим силу, действующую на элементы тока в этой точке по формуле
d  1,2 = m04p
1,2 = m04p 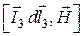
Из условия I3dl3 = {4; 8; 3}  .
.
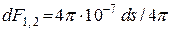
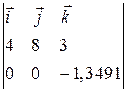
d  1,2 = (-(8×1,3491)
1,2 = (-(8×1,3491)  + (4×1,3491)
+ (4×1,3491)  )×10-7
)×10-7  =(- 0,7928
=(- 0,7928  +5,3964
+5,3964  )×10-7
)×10-7  [Н].
[Н].
РАЗДЕЛ 2. ГЕОМЕТРИЧЕСКАЯ И ВОЛНОВАЯ ОПТИКА.
Задача №1
Пучок рентгеновских лучей с длиной волны l = 244 нм падает на естественную грань монокристалла NaCl, плотность которого r = 2,16 г/см3. При зеркальном отражении от этой грани образуется максимум второго порядка. Определить угол скольжения a пучка лучей.
Решение.
Кристалл NaCl имеет кубическую решётку. Определим постоянную a этой решётки.
Молярная масса NaCl A = 22,99(Na) + 35,45(Cl) = 58,44 г.
В 58,44 г NaCl содержится число Авогадро молекул:
Na = 6,02×1023 (молекул), а в 2,16г (т.е. в 1см3) содержится искомое число n молекул. Составим пропорцию:
n = Nar/A = 6,02×1023×2,16/58,44 = 2,2×1022 (молек./см3)
тогда объём, приходящийся на одну молекулу,
V = 1/n = 1/2,2×1022 = 0,45×10-22 (см3)
Эту величину можно считать объёмом элементарной кристаллической ячейки. Следовательно, расстояние между атомами Na и Cl в этой ячейке будет:
ар = V1/3 = 3,6×10-10 (м).
По формуле Брэгга-Вульфа определим максимум второго порядка
2арsinaск = 2l; где aск – угол скольжения
sinaск = l/ap = 2,44×10-10/3,6×10-10 = 0,68;
Отсюда aск = 42, 67°.
Справочные таблицы дают для расстояния между атомами Na и Cl величину 5,63×10-10(м). В этом случае для угла скольжения aск1 получим
sinaск1 = 2,44×10-10/5,63×10-10 = 0,43.
Отсюда aск1 = 25,68°.
Ответ: a ск = 42,67°; aск1 = 25,68°.
Задача №2
Концентрация свободных электронов в ионосфере n0 = 4×107(см-3). Найти показатель преломления n для радиоволн с частотой n = 100 МГц.
Решение.
Для того чтобы определить показатель преломления необходимо определить плазменную (циклическую) частоту при заданной концентрации электронов
wр2 = noе2/meeo; где no – концентрация свободных электронов ионосферы; е – заряд электрона; me – масса электрона.
wр2 = 2,4×1013(1,6×10-19)2/9,1×10-31×8,85×10-12 = 7,63×1016
Отсюда wр = (7,63×1016)1/2 = 2,76×108 (с-1).
Определим циклическую частоту падающей радиоволны:
w = 2pn = 6,28×108(с-1).
Так как wр < w, то определим показатель преломления n следующим образом:
n2(w) = 1- wp2/w2 = 1 - 7,63/39,44 = 0,81, отсюда n = 0,9.
Ответ: n = 0,9.
Задача №3
Определить первый потенциал возбуждения атома водорода.
Решение.
Первый потенциал возбуждения соответствует переходу электрона с (n = 1) основного уровня на второй возбуждённый уровень (n = 2). По Бору энергия атома
W = -Rh/n2; где R – постоянная Ридберга, h – постоянная Планка, n – номер уровня.
Определим энергию перехода электрона с первого основного уровня на второй возбуждённый уровень
DW = Rh(1/n12 - 1/n22) = Rh/3 = 3,29×1015 ×6,63×10-34/3=
= 7,27×10-19 Дж.
С другой стороны известно, что DW = еDU, где е – заряд электрона, DU – разность потенциалов, пройденная электроном. В нашем случае – это потенциал возбуждения
DU = DW/e = 7,27×10-19/1,6×10-19 = 4,54 B.
Ответ: DU = 4,54 B.
Задача №4
Зеркало с коэффициентом отражения r, напыленное на тонкую пленку, вывели в космос на высоту h (малую в сравнении с радиусом Земли) с целью освещения приполярных областей. Считая известным поток солнечной энергии падающий на зеркало (солнечная постоянная – 1,4 кВт/ м2), найти освещенность, создаваемую им на Земле. Определить, при какой погонной массе зеркала (кг/м2) силы светового давления, действующие на него, сравняются с силами гравитационного воздействия.
Решение
Сила гравитационного воздействия на высоте h от Земли равна

m3 – масса зеркала, Мз – масса Земли, а на поверхности Земли
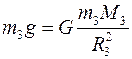 .
.
Отсюда:
 .
.
Сила давления света при нормальном падении лучей на зеркало

где: S – солнечная постоянная (1,4. 103 Вт/м2); С0 – скорость света; А – площадь зеркала.
Сравним F гр и F св. Получим:

Рассмотрим связь между освещенностью и яркостью зеркальной поверхности, создающей эту освещенность.
Освещенность, создаваемая поверхностью с яркостью В площадью S, находящейся на расстоянии h от земли составляет
Е = Bdw,
где dw - телесный угол, под которым видно зеркало с поверхности Земли: dw = S/h2.
Яркость зеркала диффузно переотражающего солнечные лучи находим по формуле B = rEc/p,
где Ес – освещенность, создаваемая солнцем на зеркале, Ес = 1,4.105 лк.
Задача №5
На плоскопараллельную стеклянную пластинку падает под углом Брюстера узкий пучок естественного света. Коэффициент отражения R = 0,080. Определить степень поляризации света, прошедшего через пластинку.
Решение.
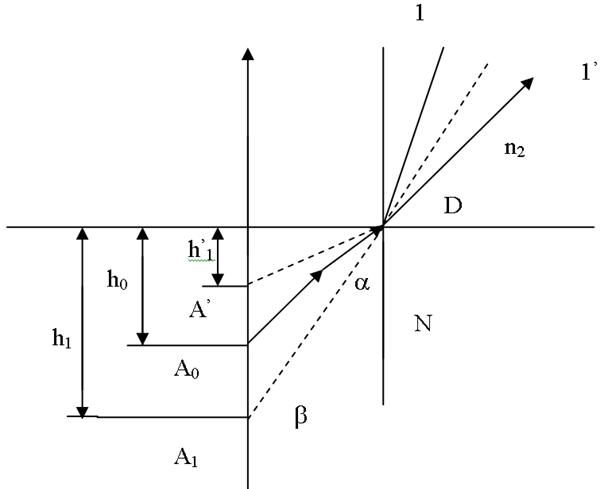
Проведем анализ условия задачи. Для описания изменения поляризации света при отражении и преломления на границе раздела сред, пользуются понятием степени поляризации
P = (I1-I2)/(I1+I2), (1)
где I1 и I2 – интенсивности плоско поляризованных компонентов пучка, у которых вектор Е перпендикулярен или параллелен плоскости падения (т.е. плоскости, в которой лежит падающий луч и нормаль, восстановленная к границе раздела в данной точке падения).
Очевидно, что сумма, стоящая в знаменателе выражения (1), равна полной интенсивности пучка. Чтобы найти степень поляризации в пучке 4 (рис.), разберем детально, как происходит поляризация света при прохождении его через стеклянную пластинку.
Падающий свет, по условию, естественный, поэтому
I0^= I0ll = 0,5 I0. (2)
Степень поляризации естественного пучка, следовательно, равна нулю. При падении света на изотропный диэлектрик под углом Брюстера отражаться может только та компонента, в которой вектор 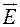 колеблется перпендикулярна плоскости падения. Поэтому луч 1 будет полностью поляризован (степень поляризации равна 1). Световой пучок, прошедший через верхнюю поверхность пластинки (луч 2), содержит компоненту, в которой вектор
колеблется перпендикулярна плоскости падения. Поэтому луч 1 будет полностью поляризован (степень поляризации равна 1). Световой пучок, прошедший через верхнюю поверхность пластинки (луч 2), содержит компоненту, в которой вектор 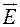 колеблется в плоскости падения (на рисунке обозначена ll), и компоненту, в которой вектор
колеблется в плоскости падения (на рисунке обозначена ll), и компоненту, в которой вектор 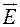 колеблется нормально плоскости падения (на рисунке обозначена *). Пучок 2 будет частично поляризован, т.к. обе компоненты присутствуют не в равной мере. Так как луч 2 падает на нижнюю поверхность пластины тоже под углом Брюстера, то луч 3, отраженный от нее, так же полностью поляризован с колебаниями вектора
колеблется нормально плоскости падения (на рисунке обозначена *). Пучок 2 будет частично поляризован, т.к. обе компоненты присутствуют не в равной мере. Так как луч 2 падает на нижнюю поверхность пластины тоже под углом Брюстера, то луч 3, отраженный от нее, так же полностью поляризован с колебаниями вектора 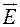 перпендикулярными плоскости падения. Свет, прошедший через обе поверхности, (луч 4), поляризован частично. Для определения степени поляризации этого пучка необходимо рассчитать интенсивность обеих компонент пучка. Поскольку пучки 1 и 3 содержат только импульсы, в которых вектор
перпендикулярными плоскости падения. Свет, прошедший через обе поверхности, (луч 4), поляризован частично. Для определения степени поляризации этого пучка необходимо рассчитать интенсивность обеих компонент пучка. Поскольку пучки 1 и 3 содержат только импульсы, в которых вектор 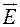 колеблется перпендикулярно плоскости падения, то, очевидно, что
колеблется перпендикулярно плоскости падения, то, очевидно, что
I4ll > I0^ и I4 ll = I0ll (3)
(Здесь и в дальнейшем нижний цифровой индекс соответствует номеру своего пучка). Значение I4^ зависит от коэффициента отражения, равного отношению интенсивности отражения света к интенсивности падающего: R = I1/I0
Так угол падения равен углу Брюстера, то I1 = I1^ и соответственно равен (см.(2)):
R = I1^/I0 = I1^/2 I0^ I (4)
Согласно теории Френеля, отношении интенсивности отраженного света к интенсивности падающего для выбранного направлений колебания вектора 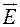 (в данном случае для E^) зависит только от суммы (либо от разности) углов падения и преломления. Поскольку данная пластинка плоскопараллельная, условия отражения на верхней и нижней гранях одинаковы, поэтому с учетом выражения (4) можно записать:
(в данном случае для E^) зависит только от суммы (либо от разности) углов падения и преломления. Поскольку данная пластинка плоскопараллельная, условия отражения на верхней и нижней гранях одинаковы, поэтому с учетом выражения (4) можно записать:
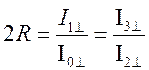 (5)
(5)
Дадим расчет. В световом пучке, прошедшим через верхнюю поверхность пластинки, I 2^= I 0^ – I1^ и, согласно (5),
I 2^= I 0^(1-2R) (6)
Очевидно, что интенсивность соответствующих компонентов в световом пучке, прошедшем через нижнюю поверхность,
I4^ =I 2^ - I3^ (7)
Подставим выражение (6) и (5) в (7):
I4^ =I 0^(1-2R)2 =0,5 I 0(1-2R)2
Подставим выражение (8), (3), (2) в (1), найдем окончательно
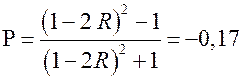



Задача №6
Светящаяся точка, находящаяся в среде с показателем преломления n1, рассматривается невооруженным глазом из среды с показателем преломления n2. Каково будет кажущееся расстояние точки до границы раздела сред, если точка находится от этой границы на расстоянии h0, а глаз расположен так, что в него попадают лучи, падающие на границу раздела под небольшими углами?
Решение
Допустим, что светящаяся точка A0 (рис.) находится в среде с показателем преломления n1 и глаз наблюдателя расположен над предметом в среде с показателем преломления n2 так, что в него попадают лучи, идущие под малыми углами к нормали N. Выберем из пучка лучей, попадающих в глаз наблюдателя, два луча A0C и A0D. Первый луч падает перпендикулярно границе раздела сред и идет во вторую среду не преломляясь. Второй луч, переходя во вторую среду, отклоняется от своего начального направления. Рассмотрим два случая: когда n1 > n2 (глаз расположен в оптически менее плотной среде) и когда n1 < n2 (глаз помещен в среде оптически более плотной, чем среда, где находится источник).
Если луч A0D переходит в среду менее плотную, он откланяется от своего начального направления, удаляясь от нормали в точке D, и идет по направлению 1/. Если же луч переходит в среду более плотную, он приближается к нормали и идет по направлению 1. В первом случае лучи, вышедшие из точки A0, кажутся наблюдателю выходящим из A/1, во втором – из A1. Эти точки являются мнимым изображением предмета A0, расстояние которых h/1 и h1 от границы раздела сред определяются следующим образом.
Допустим, что угол падения луча в точке D равен a,
угол преломления оказывается равным соответственно b и b1
Тогда, как видно из чертежа, в треугольниках A0DC и A1DC сторона СD является общей.
Поэтому можно записать
CD = h0 tga = h1 tgb ( или h0 tg a = h1 tg b1)
откуда
h1= h0 * 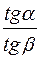 (h1= h0*
(h1= h0* 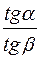 ).
).
Поскольку лучи падают на границу раздела сред под небольшими углами, то вследствие малости a и b тангенсы этих углов можно заменить их синусами
h1 = h0* 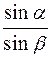 (h11=h0*
(h11=h0* 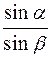 ).
).
по закону преломления 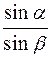 =
=  , следовательно, h1=h0*
, следовательно, h1=h0*  .
.
Такой же результат получается и для второго случая. Как показывают приведенные расчеты и построения, светящийся предмет А будет казаться наблюдателю ближе к поверхности раздела h1 < h0 , если вторая среда менее плотная n1 < n2 (например, из воздуха рассматривается предмет, находящийся в воде). Если же смотреть на светящуюся точку из среды оптически более плотной (например, из воды в воздух), то точка будет казаться дальше, чем она находится на самом деле, поскольку при n2 > n1 имеем h1 > h0
Задача №7
Узкий пучок естественного света проходит через газ из оптически изотропных частиц. Найти степень поляризации света, рассеянного под углом θ к лучу
в рассеянном пучке амплитуда светового вектора перпендикулярного плоскости падения не изменяется а амплитуда вектора в плоскости падения связана с Е0 граничным условием (см. объяснение явления Брюстера)
Е|| = Е0 sin (900 - θ) = Е0 cos θ
Таким образом, в рассеянном пучке максимальная интенсивность светового поля
Imax = Е0 2, а минимальная - Imшт = Е0 2 cos2 θ
по определению степени поляризации
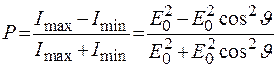 =
= 
Найти разность углов: критического при полном внутреннем отражении и угла Брюстера (угла полной поляризации) при отражении световой волны на границе раздела двух прозрачных сред с показателями преломления n1 и n2. Построить ход лучей при отражении. Принять n1 = 1,5 n2 = 1,9.
Решение.
При переходе луча из оптически более плотной среды в менее плотную при угле падения большем (или равном) критического имеет место полное внутреннее отражение, когда вся энергия падающего луча уходит в отраженный луч, а преломленный луч (боковая волна) скользит вдоль границы раздела сред (см. рис.).

Из закона преломления имеем
n2 sin xкр = n1 sin 90o sin xкр = n1/n2 = 1.5/1.9 = 0.7895.
α кр = 52о,1363
Рассмотрим явление Брюстера. Оно состоит в полной поляризации отраженного от плоской границы раздела двух диэлектриков (или прозрачных сред в оптике) луча (неполяризованной электромагнитной волны). Из формул Френеля следует, что в отраженном свете может отсутствовать волна, электрический вектор которой лежит в плоскости падения.
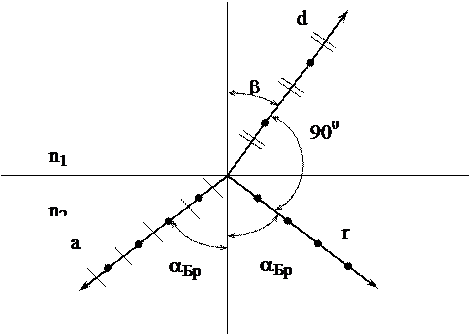
Пусть а – неполяризованная падающая волна. Если она падает под таким углом αБр,
что tg αБр = n1/n2,, (1)
то в отраженной волне r остается только та поляризация, для которой электрический вектор Е перпендикулярен плоскости падения (плоскости чертежа).
В преломленной волне преобладает поляризация, параллельная плоскости падения и эта волна, таким образом, частично поляризована.
Из § 112 “Курса общей физики” И.В. Савельева и “Справочника по физике ” Б.М.Яворский, А.А.Детлаф (с. 588) после преобразований берем коэффициент отражения в виде:
Rp = (n1cosα2 - n2cosα1) /(n1cosα2 + n2cosα1) (1)
- коэффициент отражения для поляризации параллельной плоскости падения. Rp = 0, если
n1cosα2 = n2cosα1 (2)
Закон преломления n2sinα2 = n1sinα1 (3)
Возведем (2) в квадрат и получим n 12 cos 2 α2 = n 22 cosα 12,
или n 12(1 – sin2α2) = n 22(1 – sin2α1). (4)
Из (2) sinα1 = n2 sinα2 / n1.
Покажем, что угол между отраженной






