Далее, если считать, что приведенная выше последовательность изображает число в системе счисления с основанием r, то каждая из цифр этой последовательности может принимать одно из значений диапазона
r-1 >=аi>=0 (1.2)
0 ÷ 9 – в десятичной, 0 ÷ 1 – в двоичной.
Для оценки количественного значения каждого разряда числа используется основание системы счисления, которое указывает, во сколько раз единица i+1 разряда больше единицы i предыдущего младшего разряда Таким образом, заданное число можно представить так
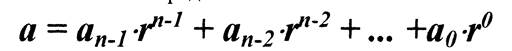 (1.3)
(1.3)
Данное выражение используется для записи чисел в любой позиционной системе счисления. Рассмотрим в качестве примера широко известную десятичную систему счисления, в которой для обозначения используется десять цифр (0,1,2,3,4,5,6,7,8,9) и за основание взято число десять (10).
Запишем пару чисел 230 и 127 десятичной системы счисления, пользуясь указанным выше выражением
1) 230 = 2•102 + 3•101 + 0•100
2) 127 = 1•102 + 2•101 +7•100
Двоичная система счисления
Основанием двоичной системы счисления является число два. Любые числа в этой системе изображаются последовательностью цифр 0 и 1. При этом каждый старший разряд больше соседнего младшего в два раза.
Для получения значения двоичного числа 10101 в десятичной системе счисления достаточно вычислить написанное выражение
101012 = 1 •24 + 0 •23 + 1 •22 + 0 •21 + 1 •2° = 16 + 0 + 4 + 0 + 1 = 2110
В дальнейшем основание системы счисления будем указывать в качестве нижнего индекса у самой правой цифры числа, например 12510 - десятичная система счисления, 10112 - двоичная система счисления.
В двоичной системе счисления целые десятичные числа от нуля до девяти соответственно изображаются так
Табл. 1.5
| Десятичная | ||||||||||
| Двоичная |
Шестнадцатеричная система счисления
Вскоре появилась необходимость в адресации 2 байт, которые назвали "словом". Для такой адресации было явное преимущество использования шестнадцатеричной системы исчисления перед восьмеричной, т е системы для адресации 8 • 2=16 бит
В шестнадцатеричной системе счисления используется следующие цифры и символы 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, А - десять, В - одиннадцать, С - двенадцать, D - тринадцать, Е - четырнадцать, F - пятнадцать. За основание системы счисления берется число шестнадцать, изображаемое как 10.
Например, для числа
5A316=5·16²+10·161+3·160 = 5·256 +10·16+3·1= 1280+160+ 3= 144310
Таблица перевода чисел из шестнадцатеричной системы в другие
| 016 | = | 010 | = | 08 | = | ||||
| 116 | = | 110 | = | 18 | = | ||||
| 216 | = | 210 | = | 28 | = | ||||
| 316 | = | 310 | = | 38 | = | ||||
| 416 | = | 410 | = | 48 | = | ||||
| 516 | = | 510 | = | 58 | = | ||||
| 616 | = | 610 | = | 68 | = | ||||
| 716 | = | 710 | = | 78 | = | ||||
| 816 | = | 810 | = | 108 | = | ||||
| 916 | = | 910 | = | 118 | = | ||||
| A16 | = | 1010 | = | 128 | = | ||||
| B16 | = | 1110 | = | 138 | = | ||||
| C16 | = | 1210 | = | 148 | = | ||||
| D16 | = | 1310 | = | 158 | = | ||||
| E16 | = | 1410 | = | 168 | = | ||||
| F16 | = | 1510 | = | 178 | = |
Лекция 3
Двоичная арифметика
Арифметические операции в двоичной системе счисления выполняются по правилам, указанным в таблице 1.6.
Табл. 1.6
Над числами в двоичной системе счисления можно выполнять арифметические действия.
При этом используются следующие таблицы:
| Сложение | Вычитание | Умножение |
| 0+0=0 | 0-0=0 | 0*0=0 |
| 1+0=1 | 1-0=1 | 1*0=0 |
| 0+1=1 | 1-1=0 | 0*1=0 |
| 1+1=10 | 10-1=1 | 1*1=1 |
Рассмотрим примеры:
| Запись операции | Расчет столбиком |
| 1 1 0 1 0 12 + 1 1 0 1 12 | 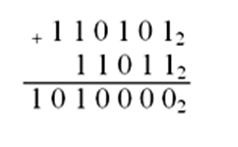
|
| 1 1 0 1 12 - 1 1 0 12 | 
|
| 1 1 0 1 12 * 1 0 12 | 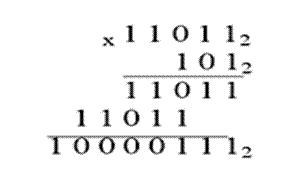
|
Для деления в двоичной системе счисления нужно уметь сравнивать числа (определять, какое больше) и хорошо вычитать. Посмотри деление на анимированном примере Пример:

| 
|
| Еще несколько примеров: | 
|
Пример сложения «столбиком» (14 + 5 = 19):
| + | |||||
Пример умножения «столбиком» (14 × 5 = 70):
| × | |||||||
| + | |||||||
Двоичная система счисления широко используется для представления данных в вычислительных машинах. Это связано с тем, что в этой системе счисления очень просто выполняются арифметические и логические действия, а для представления двоичных чисел в машине можно использовать достаточно простые электронные элементы.






