Полная математическая модель плоского изгиба и
Растяжения (сжатие) прямого стержня
Постановка задачи. Параметры
Выше мы построили математическую модель и проанализировали частный случай нагружения прямого стержня – растяжение – сжатие. Рассмотрим более общую постановку задачи определения внутренних сил и перемещений в прямом стержне при его плоском изгибе и растяжении-сжатии. Задача решается в главных центральных осях. При этом, в отличии от предыдущей задачи, внутренние силы Mx и Qy не равны нулю. Соответственно, дополнительно имеют место перемещения v оси вдоль оси y, а также касательные напряжения в поперечном сечении. Вычисление последних через внутренние силы - сложная задача и будет рассмотрена приближенно в следующей лекции. Пока ограничимся построением математической модели связи внутренних сил и перемещений. Основные параметры вычисляются в исходных главных центральных осях.
Итак, параметры задачи – шесть неизвестных функции от координаты сечения:
- продольная сила N(z),
- поперечная сила Q(z),
- изгибающий момент Mx(z),
- продольное перемещение w(z),
- поперечное перемещение v(z),
- угол поворота сечения относительно оси x 
,
появление которых является следствием действующих внешних нагрузок на определенным образом закрепленный стержень. В схеме приложения нагрузок две погонные нагрузки qy и qz. В частных случаях они вырождаются в сосредоточенные продольную силу Pz, поперечную Py и момент L.
Геометрические соотношения
На рис. 5.1 изображено положение отрезка dz стержня с координатой z, отмеренной от левого конца стержня до нагружения, и положение того же отрезка длиной dz1 после нагружения распределенной по длине нагрузкой qy, qz.
Введены обозначения: v, w – перемещения оси стержня по оси y и z соответственно; φ – угол поворота сечения относительно оси х.
Проектируя замкнутый контур АА1В1ВА на оси Y и Z, получаем два геометрических соотношения:
(5.1)
(5.2)
 |
Уравнения равновесия
Проектируя силы, действующие на отрезок dz1, на оси координат (рис. 5.1) и рассматривая момент сил относительно точки В1, пренебрегая бесконечно малыми второго порядка малости, получаем три уравнения равновесия в неподвижной системе координат:
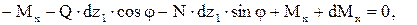
Физические зависимости
При схематизации деформаций в главных центральных осях получено
. 
Пренебрегаем изменением ГХС при малом повороте осей нормальная сила в повернутом сечении
.
С другой стороны, Qz, Qy есть сумма проекций N и Q на оси Z1 , Y1 (рис. 5.1):
,
.
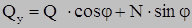Приравниваем полученные выражения и после преобразований с учетом (5.2)
.
Но из (5.2) dz1 = (dz + dw)/cosφ, следовательно,
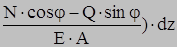. (5.3)
Учитывая, что 
, запишем формулу для распределения нормальных напряжений в сечении стержня в виде
.
Математическая модель плоского изгиба и растяжения прямого стержня при больших перемещениях
Подставляя выражение (5.3) в (5.1), (5.2), после элементарных преобразований получаем систему дифференциальных уравнений для определения параметров v, w, j, N, Q, Mx:
,
,
,
,
Система шестого порядка, не линейна, содержит трансцендентные выражения и не имеет решений в элементарных функциях.
Шесть граничных условий для конкретной задачи всегда формулируются, так как при любом закреплении концов стержня, на каждом известны по три условия:
- жесткое закрепление v = 0, w = 0, j = 0;
- шарнирно-неподвижное закрепление Mx = 0, v = 0, w = 0;
- шарнирно-подвижное закрепление Mx = 0, v = 0, N = 0;
- свободный конец Mx = 0, Qy = 0, N = 0 и т.д.
Система дифференциальных уравнений записана в каноническом виде, не требующем предварительного преобразования для численного интегрирования.
