План заняття:
1. Загальні відомості про похибки вимірювань.
2. Класифікація помилок вимірювання.
3. Властивості випадкових помилок.
4. Поняття про середнє арифметичне значення.
5. Середня квадратична похибка одного вимірювання.
Велика різноманітність геодезичних робіт, пов'язаних з дослідженням, проектуванням, будівництвом і експлуатацією будівель та споруд, передбачає вимірювання кутів, відстаней, площ або перевищень з використанням приладів, інструменту та пристроїв. На точність вимірювань впливають технічні характеристики приладів, кваліфікація і уважність спеціалістів, умови праці та багато інших факторів.
Вимірювання — це процес порівняння деякої одиниці міри з вимірюваною величиною. Результатом вимірювання є число, яке показує скільки разів одиниця міри вміщується у вимірюваній величині. Всі одержані результати поділяються на прямі або безпосередні і непрямі, або посередні.
Прямим називається результат, який одержано при безпосередньому вимірюванні якоїсь величини з використанням відповідних приладів, інструменту чи пристроїв.
Посереднім, або непрямим, результатом називають величину, одержану як функцію інших безпосередньо визначених величин.
Щоб одержати значення певної величини взагалі, достатньо виконати вимірювання один раз. Таке вимірювання називається необхідним. При цьому немає ніякої впевненості в тому, що одержане значення дійсно відповідає цій величині.
Надлишкові вимірювання виконують для контролю правильності отриманих результатів вимірювання
Практично доведено, що одне вимірювання, як би якісно воно не виконувалось, не може бути абсолютно точним. Результати вимірювань завжди мають похибки, а тому обов’язково треба виконувати не менше двох вимірювань, а при деяких геодезичних роботах — значно більше.
Відхилення результату вимірювання величини від її точного значення називають похибкою, (помилкою) вимірювання.
∆=l-Х
∆ - похибка вимірювання - відхилення результату вимірювання від дійсного значення вимірюваної величини;
l — результат вимірювання;
X — дійсне значення величини.
Результати вимірювань завжди супроводжуються помилками. Помилки вимірювань класифікуються по двом ознакам: по характеру дії, по джерелу походження. Помилки по характеру дії бувають: грубі, систематичні, випадкові.
Груба помилка – промах виконавця (по своїй абсолютній величині значно перевищують допустимі межі). Виникають через неуважність під час вимірювання, призводить до прорахунків, описок, вимірювання не тих предметів. Для виключення грубих помилок предмет вимірюють два і більше разів.
Систематичними помилками називають такі помилки, які при повторних вимірюваннях залишаються без змін, змінюються по певному закону, або змінюючись випадково зберігають знак. Систематична помилка може бути виключена із одиничного виміру.
Випадкові помилки – іноді їх називають неминучими, виникають в результаті впливу великого числа факторів, їх закономірність виявляється тільки у масовому проявленні.
По джерелу походження помилки бувають: особисті, приладів, зовнішні.
Особисті – залежать від органів чуття спостерігача
Помилки приладів – зумовлені недосконалістю геодезичних приладів або неточною юстировкою.
Зовнішні помилки – зумовлені впливом природних умов (температура повітря, видимість, вітер).
Причинами виникнення випадкових помилок може бути:
▬ недосконалість приладів (грубі штрихи, недостатнє збільшення);
▬ недосконалість органів чуття;
▬ нерівномірний вплив середовища;
▬ прийнята методика вимірювання;
▬ кваліфікація виконавця.
Ряд випадкових похибок рівно точних вимірювань має такі властивості:
1. Помилки по абсолютній величині не перевищують деякої граничної величини, тобто  ;
;
2. Малі за абсолютним значенням похибки зустрічаються значно частіше, ніж великі;
3. додатні і від’ємні похибки рівні по абсолютній величині зустрічаються в ряду приблизно однаково часто;
4. Середнє арифметичне значення з випадкових похибок рівно точних вимірювань при необмеженій кількості вимірювань прямує до нуля 
Просте середнє арифметичне при необмеженій кількості рівно точних вимірювань прямує до дійсного значення.
Якщо отриманий ряд результатів рівно точних вимірювань однієї і тієї ж величини, то проводять їх математичну обробку, при якій обчислюють:
1. середнє арифметичне значення виміряної величини (як найбільш надійне);
2. середню квадратичну похибку одного вимірювання;
3. середню квадратичну похибку середнього арифметичного.
Середнє арифметичне значення ї з результату рівноточних вимірювань l1, l2,,….ln, які також називаються арифметичним середнім, визначається по формулі 
Для спрощення обчислення середнього арифметичного зазвичай вводять наближене значення вимірюваної величини l0. Вибравши приблизне значення, обчислюють залишки ε і = li-l0 (і=1,2,…n).
Приблизне значення вибирають з таким розрахунком, щоб залишки ε і були малі. Часто за l0 приймають найменше значення із li
Із попередньої рівності li = l0+ ε і (і=1,2,…n).
Підставивши цей вираз в формулу після деяких перетворень отримаємо 
Ця рівність служить для обчислення середнього арифметичного через приблизне значення.
Якщо величина виміряна n разів з рівно точним результатом l1,l2,….,ln то за справжнім значенням цієї величини обчислюють випадкові помилки ∆ кожного з результатів.
L0 – справжнє, або наймовірніше значення визначене як середнє арифметичне.
∆1= L0-l1
∆2= L0-l2
∆n= L0-ln
За ними оцінюють точність вимірювань обчислюючи середню квадратичну помилку одного вимірювання – m

Дійсна помилка може перевищувати граничну в п’ятьох результатах із 100.

Оцінка точності найймовірнішого значення 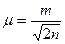
Отримавши значення m знаходять середню квадратичну помилку середнього арифметичного по формулі 
Контрольні запитання:
1. Що називають вимірюванням?
2. Охарактеризуйте прямі та непрямі вимірювання.
3. Які властивості мають випадкові помилки?






