Пусть заданная на действительной оси функция может быть продолжена на верхнюю полуплоскость 
комплексной плоскости так, что аналитическое продолжение 
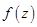является аналитической функцией в области всюду за исключением конечного числа изолированных особых точек, причем 
Тогда
Пусть 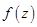может быть продолжена на верхнюю полуплоскость комплексной плоскости так, что 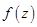не имеет особых точек на оси 
, является аналитической в верхней полуплоскости всюду за исключением конечного числа изолированных особых точек и равномерно относительно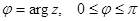 
стремится к нулю при 
Тогда для 
Отсюда
Пусть 
- рациональная функция 
, непрерывная внутри промежутка интегрирования.
Полагая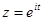 
, получим 
Тогда
,
где вычеты функции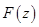 
вычисляются относительно всех особых точек, принадлежащих области 
.
Конформные отображения
Геометрически заданную на области 
функцию 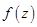можно рассматривать как отображение области плоскости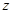 
на некоторое множество плоскости 
, являющееся совокупностью значений 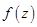, соответствующих всем 
. Взаимно однозначное отображение области плоскости на область плоскости 
называется конформным, если в каждой точке области оно обладает свойствами сохранения углов и постоянства растяжения. Для того, чтобы отображение области , задаваемое функцией 
, было конформным, необходимо и достаточно, чтобы была однолистной и аналитической в области функцией 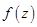, при этом 
всюду в области .
Например, отображение, осуществляемое линейной функцией 
можно представить в виде композиции гомотетии, поворота и параллельного переноса плоскости. При этом любая окружность отображается на окружность, любая прямая – на прямую, любой открытый круг – на открытый круг, любая открытая полуплоскость – на открытую плоскость. Отображение может быть получено по двум парам точек 
и 
.
Отображение, осуществляемое дробно-рациональной функцией 
можно представить в виде композиции параллельного переноса, инверсии, осевой симметрии, гомотетии и поворота плоскости. При этом любая окружность, не проходящая через точку 
, отображается на окружность; окружность, проходящая через точку - на прямую; любая прямая, не проходящая через точку - на окружность; прямая, проходящая через точку – на прямую; любой открытый круг, для которого точка - является внешней – на открытый круг; открытый круг, для которого точка - является граничной – на открытую полуплоскость (и обратно). Дробно-рациональное отображение может быть получено по трем парам точек , и 
.
Функция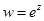 
однолистна в любой полосе шириной менее 
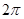, параллельной действительной оси. Она отображает полосу 
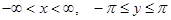на всю плоскость с разрезом по действительной отрицательной полуоси. Вся плоскость 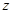отображается на бесконечнолистную риманову поверхность.
Обратная функция 
однозначна на этой римановой поверхности, а ее главное значение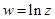 
определяет отображение всей плоскости 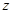с разрезом 
на полосу 
.
