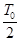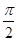Качество результата измерения определяется величиной содержащейся в нем погрешности. Поэтому при измерении необходимо стремиться к тому, чтобы получить результат с минимальной погрешностью. Основными факторами, вызывающими появление погрешности результата измерения являются: метод измерения, несовершенство средства измерения, влияние условий измерения на параметры средств измерений и на измеряемую физическую величину и ее характер. Поэтому для получения высокоточных результатов необходимо создавать средства измерения, которые обладали бы малой инерционностью (W 0(р) = 1) и минимальным отклонением коэффициента чувствительности от номинального значения (D k = 0), а также устойчивостью к внешним возмущающим воздействиям.
В реальных условиях при решении конкретных измерительных задач результат все равно будет содержать погрешность, поэтому для ее оценки и исключения из результата измерения необходимо использовать эффективные алгоритмы. Одним из путей решения этой проблемы – это применение многократных измерений и последующая обработка их результатов.
Многократное измерение – это измерение, при котором результат представляется совокупностью нескольких возможных значений. Результат измерения по своей природе всегда является случайной величиной. По определению каждая случайная величина связана с некоторым множеством возможных значений (конечным – для дискретной величины, несчетным – для непрерывной случайной величины). При измерении результат принимает одно из значений этого множества случайным образом. Повторяя измерения можно получить результаты многократных измерений.
Процесс многократных измерений достаточно длительный по времени, причем каждое возможное значение появляется в определенный фиксированный момент времени. Это означает, что совокупность возможных результатов измерений при многократных измерениях представляет упорядоченную совокупность – некоторую функцию дискретного аргумента времени, или иначе – последовательность. В практике измерений количество дискретных значений аргумента можно представить как у (tk), и k = 
где у (tk) – возможное значение результата измерения в момент tk. Такую последовательность принято называть «выборкой объема n».
Последовательность у (tk), k = содержит больше информации об измеряемой физической величине, чем однократное измерение, при котором результат принимает одно возможное значение, поэтому на ее основе можно получить более точную оценку значения измеряемой физической величины.
Таким образом, задача обработки результатов многократных измерений сводится к тому, чтобы построить такое преобразование случайной последовательности у (tk), k = которое обеспечивало бы оптимальную оценку значения измеряемой физической величины. Аналитическое представление такого преобразования называется алгоритмом обработки многократных измерений.
Исходными данными для построения алгоритма обработки многократных измерений являются: математическая модель измеряемой величины в виде
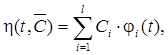
где Ci, i = 
– постоянные коэффициенты,
j i (t), i = – базисные функции,
tk, k =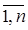 
– план измерений, и допущение о равноточности и некоррелированности многократных измерений.
3.2. Исходные данные и общие выражения для вектора оценки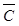 
и ковариационной матрицы 
Математическая модель измеряемой величины является параметрической и имеет следующий вид
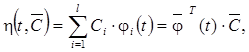
где 
– вектор коэффициентов,
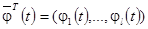– транспонированный вектор-столбец базисных функций.
План измерений задается и имеет следующую структуру: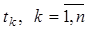 
– дискретные значения аргумента t, в которых производится однократное измерение функции отклика. Таким образом, объем многократных измерений по данному плану равно n = l. Предполагается, что многократные измерения являются равноточными и некоррелированными.
Из теории обработки многократных измерений известно, что оценка вектора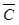 
представляется следующим выражением
, (3.1)
где
– вектор многократных измерений,
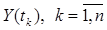– результат измерения при t = tk, k = 
,
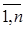– матрица базисных функций размера n ´ l, (3.2)
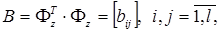
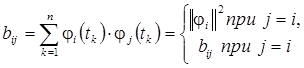(3.3)
где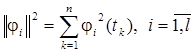 
– квадрат нормы базисной функции j i (t), соответствующий заданному плану измерений tk,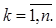 
– вектор-столбец размера l ´1.
Если план измерений таков, что 
при 
, то он называется ортогональным. Для такого плана измерений оценки коэффициентов имеют наиболее простой вид, а именно:
(3.4)
где 
– весовые коэффициенты (3.5)
Ковариационная матрица случайного вектора оценки (3.1) равна следующему выражению
Если план измерений ортогональный, то ковариационная матрица 
будет диагональной размера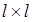 
.
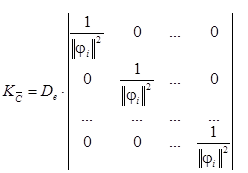
Для такой матрицы выражения для дисперсии оценок коэффициентов будут равны
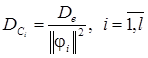(3.6)
А дисперсия оценки функции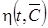 
примет следующий вид
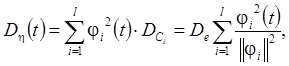(3.7)
где значение дисперсии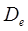 
берется равным значению, полученному по формуле (2.19).
3.3. Определение выражений для оценок коэффициентов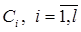 
И их дисперсии
В соответствии с заданием на интервале [0, Т ] оси абсцисс строится план измерений и соответствующие ему значения базисных функций. Затем, формируется матрица базисных функций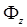 
, и на ее основе определяются элементы матрицы 
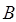согласно выражению (3.3). Результаты расчетов представляются матрицам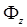и и 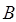. В силу того, что матрица 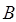является диагональной, то алгоритм определения оценок представляется уравнением (3.4) с весовыми коэффициентами, определяемыми выражениями (3.5).
Дисперсии оценок коэффициентов 
и оценки функции отклика (математической модели измеряемой величины) рассчитываются на основе выражений (3.6) и (3.7).
Пример 3.1. Пусть 
– математическая модель измеряемой величины x (t) и 
– план измерений, где n = 2,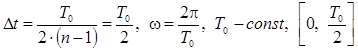 
– интервал планирования измерения.
Базисными функциями модели являются
Найдем элементы матрицы базисных функций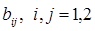 
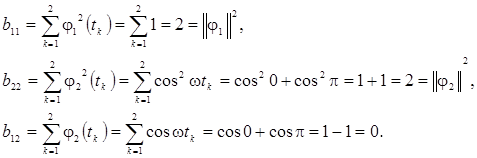
Таким образом, план измерений является ортогональным. Найдем выражения для оценок коэффициентов. Согласно выражению (3.5) получим
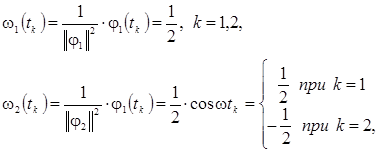
тогда будем иметь
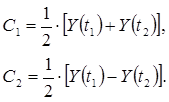
Найдем выражения для дисперсии оценок коэффициентов, используя уравнение (3.6)
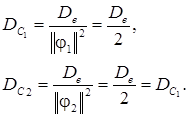
Дисперсия оценки математической модели будет равна (в соответствии с выражением (3.7)) 
Графическое изображение дисперсии показано на рис. 3.1
|
|
|
|
|
|
Рис. 3.1 - График дисперсии оценки математической модели 
Выполнение этого раздела завершается формулами для оценок Сi,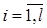 
и дисперсии 
и и графиком функции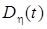 
.
СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ
1. Назаров, Н.Г. Современные методы и алгоритмы обработки измерений и контроля качества продукции [Текст]/ Н.Г. Назаров, Е.А. Архангельская: Учеб. пособие. – М.: Изд-во стандартов, 1995. – 163 с.
2. Яноши, Л. Теория и практика обработки результатов измерений [Текст]/ Л. Яноши. – М.: Мир, 1968. – 463 с.
3. Маркин, Н.С. Метрология. Введение в специальность [Текст]/ Н.С. Маркин, В.С. Ершов. – Учеб. пособие. – М.: Изд-во стандартов, 1991. – 208 с.
4. Назаров, Н.Г. Измерения: планирование и обработка результатов [Текст]/ Н.Г. Назаров. – М.: Изд-во стандартов, 2000. – 304 с.
5. Цветков, Э. И. Основы теории статистических измерений [Текст]/ Э.И. Цветков. – 2-е изд., перераб. и доп. – Л.: Энергоатомиздат, 1986. – 256 с.
ОГЛАВЛЕНИЕ
| Введение………………………………………………………………………. | |
| 1. Погрешность результата измерения……………………………………… | |
| 2. Расчет характеристик погрешности результата измерения……………. | |
| 2.1. Определение систематической погрешности результата измерения……………………………………………………………………… | |
| 2.1.1 Статический режим измерения………………………………………... | |
| 2.1.2. Динамический режим измерения…………………………………….. | |
| 2.2. Определение дисперсии случайной погрешности результата измерения……………………………………………………………………… | |
| 3. Разработка алгоритма обработки многократных измерений…………... | |
| 3.1 Многократные измерения и их обработка………………………………. | |
| 3.2. Исходные данные и общие выражения для вектора оценки 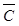и ковариационной матрицы ……………………………………………….
| |
| 3.3. Определение выражений для оценок коэффициентов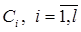
и их дисперсии………………………………………………………………
| |
| Список литературы…………………………………………………………… |
