МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ
ГОСУДАРСТВЕННОЕ ВЫСШЕЕ УЧЕБНОЕ ЗАВЕДЕНИЕ
ДОНЕЦКИЙ НАЦИОНАЛЬНЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Методические указания и задания
К лабораторным работам по курсам
“ ДИСКРЕТНЫЕ СТРУКТУРЫ“,
“ ТЕОРИЯ АЛГОРИТМОВ И ВЫЧИСЛИТЕЛЬНЫХ ПРОЦЕССОВ “
Донецк - 2009
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ
ГОСУДАРСТВЕННОЕ ВЫСШЕЕ УЧЕБНОЕ ЗАВЕДЕНИЕ
ДОНЕЦКИЙ НАЦИОНАЛЬНЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Методические указания и задания
к лабораторным работам
по курсам “Дискретные структуры”,
“ Теория алгоритмов и вычислительных процессов “
(для студентов, обучающихся по направлениям
“Программная инженерия”, “Компьютерные науки”)
Рассмотрено на заседании кафедры
прикладной математики и информатики
протокол № 14 от 29.06.09.
Утверждено на заседании
учебно-издательского совета ДонНТУ
протокол № 5 от 21.12.09
Донецк - 2009
УДК 004.021
Методические указания и задания к лабораторным работам по курсам “Дискретные структуры“, “Теория алгоритмов и вычислительных процессов“ (для студентов, обучающихся по направлениям “Программная инженерия”, “Компьютерные науки”) / разраб.: Назарова И.А., Коломойцева И.А. – Донецк: ДонНТУ, 2009 – 38с.
Изложенные теоретические основы, методические рекомендации, контрольные вопросы и задания для выполнения лабораторных работ по следующим разделам курса теории алгоритмов и вычислительных процессов:
- теория рекурсивных функций;
- машины Тьюринга;
- композиция машин Тьюринга;
- нормальные алгоритмы Маркова.
Составители: Назарова И.А., к.т. н., доцент
Коломойцева И.А., ст. преп.
Рецензент: Губенко Н.Е., к.т. н., доцент
Лабораторная работа №1
РЕКУРСИВНЫЕ ФУНКЦИИ
Цель работы: получить практические навыки в записи алгоритмов с использованием аппарата рекурсивных функций.
Теоретическая справка
Вычислимые функции – числовые функции, значения которых можно вычислять посредством единого для данной функции алгоритма.
Арифметические функции – функции, области определения и значений которых целые неотрицательные числа, то есть натуральный ряд + число ноль.
Частичные арифметические функции – арифметические функции с ограниченной областью определения, остальные – всюду определенными.
Примитивно-рекурсивные функции
В качестве простейших функций в теории рекурсивных функций приняты следующие:
1. 
– константа «ноль».
2. 
– «последователь».
3. 
– функция тождества или выбора аргумента, проекция.
Оператор суперпозиции (подстановки) 
– подстановка в функцию от 
переменных функций от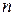 
переменных, что дает новую функцию от 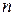переменных.
Суперпозицией функций 
и 
называют функцию:
;
.
Оператор примитивной рекурсии 
, определяющий значение функции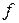 
, записывается в виде следующей схемы:
Частные случаи:
при n= 1 имеем 
,
при n= 2 имеем 
.
Примитивно-рекурсивная функция – арифметическая функция, которая может быть получена из простейших с помощью конечного числа применений операторов суперпозиции и примитивной рекурсии.
Примитивно-рекурсивные функции являются всюду определенными.
Пример 1. Вычислить функцию 
с помощью оператора примитивной рекурсии:
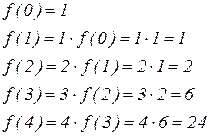
Пример 2. Вычислить функцию 
с помощью оператора примитивной рекурсии:
Для того чтобы показать, что какая-либо функция является примитивно-рекурсивной, достаточно построить ее согласно определению. Однако такое построение получается слишком сложным и громоздким. Поэтому в большинстве случаев заданную функцию пытаются выразить с помощью операторов суперпозиции и примитивной рекурсии через другие функции, примитивная рекурсивность которых доказана ранее. Приведем примеры доказательства примитивной рекурсивности некоторых простых арифметических функций.
Пример 3. Константа 1 может быть получена суперпозицией двух простейших функций: константы «ноль» и функции «последователь»:
Пример 4. Константа a получается суперпозиции функций 
и 
:
Пример 5. Операция сложения 
может быть определена с помощью оператора примитивной рекурсии:
Пример 6. Примитивная рекурсивность операции умножения 
доказывается через операцию сложение:
Пример 7. Примитивная рекурсивность операции возведения в степень 
доказывается следующим образом:
Пример 8. Операция вычитания не является примитивно-рекурсивной, т.к. она не всюду определена: результат операции a-b при 
не определен в области натуральных чисел. Однако примитивно-рекурсивной является так называемое арифметическое (усеченное) вычитание или разность.
Арифметическое вычитание:
Для доказательства примитивной рекурсивности 
вначале рассмотрим операцию 
: 
;
т.е. операция – примитивно-рекурсивна.
Дополнительное свойство: 
.
арифметическое вычитание – примитивно-рекурсивно.
Пример 9. Функция 
– аналог функции 
для натуральных чисел.
Функция примитивно-рекурсивна:
– антисигнум, функция обратная .
.
Пример 10. Примитивная рекурсивность функций 
, 
и модуль двух чисел доказывается с помощью арифметического вычитания:
