Для вычисления значений определённых интегралов существует множество методов. Рассмотрим три из них – метод прямоугольников, метод трапеций и метод парабол (метод Симпсона) на примерах при следующей постановке задачи. Составить фрагмент программы для вычисления приближенного значения определённого интеграла
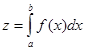
при заданных подынтегральной функции f(x), пределах интегрирования a и b и числе N разбиений интервала на подынтервалы. При этом шаг изменения аргумента Δx следует найти по формуле Δx=(b-a)/N.
Суть этих методов – в накоплении, с учетом знаков, сумм площадей прямоугольников, трапеций или параболических трапеций, заменяющих на каждом подынтервале в общем случае криволинейную трапецию. Для метода прямоугольников высоты таких прямоугольников следует вычислять как значение функции в серединах (или на границах) подынтервалов, для метода трапеций высоты сторон трапеций – как значения функции на границах подынтервала, а для метода Симпсона используются значения функций и на границах и в серединах подынтервалов. Соответствующие формулы в общем виде и фрагменты программ вычисления интегралов для подынтегральной функции sin x приведены в рассмотренных ниже примерах.
Пример 1. Использование метода прямоугольников с вычислением высот прямоугольников в серединах подынтервалов.
В этом методе формула приближенного значения определённого интеграла представляется в виде
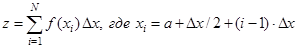
Для уменьшения объёма вычислений множитель Δx следует вынести за знак суммы:
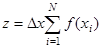, а для вычисления текущих значений центров xi подынтервалов будем использовать приём накопления суммы.
z:=0;
dx:=(b-a)/N;
x:=a+dx/2;//Середина первого подынтервала
for i:=1 to N do
begin
z:=z+Sin(x);
x:=x+dx
end;
z:=z*dx;
Пример 2. Использование метода трапеций.
В этом методе формула приближенного значения определённого интеграла представляется в виде
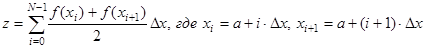
Преобразование её к виду
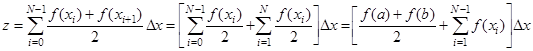
позволяет исключить повторные вычисления высот трапеций на внутренних подынтервалах и таким образом сократить объём вычислений.
z:=(Sin(a)+Sin(b))/2;
dx:=(b-a)/N;
x:=a+dx;
for i:=1 to N-1 do
begin
z:=z+Sin(x);
x:=x+dx
end;
z:=z*dx;
Пример 3. Использование метода параболических трапеций (Симпсона).
В этом методе формула приближенного значения определённого интеграла представляется в виде
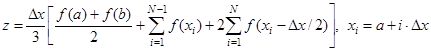
или, взяв N в 2 раза большим, то есть разбив весь интервал на четное количество участков, в 2 раза меньшей длины
.
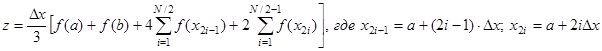Используем вторую формулу в следующем фрагменте программы.
ReadLn(a,b,N);
Integ:=Sin(a);
dx:=(b-a)/N;
for i:=1 to N div 2 do
begin
x:=a+2*i*dx;
Integ:=Integ+2*Sin(x)+4*Sin(x-dx);
end;
Integ:=(Integ-Sin(b))*dx/3;
WriteLn(Integ:10:5);
Itoch:=-(Cos(b)-Cos(a));
WriteLn(Itoch:10:5);
ReadLn;
