Явление рассеивания
При стрельбе из одного и того же оружия при самом тщатель-
ном соблюдении точности и однообразия производства выстре-
лов каждая пуля (граната) вследствие ряда случайных причин
описывает свою траекторию и имеет свою точку падения (точку
встречи), не совпадающую с другими, вследствие чего происходит
разбрасывание пуль (гранат).
Явление разбрасывания пуль (гранат) при стрельбе из одного и
того же оружия в практически одинаковых условиях называется ес-
тественным рассеиванием пуль (гранат) или рассеиванием траекторий.
Совокупность траекторий пуль (гранат), полученных вследст-
вие их естественного рассеивания, называется снопом траекторий
(рис. 21). Траектория, проходящая в середине снопа траекторий,
называется средней траекторией. Табличные и расчетные данные
относятся к средней траектории.
Точка пересечения средней траектории с поверхностью цели
(преграды) называется средней точкой попадания или центром рас-
сеивания.
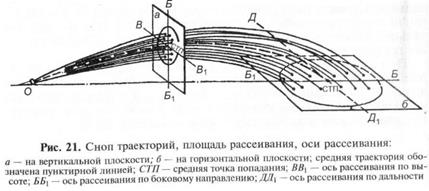
Площадь, на которой располагаются точки встречи (пробои-
ны) пуль (гранат), полученные при пересечении снопа траекто-
рий с какой-либо плоскостью, называется площадью рассеивания.
Площадь рассеивания обычно имеет форму эллипса. При стре-
льбе из стрелкового оружия на близкие расстояния площадь рас-
сеивания в вертикальной плоскости может иметь форму круга.
Взаимно перпендикулярные линии, проведенные через центр
рассеивания (среднюю точку попадания) так, чтобы одна из них
совпадала с направлением стрельбы, называются осями рассеива-
ния.
Кратчайшие расстояния от точек встречи (пробоин) до осей
рассеивания называются отклонениями.
Причины рассеивания
Причины, вызывающие рассеивание пуль (гранат), могут быть
сведены в три следующие группы:
причины, вызывающие разнообразие начальных скоростей;
причины, вызывающие разнообразие углов бросания и на-
правления стрельбы;
причины, вызывающие разнообразие условий полета пули
(гранаты).
Причинами, вызывающими разнообразие началь-
ных скоростей, являются:
разнообразие в массе пороховых зарядов и пуль (гранат), в
форме и размерах пуль (гранат) и гильз, в качестве пороха, в плот-
ности заряжания и так далее как результат неточностей (допус-
ков) при их изготовлении;
разнообразие температур зарядов, зависящее от температуры
воздуха и неодинакового времени нахождения патрона (гранаты)
в нагретом при стрельбе стволе;
разнообразие в степени нагрева и в качественном состоянии
ствола.
Перечисленные причины ведут к колебанию в начальных ско-
ростях, а следовательно, и в дальностях полета пуль (гранат), т. е.
приводят к рассеиванию пуль (гранат) по дальности (высоте) и за-
висят в основном от боеприпасов и оружия.
Причинами, вызывающими разнообразие углов
бросания и направления стрельбы, являются:
разнообразие в горизонтальной и вертикальной наводке ору-
жия (ошибки в прицеливании);
разнообразие углов вылета и боковых смещений оружия, полу-
чаeмое в результате неоднообразной изготовки к стрельбе, неу-
стойичивого и неоднообразного удержания автоматического ору-
жия, особенно во время стрельбы очередями, неправильного
использования упоров и неплавного спуска курка;
угловые колебания ствола при стрельбе автоматическим огнем,
возникающие вследствие движения и ударов подвижных частей и
отдачи оружия.
Эти причины приводят к рассеиванию пуль (гранат) но боко-
вому направлению и дальности (высоте), оказывают наибольшее
влияние на величину площади рассеивания и в основном зависят
от выучки стреляющего.
Причинами, вызывающими разнообразие условий
полета пули (гранаты), являются:
разнообразие в атмосферных условиях, особенно в направле-
нии и скорости ветра между выстрелами (очередями);
разнообразие в массе, форме и размерах пуль (гранат), приво-
дящее к изменению величины силы сопротивления воздуха.
Указанные причины приводят к увеличению рассеивания по
боковому направлению и по дальности (высоте) и в основном за-
висят от внешних условий стрельбы и от боеприпасов.
При каждом выстреле в разном сочетании действуют все три
группы причин. Это приводит к тому, что полет каждой пули
(гранаты) происходит по траектории, отличной от траекторий
других пуль (гранат).
Устранить полностью причины, вызывающие рассеивание, а
следовательно, устранить и само рассеивание невозможно. Одна-
ко, зная причины, от которых зависит рассеивание, можно умень-
шить влияние каждой из них и тем самым уменьшил, рассеива-
ние или, как принято говорить, повысить кучность стрельбы.
Уменьшение рассеивания пуль (гранат) достигается отличной
выучкой стреляющего, тщательной подготовкой оружия и бое-
припасов к стрельбе, умелым применением правил стрельбы,
правильной изготовкой к стрельбе, однообразной прикладкой,
точной наводкой (прицеливанием), плавным спуском курка,
устойчивым и однообразным удержанием оружия при стрельбе, а
также надлежащим уходом за оружием и боеприпасами.
Закон рассеивания
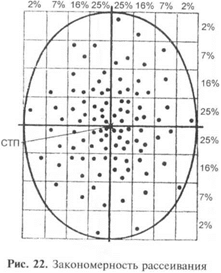
При большом числе выстрелов (более 20) в расположении то-
чек встречи на площади рассеивания наблюдается определенная
закономерность. Рассеивание пуль (гранат) подчиняется норма-
льному закону случайных ошибок, который в отношении к рассе-
иванию пуль (гранат) называется законом рассеивания. Этот закон
характеризуется следующими тремя положениями (рис. 22):
1. Точки встречи (пробоины) на площади рассеивания распо-
лагаются неравномерно — гуще к центру рассеивания и реже к
краям площади рассеивания.
2. На площади рассеивания можно определить точку, являющу-
юся центром рассеивания (средней точкой попадания), относите-
льно которой распределение
точек встречи (пробоин)
симметрично: число точек
нстречи по обе стороны от
осей рассеивания, заключа-
ющихся в равных по абсо-
лютной величине пределах
(полосах), одинаково, и каж-
дому отклонению от оси рас-
сеивания в одну сторону от-
вечает такое же по величине
отклонение в противополож-
ную сторону.
3. Точки встречи (пробои-
ны) в каждом частном случае
занимают не беспредельную,
а ограниченную площадь.
 Таким образом, закон
Таким образом, закон
рассеивания в общем виде
можно сформулировать так:
при достаточно большом чис-
щ' выстрелов, произведенных в практически одинаковых условиях,
риссеивание пуль (гранат) неравномерно, симметрично и небеспре-
дельно.
Определение средней точки попадания
При малом числе пробоин (до пяти) положение средней точки
попадания определяется способом последовательного деления от-
резков (рис. 23). Для этого необходимо:
соединить прямой две пробоины (точки встречи) и расстояние
между ними разделить пополам;
полученную точку соединить с третьей пробоиной (точкой
встречи) и расстояние между ними разделить на три равные час-
ти, так как к центру рассеивания пробоины (точки встречи) рас-
полагаются гуще, то за среднюю точку попадания трех пробоин
(точек встречи) принимается деление, ближайшее к двум первым
пробоинам (точкам встречи);
найденную среднюю точку попадания для трех пробоин (точек
встречи) соединить с четвертой пробоиной (точкой встречи) и
расстояние между ними разделить на четыре равные части; деле-
ние ближайшее к первым трем пробоинам (точкам встречи),
принимается за среднюю точку попадания четырех пробоин (то-
чек нстречи).
По четырем пробоинам (точкам встречи) среднюю точку попа-
дания можно определить еще так: рядом лежащие пробоины (точ-
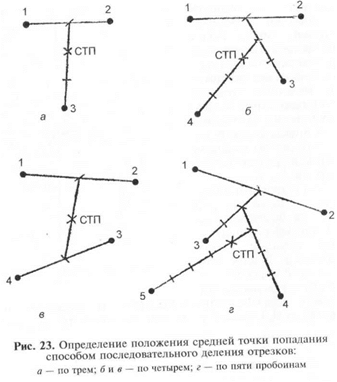
ки встречи) соединить попарно, середины обеих прямых снова
соединить и полученную линию разделить пополам; точка деле-
ния и будет средней точкой попадания.
При наличии пяти пробоин (точек встречи) средняя точка по-
падания для них определяется подобным образом.
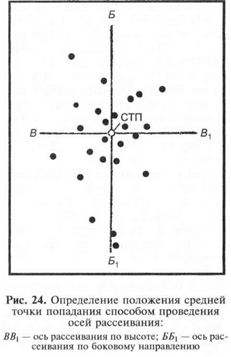
При большом числе пробоин (точек встречи) на основании
симметричности рассеивания средняя точка попадания определя-
ется способом проведения осей рассеивания (рис. 24).
Для этого нужно:
отсчитать нижнюю (ближнюю) половину пробоин (точек
встречи) и отделить ее осью рассеивания по высоте (дально-
сти);
отсчитать таким же порядком или левую половину пробоин
(точек встречи) и отделить ее осью рассеивания по боковому на-
правлению;
пересечение осей рассеивания является средней точкой попа-
дания.
 Среднюю точку попада-
Среднюю точку попада-
ния можно также опреде-
нить способом вычисления
(расчета). Для этого необхо-
димо:
провести через левую
(правую) пробоину (точку
нстречи) вертикальную ли-
нию, измерить кратчайшее
расстояние от каждой про-
ооины (точки встречи) до
ной линии, сложить все
расстояния от вертикаль-
ной линии и разделить сум-
му на число пробоин (точек
нстречи);
провести через нижнюю
мн-рхнюю) пробоину (точку
нстречи) горизонтальную
линию, измерить кратчай-
шее расстояние от каждой
пробоины (точки встречи)
до этой линии, сложить все
расстояния от горизонталь-
ной линии и разделить сум-
му на число пробоин (точек встречи).
Полученные числа определяют удаление средней точки попа-
дания от указанных линий.
Меры рассеивания и зависимость между ними
В любых условиях стрельбы закономерность рассеивания оста-
ется неизменной, но величина площади рассеивания изменяется
в зависимости от выучки стреляющего, вида оружия, боеприпа-
сов прицельных приспособлений, положения для стрельбы, да- льности стрельбы, метеорологических и других условий стрельбы.
Для измерения величины площади рассеивания, сравнения
рассеивания пуль (гранат) разных видов оружия, а также для
оцеики рассеивания пуль (гранат) одного и того же оружия при
различныхусловиях стрельбы могут применяться следующие
меры (единицы измерения) рассеивания: срединное отклонение,
сердцевинная полоса и радиус круга, вмещающего лучшую поло-
вину попаданий или все попадания.
Срединным отклонением называется такое отклонение, которое
в ряду всех отклонений, выписанных по абсолютной величине в
возрастающем или убывающем порядке, занимает среднее место.
Срединное отклонение является основной мерой рассеивания.
Оно обычно обозначается: Вя — срединное отклонение по дально-
сти; Вв — срединное отклонение по высоте; В6 — срединное от-
клонение по боковому направлению.
Для определения величины срединного отклонения по одному
из направлений необходимо выписать все отклонения в ряд в воз-
растающем или убывающем порядке по абсолютной величине.
Отклонение, стоящее посредине этого ряда, и будет являться сре-
динным отклонением.
Если ряд всех отклонений состоит из четного числа отклоне-
ний, то для определения величины срединного отклонения нужно
взять два отклонения, стоящие посредине, и разделить сумму их
абсолютных величин на два.
Среднее арифметическое значение определяется делением
суммы абсолютных значений всех отклонений на количество от-
клонений.
В этих случаях учитываются численные значения всех откло-
нений и результаты отдельных отклонений не сказываются так
значительно на величине срединного отклонения.
Срединное отклонение может быть вычислено также с помо-
щью среднего квадратического значения. Срединное отклонение
равно 0,67, или округленно 2/3, среднего квадратического значе-
ния.
Среднее квадратическое значение при небольшом числе от-
клонений равно корню квадратному из суммы квадратов отклоне-
ний, деленной на число всех отклонений без одного.
Если от той или иной оси рассеивания отложить в обе стороны
последовательно полосы, равные по ширине соответствующему
срединному отклонению, то вся площадь рассеивания окажется
разделенной на восемь равных полос — по четыре в каждую сто-
рону, а полное рассеивание по любому направлению будет равно
восьми срединным отклонениям.
В действительности могут быть отклонения от центра рассеи-
вания, превышающие четыре срединных отклонения, но вероят-
ность получения их мала (не превышает 0,7 %).
При большом числе выстрелов в каждой из полос, равной по
ширине одному срединному отклонению или его части, незави-
симо от величины рассеивания содержится определенный про-
цент точек встречи (попаданий).
Чертеж, показывающий процентное распределение попаданий
в полосы, равные по ширине одному срединному отклонению
или его части, называется шкалой рассеивания (рис. 25). Шкала
рассеивания в численном выражении одинакова по любому на-
правлению и характеризует закон рассеивания.

Для полос шириной в одно срединное отклонение содержится
(округленно): в первмх полосах, примыкающих к оси рассеива-
ния, по 25 % точек встречи, во вторых — по 16 %, в третьих — по
7 % и в крайних — по 2 %.
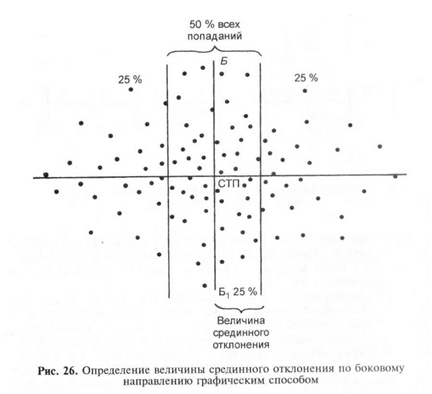
При большом числе попаданий (точек встречи) величину сре-
дииного отклонения можно определить графическим способом
(рис. 26). Для этого отсчитывают справа (сверху) 25 % попаданий
(точек встречи) и отделяют их вертикальной (горизонтальной) ли-
нией; отсчитывают слева (снизу) 25 % попаданий (точек встречи)
и также отделяют их вертикальной (горизонтальной) линией.
В результате этого получится полоса, вмещающая 50 % попада-
ний (точек встречи), т. е. полоса лучшей половины попаданий.
Затем измеряют расстояние между вертикальными (горизонталь-
ными) иниями. Половину расстояния между вертикальными
(тризонтальными) линиями принимают за величину срединного
отклонения. В связи с этим иногда пользуются другим определе-
нием срединного отклонения: срединным отклонением называется
половина ширины центральной полосы рассеивания, вмещаю-
щей 50 % всех попаданий, при условии, что ось рассеивания про-
ходит по ее середине.
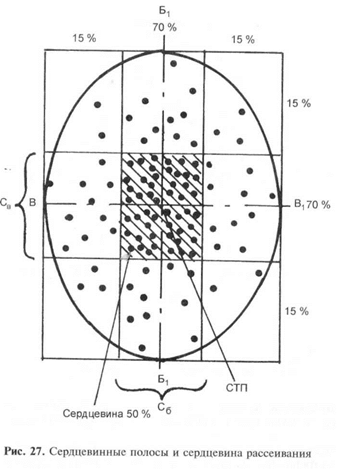
Полоса рассеивания, содержащая в себе 70 % попаданий (то-
чек встречи), при условии, что ось рассеивания проходит по ее се-
редине, называется сердцевинной полосой (рис. 27).
Сердцевинные полосы обозначаются: Сд — сердцевинная по-
юса по дальности; Св — сердцевинная полоса по высоте; С6 —
сердцевинная полоса по боковому направлению.
При пересечении двух сердцевинных полос образуется прямо-
угольник, включающий в себя лучшую, наиболее кучную половину
всех точек встречи (0,70 • 0,70 = 0,49, округленно 0,50, или 50 %).
Прямоугольник, образуемый пересечением двух сердцевинных
Полос, называется сердцевиной рассеивания.
ирина сердцевинной полосы может быть определена графи-
ческим способом (рис. 28). Для этого надо отсчитать справа
(сверху) 15 % попаданий (точек встречи) и провести вертикаль-
ную (горизонтальную) линию; отсчитать слева (снизу) 15 % попа-
даний (точек встречи) и также провести вертикальную (горизон-
тальную) линию. В результате этого вся площадь рассеивания
окажется разделенной на три почти равные полосы, при этом
центральная полоса содержит 70 % попаданий, а крайние — по
15 % каждая. Затем следует измерить расстояние между вертика-
льными (горизонтальными) линиями, которое и будет равно ши-
рине сердцевинной полосы.
Между сердцевинной полосой и срединным отклонением
как мерами рассеивания имеется определенная зависимость.
Сердцевинная полоса включает в себя 3,06 соответствующего
срединного отклонения. На практике ширину сердцевинной
полосы принимают округленно равной трем срединным откло-
нениям.
При стрельбе на близкие расстояния площадь рассеивания на
вертикальной плоскости имеет форму круга, что означает при-
мерное равенство характеристик рассеивания по высоте и по бо-
ковому направлению. Поэтому о величине такого рассеивания
иногда судят не по двум характеристикам (Вви В6 или Св и Q), а
по одной величине — радиусу крута, вмещающего лучшую поло-
вини иу (Р50) всех попаданий или все (Рт) попадания.
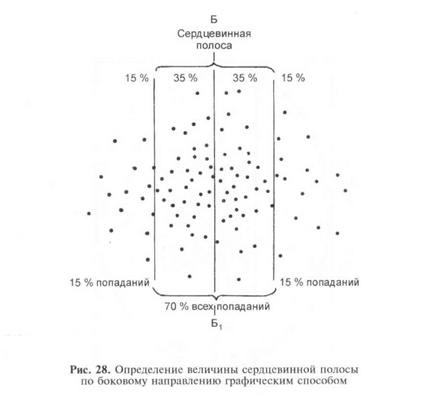
Для определения величины радиуса круга, включающего 50 %
Или 100 % попаданий, необходимо определить среднюю точку по-
падания (рис. 29). Затем, принимая среднюю точку попадания за
центр круга, провести циркулем окружность так, чтобы она вмес-
тила половину (50 %) или все (100 %) точки встречи. Раствор цир-
куля дает в первом случае величину радиуса круга, включающего
50%, а во втором — 100 % попаданий.
Радиус круга, вмещающего все попадания, примерно в 2,5 раза
больше радиуса круга, вмещающего лучшую половину попада-
ний.
Между величиной радиуса круга, вмещающего лучшую поло-
вину попаданий, срединными отклонениями и сердцевинными
полосами имеется определенная зависимость. Радиус круга, вме-
щающего лучшую половину попаданий (50 %), равен 1,76 средин-
ного отклонения, или 0,6 сердцевинной полосы.
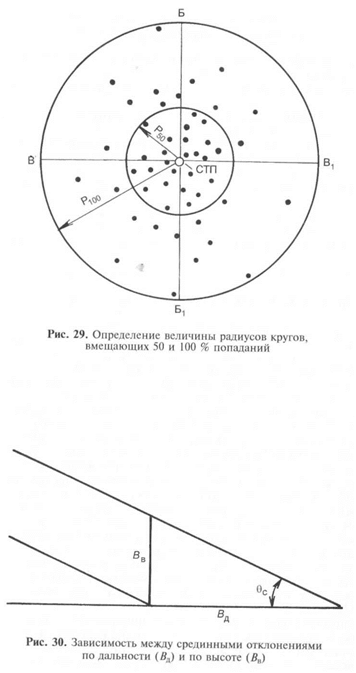
Между величинами рассеивания по дальности и по высоте
имеется определенная зависимость: рассеивание по дальности
равно рассеиванию по высоте, умноженному на 1000 и разделен-
ному на величину угла падения в тысячных (рис. 30).
При стрельбе одиночными выстрелами рассеивание пуль (гра-
нат) подчиняется вышеизложенному закону рассеивания.
Характер и величина рассеивания при стрельбе одиночными
выстрелами могут определяться срединным (вероятным) откло-
нением рассеивания пуль, сердцевинной полосой, радиусом кру-
га, вмещающего все или лучшую половину попаданий. Эти меры
рассеивания приводятся в таблицах стрельбы.
Характер рассеивания при стрельбе
автоматическим огнем (очередями)
При стрельбе автоматическим огнем (очередями) рассеивание
характеризуется:
а) из станковых и ротных пулеметов и ручного пулемета с со-
шки:
рассеиванием отдельных пуль в очереди относительно средней
точки попадания очереди;
рассеиванием средних точек попадания отдельных очередей;
полным (суммарным) рассеиванием;
б) из автомата со всех положений для стрельбы и из ручного
пулемета из положения с колена, стоя и на ходу с короткой оста-
новки:
рассеиванием первых пуль очередей;
рассеиванием последующих пуль очередей;
рассеиванием средних точек попадания последующих пуль
очередей;
полным (суммарным) рассеиванием последующих пуль очере-
дей.
Каждая из этих характеристик подчиняется закону рассеива-
ния.
Первые выстрелы очередей происходят в тех же условиях, что
и при стрельбе одиночными выстрелами, и их рассеивание возни-
кает в результате действия вышерассмотренных причин.
После первого выстрела в результате воздействия на оружие
силы отдачи и силы реакции на отдачу (мускульного воздействия
стреляющего из ручного оружия или при стрельбе из оружия на
станке — механических связей станка) произойдет перемещение
оружия. Время между выстрелами при ведении автоматического
огня из стрелкового оружия составляет около 0,1 с; стреляющий
не в состоянии за это время восстановить наводку перед вторым
выстрелом. Поэтому положение оружия при втором выстреле бу-
дет определяться положением его перед первым выстрелом и сум-
марным действием силы отдачи, движения и ударов подвижных
частей оружия и силы реакции после первого выстрела. Точно так
же при третьем выстреле положение оружия будет зависеть от его
положения перед вторым выстрелом и суммарного действия ука-
занных сил после второго выстрела. Таким образом, на результат
каждого последующего выстрела, кроме причин, вызывающих
рассеивание первых пуль очереди, оказывает влияние предыду-
щий выстрел и все это приводит к рассеиванию пуль в очереди
(рис. 31).
Величина силы отдачи и ударов подвижных частей при всех
выстрелах практически одинакова, а силы реакции, как правило,
различны. Это различие оказывает основное влияние на величину
рассеивания очереди. Отсюда следует, что, чем устойчивее поло-
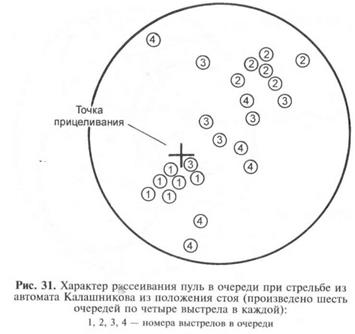
жение стреляющего при ведении огня из ручного оружия и выше
его натренированность в удержании оружия, тем однообразнее
будут силы реакции при различных выстрелах и тем меньше будет
рассеивание пуль в очереди.
В стрелковом оружии на станках при правильной установке
его на огневой позиции реакции отдачи более стабильны от вы-
стрела к выстрелу, поэтому рассеивание пуль в очереди меньше,
чем при стрельбе из ручного оружия.
Ошибки прицеливания, неоднообразие прикладки и удержа-
ния оружия, различие метеорологических условий при переходе
от стрельбы одной очередью к другой являются ошибками для
всех пуль очереди и вызывают рассеивание средних точек попада-
ния отдельных очередей (рис. 32).
При стрельбе очередями из автомата, а также из ручного пуле-
мета с колена, стоя и на ходу с короткой остановки вследствие
отсутствия устойчивого положения (жесткой опоры для противо-
действия отдаче) происходит систематическое смещени последу-
ющих пуль в очереди относительно первой и характеристики рас-
сеивания последующих пуль значительно больше характеристик
рассеивания первых пуль. В связи с этим при оценке такого рас-
сеивания отдельно рассматриваются характеристики рассеивания
первых пуль очередей, последующих пуль очередей, а также на-
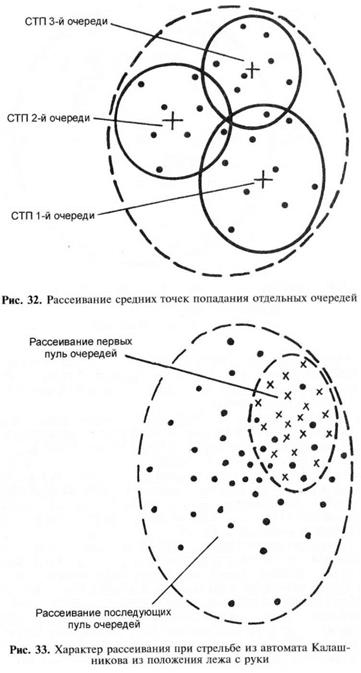
равление и величина систематического смещения средней точки
попадания последующих пуль очередей относительно первых
нуль очередей (рис. 33). При этом в мерах рассеивания последую-
щих пуль очередей отдельно приводятся характеристики рассеи-
вания пуль, средних точек попадания и полного (суммарного)
рассеивания.
Направление и величина смещения средней точки попадания
последующих пуль очередей относительно первых пуль очередей
зависят от вида оружия и положения для стрельбы. Так, напри-
мер, при стрельбе из автомата Калашникова лежа с упора или
стоя из окопа смещение средней точки попадания последующих
пуль относительно первых пуль у большинства стреляющих про-
исходит на 1,5 тысячных влево и на 1,5 тысячных вниз, а при
стрельбе из ручного пулемета Калашникова из положения с коле-
па, стоя и на ходу с короткой остановки — на 3 тысячных вправо
и на 3 тысячных вверх.
При стрельбе из крупнокалиберных пулеметов характер рассе-
ивания пуль зависит от положения ствола относительно плоско-
сти симметрии станка и способа стрельбы.
Если стрельба ведется в направлении плоскости симметрии
станка при закрепленных механизмах, что является наиболее
устойчивым положением, рассеивание имеет примерно такой же
чарактер, как и при стрельбе из станковых пулеметов.
Если стрельба ведется под углом к плоскости симметрии стан-
ка с закрепленными механизмами или в любом направлении с от-
крепленными механизмами, то вследствие меньшей устойчивости
оружия рассеивание имеет примерно такой же характер, как и
при стрельбе из автомата.
Полное (суммарное) рассеивание пуль определяется по следу-
ющим формулам:

При стрельбе автоматическим огнем ошибка, например в при-
целивании, может привести к тому, что пули всей очереди (неско-
льких очередей) пролетят мимо цели. Такое явление, когда поло-
жение всех пуль очередей зависит от какой-то общей ошибки,
называется зависимостью выстрелов.
Величина зависимости выстрелов определяется по формуле
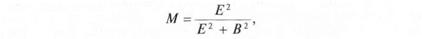
где М — мера зависимости выстрелов, она изменяется от 0 до 1;
Е — срединная ошибка подготовки стрельбы;
В — срединное отклонение рассеивания пуль в очереди.
Если общая ошибка равна нулю, то выстрелы будут независи-
мы (М= 0). Такое явление обычно наблюдается при стрельбе оди-
ночными выстрелами, когда стреляющий уточняет наводку перед
каждым выстрелом и, следовательно, положение последующих
пуль не зависит от положения предыдущих пуль.
При увеличении общей ошибки и уменьшении рассеивания
пуль в очереди зависимость выстрелов усиливается (рис. 34) и это
приводит к нежелательным результатам стрельбы.
Зависимость выстрелов может быть уменьшена путем умень-
шения общей ошибки или увеличения рассеивания пуль в очере-
ди. Исходя из этого, например, правилами стрельбы из станковых
пулеметов рекомендуется огонь по внезапно появляющимся це-
лям на неизмеренных расстояниях вести с открепленными меха-
низмами или с незначительным рассеиванием пуль по фронту
(глубине) цели, в этом случае увеличенное рассеивание будет до
некоторой степени компенсировать ошибки в подготовке исход-
ных данных и в прицеливании. На этом же основании для повы-
шения результатов стрельбы рекомендуется ведение сосредото-
ченного огня из нескольких видов (образцов) оружия по одной
цели. Рассеивание пуль при ведении сосредоточенного огня (при
стрельбе подразделением) увеличивается примерно в 1,5 раза, и
ошибки одного стреляющего компенсируются рассеиванием пуль
при стрельбе других стреляющих.
Зависимость выстрелов учитывается при определении дейст-
вительности стрельбы в различных условиях.
Зависимость характера и величины рассеивания
от условий стрельбы
Величины мер рассеивания, указанные в таблицах стрельбы,
соответствуют опытным полигонным стрельбам и характеризуют
рассеивание при нормальных условиях. При стрельбе в условиях,
наличных от нормальных, характер и величины мер рассеивания
изменяются.
Рассеивание, относящееся к определенному времени и услови-
ям стрельбы, называется рассеиванием данного момента. Опытные
данные показывают, что величины мер рассеивания данного мо-
мента могут быть в 1 ,5—2 раза больше или меньше табличных.
Рассеивание данного момента учитывается при разработке пра-
вил стрельбы, курсов стрельб и норм расхода боеприпасов для по-
ражения различных целей, когда все расчеты производятся не то-
лько для средних, но и для лучших и худших условий.
При стрельбе из стрелкового оружия рассеивание по высоте ипо боковому направлению увеличивается с увеличением дально-
сти стрельбы.
Рассеивание по дальности с увеличением дальности стрельбы
сначала возрастает, достигая наибольшего значения при опреде-
ленных дальностях для каждого вида оружия, а затем постепенно
уменьшается. Такой характер изменения рассеивания объясняет -
ся чем, что рассеивание по дальности зависит от двух факторов:
рассеивания по высоте и угла падения. С увеличением дальности
стрельбы величина обоих этих факторов возрастает. Величина
рассеивания по дальности будет зависеть от того, что быстрее уве-
личивается. Если быстрее возрастает угол падения, то рассеива-
ние по дальности уменьшается, и, наоборот, если быстрее возрас-
тает рассеивание по высоте, то рассеивание по дальности
увеличивается.
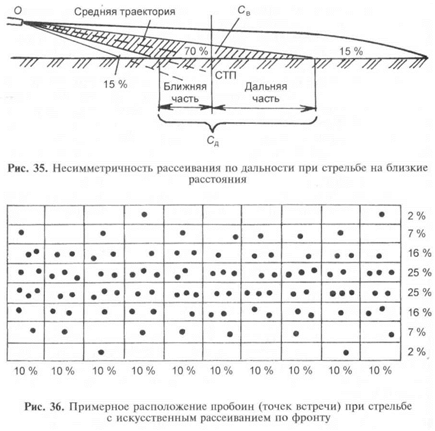
При стрельбе из стрелкового оружия на близкие расстояния
наблюдается несимметричность рассеивания по дальности, кото-
рая объясняется настильностью траекторий. Вследствие большой
настильности траекторий и значительной разницы в углах встре-
чи ближней и дальней частей площади рассеивания симметрич-
ный по высоте сноп траекторий (рис. 35) образует на горизонта-
льной поверхности несимметричную по размерам площадь
рассеивания: ближняя часть площади рассеивания, лежащая пе-
ред средней точкой попадания, меньше (короче) дальней, лежа-
щей за средней точкой попадания. В соответствии с этим полосы
срединных отклонений, а также ближняя и дальняя части сердце-
винной полосы рассеивания оказываются по размерам неравны-
ми. Расположение точек встречи в этих полосах в процентном от-
ношении соответствует закону рассеивания.
Величина и характер рассеивания при стрельбе из стрелкового
автоматического оружия зависят от выучки стреляющего, положе-
ния для стрельбы и способа ведения огня. В связи с этим в Табли
цах стрельбы по наземным целям из стрелкового оружия калибра
7,62 мм № 61, изд. 1962 г., даются характеристики рассеивания для
пучших и средних автоматчиков (пулеметчиков), коэффициенты,
показывающие, во сколько раз увеличиваются характеристики
рассеивания при изменении положения для стрельбы из автоматов
и ручных пулеметов (при стрельбе из положения лежа с руки, с ко-
пена, стоя, на ходу с короткой остановки) и при изменении спосо-
ба ведения огня из станкового пулемета (при стрельбе с откреплен-
ными механизмами, с рассеиванием пуль по фронту).
При стрельбе с искусственным рассеиванием по фронту (в глу-
бину) точки встречи располагаются более или менее равномерно
по фронту (в глубину), а расположение их по высоте (боковому
направлению) соответствует закону рассеивания (рис. 36). При
одновременном искусственном рассеивании в обоих направлени-
ях точки встречи располагаются более или менее равномерно по
псей площади.
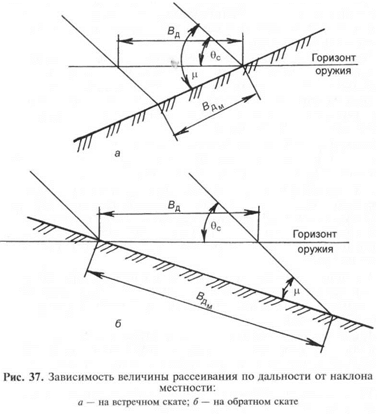
При стрельбе из стрелкового оружия по скатам, обращенным в
сторону оружия, рассеивание по дальности уменьшается, а при
стрельбе по обратным скатам увеличивается (рис. 37).
Рассеивание по дальности на наклонной местности во столько
раз меньше (больше) табличного, во сколько раз угол встречи бо-
льше (меньше) угла падения.
При стрельбе в условиях ограниченной видимости (ночью, в
дыму, в пыли, в тумане и т. п.) видимость целей резко снижается;
при стрельбе с бронетранспортера из-за вибрации (колебания)
его строений затрудняется прицеливание. Все это влечет за собой
увеличение ошибок в наводке (прицеливании), а следовательно, и
увеличение рассеивания пуль.
Меткость стрельбы и поражаемая зона
Меткость стрельбы определяется точностью совмещения сред-
ней точки попадания с намеченной точкой на цели и величиной
рассеивания. При этом, чем ближе средняя точка попадания к на-
меченной точке и чем меньше рассеивание пуль (гранат), тем луч-
ше меткость стрельбы.
Стрельба признается меткой, если средняя точка попадания
отклоняется от намеченной точки на цели не более чем на поло-
вину тысячной дальности стрельбы, что соответствует допустимо-
му отклонению средней точки попадания от контрольной точки
при приведении оружия к нормальному бою, а рассеивание не
превышает табличных норм.
Меткость стрельбы обеспечивается точным приведением ору-
жия к нормальному бою, тщательным сбережением оружия и бое-
припасов и отличной выучкой стреляющего.
Для улучшения меткости стрельбы стреляющий должен уметь
определять расстояние до цели, учитывать влияние метеорологи-
ческих условий на полет пули (гранаты) и соответственно им вы-
бирать установки прицела, целика и точку прицеливания, прави-
льно выполнять приемы стрельбы, тщательно сберегать оружие и
боеприпасы.
Основными причинами, снижающими меткость стрельбы, яв-
ляются ошибки стреляющего в выборе точки прицеливания, уста-
новки прицела и целика, в изготовке, в наводке оружия и в произ-
водстве стрельбы.
При неправильной установке прицела и целика, а также не-
правильном выборе точки прицеливания пули (гранаты) будут пе-
релетать цель (не долетать до цели) или отклоняться в сторону от
нее.
При сваливании оружия средняя точка попадания отклоняется
в сторону сваливания оружия и вниз.
При расположении упора впереди центра тяжести оружия
(ближе к дульному срезу) средняя точка попадания отклоняется
иверх, а при расположении упора сзади центра тяжести оружия
(ближе к прикладу) отклоняется вниз; изменение положения упо-
ра во время стрельбы приводит к увеличению рассеивания.
Если приклад упирается в плечо нижним углом, то средняя
точка попадания отклоняется вверх, а если верхним углом, то она
отклоняется вниз.
При крупной мушке (мушка выше краев прорези прицела)
средняя точка попадания отклоняется вверх, а при мелкой муш-
ке — вниз; мушка, придержанная к правой стенке прорези прице-
ла, приводит к отклонению средней точки попадания вправо, а
мушка, придержанная клевой стенке прорези прицела, приводит
к отклонению ее влево. Неоднообразное прицеливание приводит
к увеличению рассеивания пуль (гранат).
Неплавный спуск курка (дерганье) влечет за собой, как прави-
ло, отклонение средней точки попадания вправо и вниз.
Меткость стрельбы снижается из-за различных неисправно-
стей оружия и боеприпасов. Так, например, при погнутости при-
цельной планки (рамки) и ствола средняя точка попадания откло-
няется в сторону погнутости; при погнутости мушки и забоинах
на дульном срезе средняя точка попадания отклоняется в сторо-
ну, противоположную погнутести (забоине). При боковой качке
прицела, поражении и растертое™ канала ствола вследствие не-
правильной чистки оружия, качке ствола, штыка, станка, сошки
и лак далее увеличивается рассеивание пуль и изменяется положе-
ние средней точки попадания. Различие характеристик массы
боеприпасов влияет на меткость стрельбы, изменяя положение
средней точки попадания и увеличивая рассеивание пуль.
На меткость стрельбы оказывают влияние освещение и метео-
рологические условия. Например, если солнце светит с правой
стороны, то на правой стороне мушки получается отблеск, кото-
рый стреляющий при прицеливании принимает за сторону муш-
ки; при этом мушка будет отклонена влево, отчего и пули откло-
нятся влево. Боковой ветер, дующий справа, отклоняет пулю
влево, а ветер слева — в правую сторону.
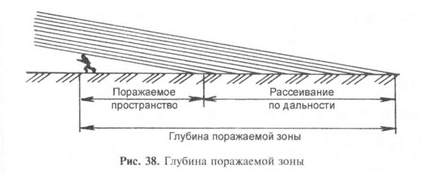
Пространство, в пределах которого может быть поражена цель
определенной высоты при стрельбе на одних и тех же установках
прицельных приспособлений, называется поражаемой зоной.
Глубина поражаемой зоны на горизонтальной плоскости при
стрельбе из стрелкового оружия складывается из полного рассеи-
вания по дальности и поражаемого пространства для данной цели
(рис. 38). Ширина поражаемой зоны равна величине полного рас-
сеивания по боковому направлению.
Глубина поражаемой зоны на наклонной местности во столько
раз меньше (больше), чем на горизонтальной плоскости, во ско-
лько раз угол встречи больше (меньше) угла падения.
Глава 4
Действительность стрельбы
Понятие о действительности стрельбы
При стрельбе из стрелкового оружия и гранатометов в зависи-
мости от характера цели, расстояния до нее, способа ведения
огня, вида боеприпасов и других факторов могут быть достигнуты
различные результаты. Для выбора наиболее эффективного в дан-
ных условиях способа выполнения огневой задачи необходимо
произвести оценку стрельбы, т. е. определить ее действитель-
ность.
Действительностью стрельбы называется степень соответствия
результатов стрельбы поставленной огневой задаче. Она может
быть определена заранее расчетным путем или по результатам
опытных стрельб.
Зпание закономерностей и характеристик рассеивания, воз-
можных ошибок в подготовке исходных данных и некоторых дру-
гих условий стрельбы позволяет определить заранее расчетным
путем ожидаемые результаты стрельбы.
Для оценки возможных результатов стрельбы из стрелкового
оружия и гранатометов обычно принимаются следующие показа-
тели:
вероятность поражения одиночной цели (состоящей из одной
Фш уры);
математическое ожидание числа (процента) пораженных фи-
гур в групповой цели (состоящей из нескольких фигур);
математическое ожидание числа попаданий;
средний ожидаемый расход патронов (гранат) для достижения
необходимой надежности стрельбы;
средний ожидаемый расход времени на выполнение огневой задачи.
Кроме того, при оценке действительности стрельбы учитыва-
ется степень убойного и пробивного действия пули (гранаты).
Убойность пули характеризуется ее энергией в момент встречи
с целью. Для нанесения поражения человеку (вывода его из
строя) достаточна энергия, равная 10 кгс-м. Пуля стрелкового
ружия сохраняет убойность практически до предельной дально-
сти стрельбы.
Пробивное действие пули (гранаты) характеризуется ее способ-
ностью пробить преграду (укрытие) определенной плотности и
толщины. Пробивное действие пули указывается в наставлениях
по стрелковому делу для каждого вида оружия. Кумулятивная гра-
ната к гранатометам пробивает броню любого современного танка,
самоходной артиллерийской установки, бронетранспортера.
При определении действительности стрельбы опытным путем
обычно учитывается количество (процент) попаданий в одиноч-
ную цель, количество (процент) пораженных фигур в групповой
цели, степень пробивного или убойного действия пули (гранаты),
расход боеприпасов и времени на стрельбу или на поражение од-
ной цели (фигуры).
Для расчета показателей действительности стрельбы необходи-
мо знать характеристики рассеивания пуль (гранат), ошибки в
подготовке стрельбы, а также способы определения вероятности
попадания в цель и вероятности поражения целей.
К ошибкам в подготовке стрельбы относятся ошибки в техни-
ческой подготовке оружия (в приведении его к нормальному бою,
выверке прицельных приспособлений, допуски в изготовлении
механизмов и т. д.) и ошибки в подготовке исходных установок
для стрельбы (в определении расстояния до цели, в учете попра-
вок на отклонение условий стрельбы от нормальных, в округле-
ниях при назначении установок и т. д.).
Если значение измеряемой величины неизвестно, то за неизве-
стное истинное значение измеряемой величины принимают сред-
ний результат отдельных измерений.
Средним результатом называется частное от деления суммы ре-
зультатов измерений, взятых с их знаками, на число измерений.
Ошибки могут быть положительными, если измеренная вели-
чина больше истинной, и отрицательными, когда измеренная ве-
личина меньше истинной.
Ошибки могут быть систематическими и случайными.
Систематические (постоянные) ошибки вызываются постоян-
но действующими причинами, оказывают одинаковое влияние на
все измерения и могут быть учтены. Например, вследствие сме-
щения на автомате Калашникова мушки влево на 0,5 мм пули при
дальности стрельбы на 100 м отклоняются отточки прицеливания
вправо на 13 см. Достаточно передвинуть мушку вправо на 0,5 мм,
и ошибка будет устранена.
Случайными называются такие ошибки, которые являются ре-
зультатом действия большого числа источников ошибок и при
каждом новом измерении (испытании) получают новые, случай-
ные значения. Случайные ошибки невозможно учесть и нельзя
ввести заблаговременно поправки на их устранение. Примером
действия случайных ошибок является рассеивание пуль (гранат).
В распределении или частоте появления случайных ошибок
при большом числе измерений (испытаний) проявляется опреде-
ленная закономерность, которую принято называть нормальным
законом случайных ошибок. Эта закономерность выражается сле-
дующими основными положениями.
При достаточно большом числе измерений (испытаний) ошиб-
ки измерений появляются: неравномерно — меньшие ошибки по-
являются чаще, а большие — реже; симметрично — число положи-
тельных и отрицательных ошибок, заключенных в равных по
величине пределах, одинаково, и каждой положительной ошибке
соответствует отрицательная ошибка, равная ей по абсолютной
величине-; небеспредельно — для каждого способа измерения су-
ществует предел величины ошибок, больше которого ошибки
практически не могут быть.
В стрелковой практике для суждения о точности измерения
принята срединная ошибка, так как она наглядно (численно) ха-
рактеризует нормальный закон случайных ошибок.
Срединной ошибкой называется такая ошибка, которая по
своей абсолютной величине (независимо от знака) больше каж-
дой из ошибок одной половины их и меньше каждой из ошибок
другой половины ошибок, выписанных в возрастающем или убы-
вающем порядке.
Для определения величины срединной ошибки необходимо
выписать все ошибки в ряд в" возрастающем или убывающем по-
рядке по абсолютной величине и отсчитать половину ошибок
справа или слева. Ошибка, стоящая посредине этого ряда, и будет
срединной ошибкой.
Если ряд состоит из четного числа ошибок, то для определе-
ния величины срединной ошибки надо взять две ошибки, стоя-
щие посредине, и разделить сумму их абсолютных величин на
два.


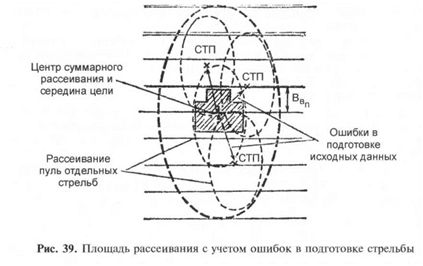
Ошибки в подготовке стрельбы приводят к отклонению сред-
ней траектории от середины цели (намеченной точки). Эти от-
клонения случайные как по направлению, так и по величине, од-
нако они подчиняются тем же закономерностям, что и
отклонение пуль (гранат) из-за рассеивания. Общая (суммарная)
площадь разброса пуль (гранат) будет определяться рассеиванием
и возможными отклонениями средних траекторий из-за ошибок в
подготовке стрельбы (рис. 39). Поэтому при определении дейст-
вительности стрельбы с учетом ошибок в стрельбе необходимо
брать размеры суммарных (приведенных) срединных отклонений, совмещая центр суммарного рассеивания с серединой цели.

Вероятность попадания и ее зависимость
от различных причин
Вследствие рассеивания пуль (гранат) и ошибок в подготовке
стрельбы при выстреле можно попасть в цель или сделать промах.
Возможность попасть в цель характеризуется вероятностью попа-
дания.
Вероятностью попадания называется число, характеризующее
степень возможности попадания в цель при данных условиях
стрельбы.
Вероятность попадания изменяется от нуля до единицы, так
как попадания могут появиться при всех выстрелах, или только
при части их, или совсем не появиться. Вероятность попадания
выражается обычно десятичной дробью или в процентах.
Для определения вероятности попадания необходимо в каж-
дом отдельном случае найти ту часть площади рассеивания, кото-
рой будет накрыта цель, и на основании закона рассеивания под-
считать процент попаданий, приходящийся на площадь цели.
Вероятность попадания может быть определена на основании
результатов опытных стрельб.
Отношение числа попаданий к числу всех произведенных вы-
стрелов называется частотой попадания.
При достаточно большом числе стрельб, произведенных в воз-
можно одинаковых условиях, частота попадания изменяется в
очень узких пределах, колеблясь около среднего значения. Сред-
нее значение частоты попадания, найденное в результате этих
стрельб, и будет вероятностью попадания для данных условий.
Вероятность попадания будет тем больше, чем больше размеры
пели.
Величина вероятности попадания зависит:
от положения средней точки попадания относительно центра
цели (рис. 40); чем ближе средняя точка попадания к центру цели,
гем более кучной частью площади рассеивания будет накрываться
цель, тем больше будет вероятность попадания;
от размеров цели (рис. 41); при совпадении средней точки по-
падания с центром цели и при одних и тех же размерах площади
рассеивания вероятность попадания будет тем больше, чем боль-
ше размеры цели;
от размеров площади рассеивания (рис. 42); при одних и тех же
размерах цели вероятность попадания будет тем больше, чем ме-
ньше будет площадь рассеивания; если рассеивание не выходит
из пределов цели, то вероятность попадания будет равна 100 %;
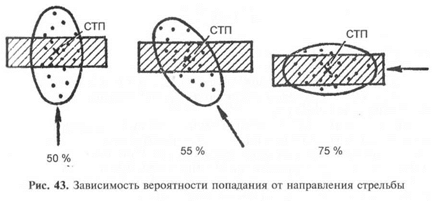
от направления стрельбы (рис. 43); если цель имеет большое
протяжение по фронту и малое в глубину, то наибольшая вероят-
ность попадания будет при стрельбе во фланг цели; если цель глу-
бокая, то наибольшая вероятность попадания будет при фрон-
тальном обстреле цели.

Для увеличения вероятности попадания необходимо:
тщательно производить выверку прицельных приспособлений
и приводить оружие к нормальному бою;
умело выбирать прицел и точку прицеливания, обеспечива-
ющие совмещение средней точки попадания с серединой
цели;
использовать для стрельбы моменты, когда цель наиболее уяз-
вима (поднялась во весь рост, подставила свой фланг или борт
и др.);
принимать меры к уменьшению действия причин, приводящих
к рассеиванию пуль (гранат), и возможно точнее наводить оружие
в цель.
Способы определения вероятности попадания
Вероятность попадания в цель может быть определена сравне-
нием площади цели с площадью сердцевины рассеивания, по
шкале рассеивания, по таблице значений вероятностей и по сетке
рассеивания.
При стрельбе автоматическим огнем (очередями) для вычисле-
ния вероятности попадания берутся характеристики суммарного
рассеивания.
Если цель по своим размерам равна сердцевине рассеивания
или меньше ее, то вероятность попадания в цель определяется
приближенно сравнением площади цели с площадью сердцевины
рассеивания. При этом допускается, что рассеивание пуль в пре-
делах сердцевины равномерное.
Вероятность попадания в цель будет во столько раз меньше ве-
роятности попадания в сердцевину, во сколько раз площадь цели
меньше площади сердцевины, т. е.

Если в каком-либо направлении цель по своим размерам боль-
ше сердцевины рассеивания, то вероятность попадания в нее мо-
жет быть определена по шкале рассеивания. При этом вероятность
попадания в цель определяется как произведение вероятности по-
падания в полосу, равную высоте (глубине) цели, на вероятность
попадания в полосу, равную ширине цели, т. е.
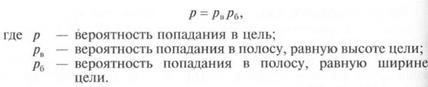
Для определения вероятности попадания в полосу, равную вы-
соте (ширине) цели, необходимо: вычертить в произвольном мас-
штабе цель и на ней в том же масштабе шкалу рассеивания, на-
пример по высоте; подсчитать по шкале рассеивания процент
попаданий, приходящийся в полосу, равную высоте цели; вычер-
тить на цели шкалу рассеивания по боковому направлению и так-
же подсчитать по ней процент попаданий в полосу, равную шири-
не цели.
При расчетах по шкале рассеивания с масштабом в одно сре-
динное отклонение допускают, что рассеивание равномерно в
пределах полосы, равной по ширине одному срединному откло-
нению.
Если цель не является прямоугольником, а имеет фигурное
очертание, то сначала по шкале рассеивания определяется веро-
ятность попадания в прямоугольник, описанный вокруг фигур-
ной цели. Затем полученную вероятность умножают на коэффи-
циент фигурности, равный отношению площади цели к площади
описанного вокруг цели прямоугольника, т. е.
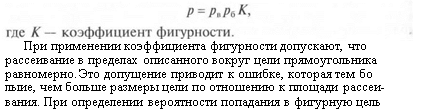
коэффициент фигурности можно применять только в тех случаях,
когда размеры цели меньше размеров полного рассеивания.
Для более точных расчетов коэффициент фигурности опреде-
ляется как отношение вероятности попадания в цель к вероятно-
сти попадания в прямоугольник, описанный вокруг цели.
Для удобства определения вероятности попадания иногда фи-
гурную цель заменяют равновеликим прямоугольником, стороны
которого соответственно равны произведению ширины (высоты)
мишени на корень квадратный из коэффициента фигурности
(рис. 44).
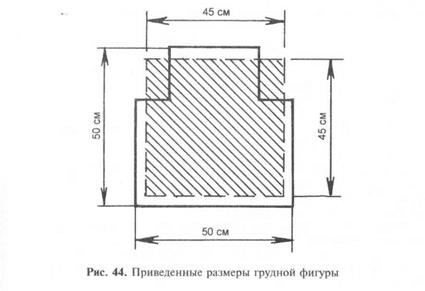
Найденную вероятность попадания в такой прямоугольник
принимают за вероятность попадания в фигурную цель.
Для более точного определения вероятности попадания в цель
пользуются таблицей значений вероятностей (шкалой рассеива-
ния), рассчитанной с учетом неравномерности рассеивания через
каждую. десятую или сотую и так далее долю срединного отклоне-
ния. При этом допускают, что рассеивание равномерно только в
пределах полосы по ширине, равной десятой, сотой и так далее
поле срединного отклонения.
Для определения вероятности попадания по таблице значений
вероятностей необходимо:
подсчитать отношения половины высоты (глубины) или ши-
рины цели к срединному отклонению по высоте (дальности) или
боковому направлению; эти отношения в таблице обозначены че-
рез В;
в графе В найти цифры, соответствующие этим отношениям;
стоящие рядом в графе Ф (В) цифры являются вероятностью по-
падания в полосы, равные высоте (глубине) или ширине цели.
Вероятность попадания в цель прямоугольной формы будет
равна произведению вероятности попадания в полосу, равную
высоте (глубине) цели, на вероятность попадания в полосу, рав-
ную ширине цели.
Если цель по своей форме отличается от прямоугольника, то
найденную вероятность попадания необходимо умножить на ко-
эффициент фигурности. Вероятность попадания в такую цель
можно найти также по приведенным размерам цели без использо-
вания коэффициента фигурности, воспользовавшись формулой

Для определения вероятности попадания по таблице вероятно-
стей в круглую мишень при площади рассеивания, близкой по
форме к кругу, и при совмещении средней точки попадания с
центром мишени необходимо:
определить отношение радиуса круглой мишени к радиусу
круга рассеивания, вмещающего 50 % попаданий;
по таблице в графе В найти это отношение; стоящая рядом в
графе Ф (В) цифра будет являться вероятностью попадания в
цель.
Когда средняя точка попадания не совпадает с серединой цели
(рис. 45), для определения вероятности попадания в цель необхо-
димо:
1. Определить вероятность попадания в полосу, равную высоте
(глубине) цели, для чего:
определить вероятность попадания в полосу, высота (глубина)
которой равна расстоянию от оси рассеивания по высоте (дально-
сти) до верхнего (дальнего) края цели; для этого найти отношение
высоты (глубины) этой полосы к срединному отклонению по вы-
соте (дальности), т. е. В, и по таблице вероятностей взять полови-
ну (1/2) значения, указанного в графе Ф (В);
определить таким же образом вероятность попадания в полосу,
высота (глубина) которой равна расстоянию от этой же оси рассе-
ивания до нижнего (ближнего) края цели;
определить вероятность попадания в полосу, равную высоте
(глубине) цели; она будет равна: если средняя точка попадания
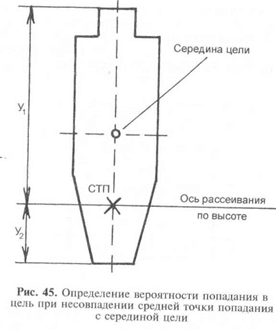
расположена в пределах цели, — сумме вероятностей попадания в
эти полосы; если средняя точка попадания вне пределов цели, —
разности вероятностей попадания в эти полосы.
2. Подобным образом определить вероятность попадания в по-
ичу, равную ширине цели.
3. Определить вероятность попадания в цель, для чего вероят-
на ть попадания в полосу, равную высоте цели, умножить на ве-
роятность попадания в полосу, равную ширине цели. Если цель
имеет фигурное очертание, то полученную вероятность умножить
на коэффициент фигурности или для определения вероятности
попадания взять приведенные размеры цели, воспользовавшись
формулой


Знак «плюс» (+) берется, когда ось рассеивания проходит че-
рез цель, а знак «минус» (-) — когда ось рассеивания вне цели.
Вероятность попадания в цель любого очертания и при любом
расположении средней траектории может быть определена гра-
фическим способом по сетке рассеивания (рис. 46).

Сетка рассеивания составляется проведением прямых линий,
параллельных осям рассеивания, через целые срединные откло-
нения или доли их. В результате этого вся площадь рассеивания
разбивается на ряд прямоугольников. Вероятности попадания в
образовавшиеся прямоугольники подсчитываются умножением
вероятностей попадания в полосы, которыми образуются эти
прямоугольники.
Определение вероятности попадания по сетке рассеивания
производится в той же последовательности, что и по шкале рассе-
ивания. Для этого надо начертить в условном масштабе цель и па
нее наложить в том же масштабе сетку рассеивания так, чтобы
центр рассеивания был в точке согласно условиям стрельбы. 3|
тем подсчитать вероятность попадания в цель суммированием ве-
роятностей попадания в прямоугольники, накрывающие цель;
причем там, где прямоугольники не полностью входят в цель, не
роятности берутся примерным сравнением площади, занятой цс
лью, с площадью всего прямоугольника:
Для определения вероятности попадания в одиночную (групповую прерывчатую) цель при стрельбе с искусственным рассеивани-
ем по фронту необходимо найти вероятность попадания в полосу,
равную высоте цели, и умножить ее на отношение площади оди-
ночной цели (занятой всеми фигурами) к площади прямоугольни-
ка ширина которого равна ширине фронта искусственного рассе-
ивания, а высота — высоте цели. При этом допускается, что
рассеивание пуль по боковому направлению равномерно и вероят-
ность попадания в полосу, равную фронту цели (рассеивания),
равна 100 %. Если групповая цель состоит из одинаковых по разме-
рам фигур, то ее площадь определяется умножением площади од-
ной фигуры на число фигур. Тогда получим:
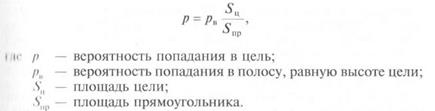
Вероятность попадания в цель с учетом ошибок в подготовке
стрельбы определяется вышеуказанными способами. При этом
кроме характеристик рассеивания учитываются ошибки в подго-
товке стрельбы и принимается, что средняя точка попадания про-
ходит через середину цели.
Вероятность попадания при стрельбе из автомата, а также из
ручного пулемета из положения с колена, стоя, на ходу с корот-
кой остановки определяется вышеуказанными способами отдель-
но для первых пуль очередей и для последующих пуль очередей.
Вероятности попадания для первой пули очереди и для после-
дующей пули очереди и коэффициент зависимости между ними
учитываются при определении вероятности поражения цели заданным количеством патронов.
При определении вероятности попаданий используются таблицы значений вероятности попадания и поражения цели, размеры целей и срединные ошибки подготовки исходных данных, приведенные в наставлениях по стрелковому делу (приложение 4 к Основам стрельбы из стрелкового оружия).
Вероятность поражения цели
При стрельбе из стрелкового оружия по одиночным живым це-
лям и из гранатометов по одиночным бронированным целям одно попадание обычно дает поражение цели. Поэтому под вероятно-
стью поражения одиночной цели понимается вероятность полу-
чения хотя бы одного попадания при заданном числе выстрелов.
Вероятность поражения цели при одном выстреле (Р,) числен-
но равняется вероятности попадания в цель (р). Расчет вероятно-
сти поражения цели при этом условии сводится к определению
вероятности попадания в цель.
Вероятность поражения цели (Р,) несколькими одиночными
выстрелами, одной очередью или несколькими очередями, когда
вероятность попадания для всех выстрелов одинакова, равна еди-
нице минус вероятность промаха в степени, равной количеству
выстрелов (я), т. е.
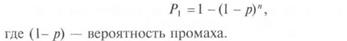
Найденная таким образом вероятность поражения цели харак-
теризует надежность стрельбы, т. е. показывает, в скольких случа-
ях из ста в среднем цель в данных условиях будет поражена не ме-
нее чем при одном попадании.
Стрельба считается достаточно надежной, если вероятность
поражения цели не менее 80 %.

Вероятность поражения цели несколькими выстрелами одной
очередью или несколькими очередями, когда вероятность попа-
дания первых и последующих пуль (очередей) изменяется от вы-
стрела (очереди) к выстрелу (очереди), равна единице минус ве-
роятность промахов первых и последующих пуль очереди (очередей):
При определении вероятности поражения целей автоматиче-
ким огнем по формулам, указанным выше, получаются завышен-
ные результаты (на 3—7 %). Поэтому при более точных подсчетах
вероятностей поражения цели пользуются специальными форму-
лами, учитывающими коэффициент зависимости выстрелов.
Математическое ожидание числа (процента)
пораженных фигур групповой цели
Математическим ожиданием числа (процента) пораженных фи-
гур в групповой цели называется среднее число (процент) пора-
женных фигур, которое можно получить, если повторить стрельбу
большое число раз в одинаковых условиях.
Среднее число пораженных фигур в групповой цели численно
равно сумме вероятностей поражения всех одиночных фигур.
Если групповая цель состоит из одинаковых по размерам фигур,
то среднее число пораженных фигур в групповой цели (Аn) чис-
ленно равно вероятности поражения одной фигуры (Р1), умно-
женной на число фигур в ней (N), т. е.
AN =P 1N.
Если неизвестно количество фигур, составляющих групповую
цель, то математическое ожидание числа пораженных фигур ха-
рактеризуется средним ожидаемым процентом пораженных фи-
гур в ней.
Средний ожидаемый процент пораженных фигур в групповой
цели, состоящей из одинаковых по размерам фигур, при стрельбе
с искусственным рассеиванием или последовательным переносом
огня численно равен вероятности поражения любой одиночной
фигуры групповой цели при том же числе выстрелов, т. е.
Ап ~ P1 (в процентах).
Математическое ожидание числа попаданий
и средний ожидаемый расход боеприпасов и времени
Математическим ожиданием числа попаданий называется сред-
нее число попаданий, которое можно получить, если повторить
стрельбу большое число раз в возможно одинаковых условиях.
Математическое ожидание числа попаданий при одном вы-
стреле численно равно вероятности попадания.
Математическое ожидание числа попаданий при нескольких
выстрелах (а„), если вероятность попадания (р) для всех выстре-
лов одинакова, равно произведению количества выстрелов (и) на
вероятность попадания при одном выстреле, т. е.
ап = пр.


ля стрельбы по живым целям требу






