На рис. 3 а в виде диаграммы показано распределение результатов n измерений некоторой физической величины x относительно среднего значения 
. Ось абцисс разбита на равные интервалы шириной d x. Высота каждого столбика диаграммы показывает количество N (x) близких результатов измерений, попадающих в интервал d x с центром в точке x. Пунктирная кривая (которая здесь не является симметричной) вычерчена, чтобы показать зависимость числа отсчетов N (x) от x при относительно небольшом числе измерений.
Рис. 3.
Если число измерений n становится очень большим, то результаты измерений стремятся к симметричному распределению около среднего значения (рис. 3 б). Как показывается в теории вероятности, в идеальном случае такая кривая описывается аналитическим выражением
, (4)
где n - очень большое число измерений, - среднее значение, а s - стандартное отклонение, определяемое по формуле (2) при условии n ® ¥. Величина s2 называется дисперсией. Уравнение (4) представляет собой распределение Гаусса или нормальное распределение.
Для большого числа измерений n распределение Гаусса описывает теоретическое распределение измеренных значений x относительно среднего значения . Если измерения выполняются с высокой точностью, то s будет малым, и нормальное, или Гауссово, распределение будет иметь острый пик при x = (рис. 4).
Рис. 4.
Разделив обе части уравнения (4) на n и определив N (x)/ n как Р (x), имеем:
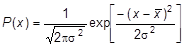. (5)
Выражение (5) имеет смысл плотности вероятности того, что в результате измерения мы получим значение х. Таким образом, вероятность того, что измеренное значение x будет лежать в некотором интервале x 1 < x < x 2, определяется площадью под соответствующим участком кривой:
.
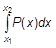Заметим, что наиболее вероятным значением, которое можно ожидать в результате измерения, является среднее значение. Следует также отметить, что полная площадь под кривой, представляющей функцию P (x), всегда равна единице:
.
Особенностью распределения Гаусса является то, что 68% всех результатов измерений попадают в интервал от 
до 
, 95% всех результатов измерений попадают в интервал от 
до 
, а 99,7% всех результатов измерений попадают в интервал от 
до 
. Другими словами, с вероятностью 0,68 истинное значение величины x лежит в интервале 
, с вероятностью 0,95 – в интервале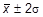 
, и т.д.
Следует иметь в виду, что распределение Гаусса не является единственно возможным. Могут существовать и другие виды распределений, например, распределение Пуассона, экспоненциальное распределение, c2-распределение и т.д. Тем не менее, нормальное распределение встречается достаточно часто, причём все остальные распределения в пределе (при n ® ¥) переходят в распределение Гаусса.
На практике, однако, число измерений обычно сравнительно невелико. В этом случае для повышения достоверности результатов измерений следует при оценке погрешности пользоваться модифицированными формулами. Так, абсолютная погрешность D x измеряемой величины x при относительно малом (скажем, менее 10) количестве измерений определяется как:
, (6)
где t a, n – коэффициент Стьюдента, зависящий от числа измерений n и от величины доверительной вероятности a. Значения коэффициентов t a, n для некоторых различных значений n и a приведены в табл. 1.
В соответствии с действующими государственными стандартами рекомендуется при оценке погрешностей пользоваться доверительной вероятностью a = 0,95.
Таблица 1.
 n
| a | 0,90 | 0,95 | 0,98 |
| 6,31 | 12,71 | 31,82 | ||
| 2,92 | 4,30 | 6,96 | ||
| 2,35 | 3,18 | 4,54 | ||
| 2,13 | 2,78 | 3,75 | ||
| 2,02 | 2,57 | 3,36 | ||
| 1,94 | 2,45 | 3,14 | ||
| 1,90 | 2,36 | 3,00 | ||
| 1,86 | 2,31 | 2,90 | ||
| 1,83 | 2,26 | 2,82 |
Таким образом, окончательный результат измерений запишется в виде:
, (a), (7)
где D x определяется из выражения (6). Запись (7) означает, что истинное значение величины x с вероятностью a находится в интервале значений от 
до 
.
