Пример 1. Система содержит n=3 одинаковых элемента – один основной и два резервных (кратность резервирования 2). Интенсивность отказов каждого элемента λ= 0,05 1/час. Постоянное резервирование без перераспределения нагрузки или замещением с нагруженным резервом.
Найти вероятность безотказной работы системы и интенсивность отказов при t= 10,20, 50, 100 час, а также среднее время безотказной работы.
Используемые формулы
| t,час | R рез | λ, /1час | R̃ рез | λ̃, /1час |
| 0,939 | 0,015 | 0.986 | 0,00385 | |
| 0,747 | 0.0296 | 0,92 | 0,01 | |
| 0.227 | 0,0458 | 0,544 | 0,0236 | |
| 0,02 | 0,0497 | 0,125 | 0.0338 |
Для одного элемента
T 0 = 20 час
T рез = 20(1+1/2+1/3)= 36,7 час █
Пример 2. Теже данные, только резерв активный ненагруженный. Найти те же показатели
Используемые формулы
R̃ рез (t) = 
λ̃ рез (t) =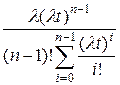 
.
См. таблицу.
T̃ рез = nT0 = 3∙20= 60 час █
Пример 3. Определить кратность m постоянного резервирования, обеспечивающую вероятность безотказной работы элемента 0,96 в течение t =150 час. Среднее время безотказной работы элемента T 0 =300 час. Рассмотреть два варианта: а) экспоненциальный закон и б) закон Рэлея для времени безотказной работы.
Независимо от закона распределения
,
где 
– вероятность безотказной работы системы с резервом, R (t) – вероятность безотказной работы элемента, а n – общее число элементов в системе (n= m +1). Отсюда
Для варианта а)
, где λ =1/ T 0 .
, и
=2,45.
Следует взять m = 3.
Для варианта б)
, 
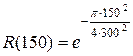= 0,822, и
= 0,87.
Достаточно взять m = 1.
Отметим влияние закона распределения времени безотказной работы.▲
Пример 4. Система электроснабжения состоит из n =4 генераторов мощностью 18 кВт каждый. Необходимо не менее 30 кВт. Интенсивность отказов каждого генератора λ= 0,15∙10-3 1/час. Найти вероятность безотказной работы за время t =600 час и среднее время безотказной работы.
Обозначим через p вероятность безотказной работы одного генератора за время t. В случае экспоненциального закона
p = e-λt .
Для безотказной работы системы необходимо не менее двух работоспособных генераторов (или допустим отказ не более 2-х).
.
Находим для t = 600 час
= 0,9139
и далее
Среднее время безотказной работы найдем по формуле (для случая экспоненциального распределения c интенсивностью отказов λ)
,
где k – минимально допустимое число работоспособных элементов. После подстановок получим
T рез = 103/0,15∙(1/2+1/3+1/4)= 7220 час.
Без резерва λ = 0,3∙10-3; R (600) = e -0,18 = 0,835; T = 3333 час. ▲
Пример 5. Интенсивность отказов блока λ 1= 10-4 1/час. Что лучше: применить ненагруженный резерв в виде такого же блока или другой блок с интенсивностью отказов λ 2= 10-5 1/час (стоимость одинакова). Сравнение провести по вероятности безотказной работы в течение 103, 5∙103, 104 час.
| t, час | 
| 
|
| 103 | e -0,1(1+0,1)=0,9953 | e -0,01 =0,990 |
| 5∙103 | e -0,5(1+0,5)=0,9075 | e -0,05 =0,9512 |
| 104 | e -1(1+1)= 0,7358 | e -0,1 = 0,9048 |
Для t = 5∙103 и 104 час лучше другой блок. ▲
Пример 6. Система питания состоит из выпрямителя, работающего от сети (λ 1= 0,3∙10-3 1/час) и резервного аккумулятора (λ 2= 5∙10-3 1/час). Резерв считать ненагруженным. Найти вероятность безотказной работы в течение t = 100 час. Сравнить с вероятностью безотказной работы нерезервированной системы.
=
= 
=
= 
.
Для нерезервированной системы
R (t) = e- 0,03 = 0,9704. ▲
