Ф.И.О. Сидоров Иван Петрович.
Посылка содержит 12 различных букв и интервал между словами.
1.5.1. Число разрядов кода:
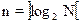 (1.10)
(1.10)
где, N=13 - различных символов.
n=4
1.5.2. Составление кодовой таблицы преобразователя кода.
В кодовую таблицу добавим синхроимпульсы между посылками в виде трёх пробелов. Объясняется это тем, что между словами возможна кодовая комбинация 1000 0000 0001 две буквы и пробел (Н  С), что можно спутать с двумя символами
С), что можно спутать с двумя символами 
 . Синхронизирующая пауза должна быть не менее 0000 0000 000, кроме того, первую букву можно передать как 0001 так и 1000, в первом случае усложняется схема синхронизации приёмника по тактам, а во втором - по фазе. Решением проблемы может быть применение старт - стопного механизма. Для циклической системы передачи с небольшим количеством информационных импульсов достаточно одного стартового, в нашем примере 21 символ передаются 84 импульсами и для синхронизации начала посылки нужно взять не менее двух единичных импульсов. Синхронизирующая пауза примет вид: 0000 0000 0000 0101 - наименьшая оптимальная длина для этого примера.
. Синхронизирующая пауза должна быть не менее 0000 0000 000, кроме того, первую букву можно передать как 0001 так и 1000, в первом случае усложняется схема синхронизации приёмника по тактам, а во втором - по фазе. Решением проблемы может быть применение старт - стопного механизма. Для циклической системы передачи с небольшим количеством информационных импульсов достаточно одного стартового, в нашем примере 21 символ передаются 84 импульсами и для синхронизации начала посылки нужно взять не менее двух единичных импульсов. Синхронизирующая пауза примет вид: 0000 0000 0000 0101 - наименьшая оптимальная длина для этого примера.
Завершать посылку можно контрольной суммой (ограниченное подсчитанное число единичных или нулевых импульсов), но в нашем примере код неизменный и циклически повторяется, при сбое приёмника всегда есть возможность его восстановить, да и всю посылку в общем случае можно считать синхронизирующим кодом, преамбулой перед более сложной передачей данных. Синхронизирующие импульсы можно сразу вставить в кодовую таблицу, но лучше после добавить их на заранее предусмотренное место. Комбинация номер 0 (табл. 2.1) как раз и является таким местом, кроме этого выходной код буквы номер 0 автоматически получается после асинхронного сброса всей схемы.
Таблица 2.1.
Кодирование символов посылки
| Входное слово преобразователя кода | Выходное слово | ||||||||||
| № такта | Символ | Х5 | Х4 | Х3 | Х2 | Х1 | № кода буквы | Y4 (8) | Y3 (4) | Y2 (2) | Y1 (1) |

| |||||||||||
| С | |||||||||||
| И | |||||||||||
| Д | |||||||||||
| О | |||||||||||
| Р | |||||||||||
| О | |||||||||||
| В | |||||||||||

| |||||||||||
| И | |||||||||||
| В | |||||||||||
| А | |||||||||||
| Н | |||||||||||

| |||||||||||
| П | |||||||||||
| Е | |||||||||||
| Т | |||||||||||
| Р | |||||||||||
| О | |||||||||||
| В | |||||||||||
| И | |||||||||||
| Ч | |||||||||||

| 0(~) | 0(~) | 0(~) | 0(~) | |||||||

| 0(~) | 0(~) | 0(~) | 0(~) | |||||||

| 0(~) | 0(~) | 0(~) | 0(~) | |||||||
| Сброс | 0(~) | 0(~) | 0(~) | 0(~) | |||||||

| |||||||||||
| С | |||||||||||
| Циклически повторяется | |||||||||||
| - | ~ | ~ | ~ | ~ | ~ | ||||||
| - | ~ | ~ | ~ | ~ | ~ | ||||||
| До 11111 безразлично |
Таблица имеет продолжение до 31 комбинации, но с такта номер 25 включительно и до конца кодовая комбинация выходного слова безразлична, потому что этих комбинаций никогда не будет за счёт асинхронного сброса в нуль входного слова.
1.5.3. Выходные функции Yn.
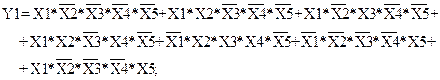 (1.11)
(1.11)
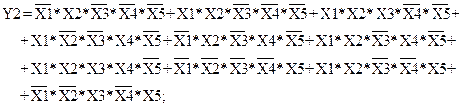 (1.12)
(1.12)
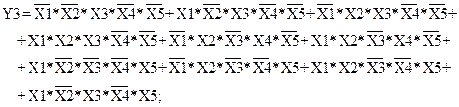 (1.13)
(1.13)
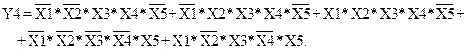 (1.14)
(1.14)
1.5.4. Минимизация функций преобразователя кода.
Минимизировать можно любым известным методом, например методом Карно – Вейча.
Строим карту Карно для входного слова. Шаблон карты Карно для входного слова, состоящего из пяти букв, показан на рис. 1.7. Каждой стороне диаграммы соответствует своя переменная Хр (р=1, 2, 3, 4, 5), причем одной половине стороны соответствует первичный терм Xp, а другой - первичный терм 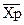 . Поэтому каждой клетке будет соответствовать совокупность первичных термов (Хр)е, (
. Поэтому каждой клетке будет соответствовать совокупность первичных термов (Хр)е, (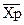 )е, а номер данной клетки будет определяться числом i=e5,e4,e3,e2,е1. Любой минтерм представляет собой функцию, равную «1» только в одной точке, области определения, поэтому на диаграмме он представляется единицей, стоящей только в одной клетке с номером i.
)е, а номер данной клетки будет определяться числом i=e5,e4,e3,e2,е1. Любой минтерм представляет собой функцию, равную «1» только в одной точке, области определения, поэтому на диаграмме он представляется единицей, стоящей только в одной клетке с номером i.
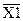
| Х1 | 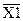
| Х1 | 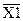
| |||||
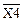
| 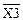
| ||||||||
| Х3 | |||||||||
| Х4 | |||||||||
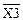
| |||||||||
| Х2 | 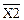
| Х2 | 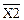
| ||||||
| Х5 | 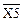
|
Рис. 1.7.
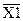
| Х1 | 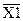
| Х1 | 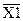
| |||||
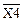
|  0 0
|  1 1
| 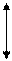  1 1
|  1 1
| 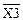
| ||||
| ~ | ~ | Х3 | |||||||
| Х4 |   ~ ~
| ~ | ~ | ~ |  1 1
| ||||
| ~ | ~ |  ~ ~
| ~ |  1 1
| 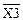
| ||||
| Х2 | 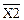
| Х2 | 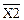
| ||||||
| Х5 | 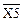
|
а)
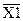
| Х1 | 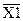
| Х1 | 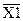
| |||||
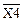
|  1 1
|  1 1
|   1 1
|  1 1
| 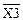
| ||||
| ~ | ~ | Х3 | |||||||
| Х4 | ~ |  ~ ~
| ~ | ~ | |||||
| ~ |  ~ ~
|  ~ ~
| ~ |  1 1
|  1 1
| 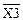
| |||
| Х2 | 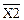
| Х2 | 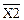
| ||||||
| Х5 | 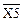
|
б)
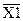
| Х1 | 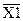
| Х1 | 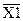
| |||||
 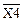
|  1 1
|  0 0
| 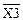
| ||||||
| ~ | ~ | Х3 | |||||||
| Х4 | ~ | ~ | ~ | ~ | |||||
 ~ ~
|  ~ ~
| ~ | ~ |  1 1
| 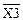
| ||||
| Х2 | 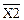
| Х2 | 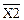
| ||||||
| Х5 | 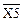
|
в)
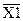
| Х1 | 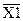
| Х1 | 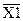
| |||||
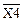
|  1 1
| 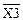
| |||||||
 ~ ~
|  ~ ~
|  0 0
|  0 0
|  0 0
| Х3 | ||||
 Х4 Х4
| ~ | ~ | ~ |  ~ ~
| |||||
 ~ ~
| ~ |  ~ ~
|  ~ ~
|  0 0
| 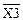
| ||||
| Х2 | 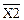
| Х2 | 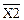
| ||||||
| Х5 | 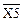
|
г)
Рис. 1.8. Диаграммы выходных функций Y
преобразователя кода: а - Y1; б - Y2; в – Y3; г – Y4.
Примечание: Схемным способом можно обеспечить безразличие("~") 22, 23 и 24 комбинациям, путём отключения преобразователя кода от канала связи на время выполнения этих комбинаций.
Методом склеивания объединяем рядом стоящие единичные минтермы. Рядом стоящие считаем те минтермы, у которых разные только одна буква по инверсии, что позволяет (в алгебраическом виде) её заключить в скобки и сократить, получив импликант. Если находим второй импликант, отличающийся также на одну букву по инверсии то, между ними также проводим операцию склеивания и так до тех пор, пока не получим простой импликант. Следовательно, рядом стоящих единиц может быть ряд 2n где, n=1,2,3…. Клетки содержащие знак "~" необходимо доопределить, т. е. поставить "1" или "0", выбираем те значения, которые дают наименьшее количество букв в минимизированной функции. Из всех возможных импликантов необходимо выбрать оптимальные с учётом других функций автомата с целью использования одних и тех промежуточных частей схемы для различных букв выходного слова преобразователя. Не склеенные клетки дописываем в выходную функцию.
Запишем выходные функции в минимальной дизъюнктивной нормальной форме (МДНФ):
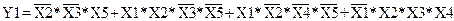 ; (1.15)
; (1.15)
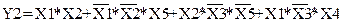 ; (1.16)
; (1.16)
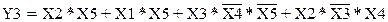 ; (1.17)
; (1.17)
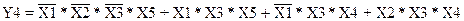 . (1.18)
. (1.18)






