Техника многофакторного регрессионного анализа в MS Excel практически не отличается от техники двухфакторного – используется тот же самый инструмент – Регрессия из пакета анализа. При этом предполагается, что в исходной таблице, описывающей случайные данные, каждый следующий столбец содержит выборку значений следующей по порядку случайной переменной; в соответствующем окошке указывается сплошная область значений влияющих переменных (факторов) многофакторной линейной модели.
Что касается сути самого анализа, в многофакторной регрессионной модели дополнительно учитываются и анализируются следующие характерные аспекты:
Ø коэффициент многофакторной детерминации (определение аналогично двухфакторной модели); с учетом сокращения степеней свободы, вызванным многофакторностью, применяется скорректированный коэффициент многофакторной детерминации 
, где 
- количество оцениваемых параметров;
Ø тест общей значимости качества регрессии; производится на основе статистики Фишера ( 
- распределение), для чего вычисляется значение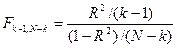 
, которое сравнивается с соответствующим критическим значением. Если вычисленное значение превосходит критическое при наперед заданном уровне значимости, то принимается гипотеза, что параметры регрессии не равны 0 и 
существенно отличается от 0.
Ø парциальные (частные) коэффициенты корреляции между факторами; парциальные коэффициенты корреляции вычисляются между каждым их влияющих факторов и зависимой переменной, очищенные от влияния остальных факторов. Так, например, для 3-факторной линейной регрессионной модели 
и 
, причем коэффициенты принимаются со знаками соответствующих параметров регрессии.
Специальным приемом в многофакторном регрессионном анализе явлений и процессов с наличием в них резких изменений (шоков) является использование грубых (шоковых) переменных. Присутствие шоков в модельных данных часто можно определить визуально (например, по виду диаграммы рассеяния). Шоковые переменные обычно задаются как бинарные, т.е. могут принимать только два различных значения – чаще всего 0 и 1. С их помощью моделируются резкие изменения в модели, вызванные психологическими, социальными, экономическими и т.п. стрессами. Дополнительная шоковая переменная D = (0,1) используется в технике регрессионного анализа наравне с другими переменными.
С использованием техники многофакторного регрессионного анализа проводится также статистический анализ распределенных лаговых моделей. Лаговые (с задержками) модели часто возникают в практике анализа случайных временных рядов; в моделях такого сорта предполагается, что на зависимую переменную оказывают влияние значения некоторой однородной объясняющей переменной, но в различные моменты (периоды) времени T. Общая форма такой модели выглядит следующим образом:
Приведение к стандартному виду такой «многофакторной» модели очевидно – «смещенные во времени» переменные рассматриваются как «независимые». Принципиальное отличие лаговой модели от «чистой» многофакторной – наличие сильных корреляций между «соседними» факторами.
Самостоятельно: объяснить каково должно быть соотношение между 
, 
и 
с тем, чтобы 3-факторная модель указывала на реальное и независимое влияние объясняющих переменных на зависимую. Задача 1: провести 3-факторный регрессионный анализ с шоковой переменной. Задача 2: провести анализ 2-лаговой модели.
