При переводе чисел из десятичной системы счисления в любую другую необходимо перевести целую и дробную части отдельно, а затем объединить результаты в новое число.
Целая часть переводится путем деления на основание системы счисления до тех пор, пока частное от деления и остатки не станут меньше основания новой системы счисления. Результатом перевода будут являться все остатки и частное, записанные справа налево.
Пример: перевести число 575 в двоичную, восьмеричную и шестнадцатеричную системы счисления.
Решение:
►Переведем число в двоичную систему счисления:
| ||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||
Примечание: при делении 575 на 2 (основание системы счисления) получаем частное 287 и остаток 1. Полученное частное снова делим на 2, поскольку оно больше основания системы счисления. При делении 287 на 2 получаем частное 143 и остаток 1. Поскольку частное вновь оказалось больше основания двоичной системы счисления, то продолжаем процесс деления. Завершаем процедуру деления, когда полученное частное и остаток оказываются меньше основания двоичной системы счисления.
Для окончательной записи результата перевода числа в новую систему счисления все полученные остатки и последнее частное записываем справа налево:
.
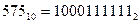Аналогично переводится число в восьмеричную и шестнадцатеричную системы счисления.
Перевод в восьмеричную систему счисления:
| ||||||||||
| ||||||||||
.
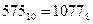Перевод в шестнадцатеричную систему счисления:
| ||||||
| ||||||
.
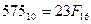Примечание: числу 15 в шестнадцатеричной системе счисления соответствует латинская буква F.◄
Дробная часть переводится путем умножения дробной части исходного числа на основание системы счисления. При этом целая часть полученного произведения заносится в дробный разряд искомого числа, а дробная часть вновь умножается на основание системы счисления.
Пример: перевести число 0,173 в двоичную, восьмеричную и шестнадцатеричную системы счисления.
Решение:
►Перевод в двоичную систему счисления:
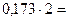
| 0, | |
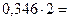
| 0, | |
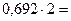
| 1, | |
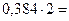
| 0, | |
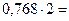
| 1, | |
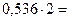
| 1, | |
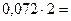
| 0, | |
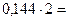
| 0, |
Результат:
.
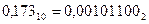Примечание: при переводе дробной части может получаться периодичная дробь. Если такая дробь не появилась, то будем ограничиваться восемью знаками после запятой.
Перевод в восьмеричную систему счисления:
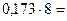
| 1, | |
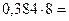
| 3, | |
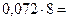
| 0, | |
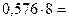
| 4, | |
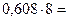
| 4, | |
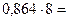
| 6, | |
| 7, | |
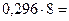
| 2, |
Результат:
.
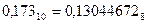Перевод в шестнадцатеричную систему счисления:
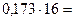
| 2, | |
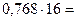
| 12, | |
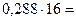
| 4, | |
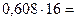
| 9, | |
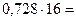
| 11, | |
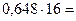
| 10, | |
| 5, | |
| 14, |
Результат:
.◄
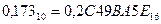Обратный перевод чисел из любой системы счисления в десятичную осуществляется по формуле расширенной записи числа. По этой же формуле осуществляется проверка правильности перевода из десятичной системы в любую другую.
Пример: выполнить проверку перевода числа 575 в двоичную систему счисления, а числа 0,173 – в восьмеричную.
Решение:
► 
◄
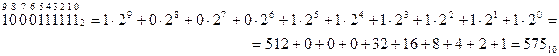
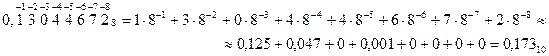3 АРИФМЕТИЧЕСКИЕ ОПЕРАЦИИ В ДВОИЧНОЙ СИСТЕМЕ СЧИСЛЕНИЯ
Рассмотрим более подробно арифметические операции в двоичной системе счисления. Арифметика двоичной системы счисления основывается на использовании таблиц сложения, вычитания и умножения цифр. Рассмотрим подробно каждую операцию.
| + | - | * | ||||||||
Таблица двоичного сложения предельно проста. Только в одном случае, когда производится сложение 1+1, происходит перенос в старший разряд.
Пример: рассмотрим несколько примеров сложения двоичных чисел:
| 1 1 0 1 | 1 1 1 1 1 | 1 0 1 0 0 1 1, 1 1 1 | |||||||||||
| 1 0 1 0 | 1 0 1 1 | 1 1 0 0 1, 1 1 0 | ||||||||||||
| 1 0 0 1 1 | 1 1 0 0 0 | 1 0 0 0 0 0 | 1 1 0 1 1 0 1, 1 0 1 |
При выполнении операции вычитания всегда из большего по абсолютной величине числа вычитается меньшее и ставится соответствующий знак
Операция умножения выполняется с использованием таблицы умножения по обычной схеме, применяемой в десятичной системе счисления с последовательным умножением множимого на очередную цифру множителя.
Пример: рассмотрим пример умножения двоичных чисел:
| ||
| 1 1 0 1 | ||
| ||
| ||
| 1 1 0 0 1 | ||
| 1 0 1 0 0 0 1 0 1 |
Примечание: умножение сводится к сдвигам множимого и сложениям.
