Расчетно-графическая работа № 2
Задача 1. Прямоугольные и полярные координаты.
- Даны концы отрезка АВ: А (1), В (5); вне отрезка АВ расположена точка С, причем ее расстояние от точки А в три раза больше расстояния от точки В. Определить координату точки С.
- Определить расстояние между точками М (3) и N (-5).
- Определить расстояние между точками Р
 и Q
и Q 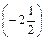 .
. - Двумя точками отрезок АВ разделили на три равные части. Определить координаты точек деления, если А (-1), В (5).
- Даны точки А (-7), В (-3). Вне отрезка АВ расположены точки C и D, причем СА = BD =
 . Определить координаты точек С и D.
. Определить координаты точек С и D. - Определить расстояние между точками А (3; 8) и В (-5, 14).
- Показать, что треугольник АВС с вершинами А (-3; -3), В (-1; 3), С (11; -1) – прямоугольный.
- Даны концы отрезка АВ: А (-2; 5), В (4; 17). На отрезке АВ расположена точка С, расстояние которой от точки А в два раза больше расстояния от точки В. Определить координаты точки С.
- Серединой отрезка АВ является точка С (2; 3). Определить координаты точки А, если В (7; 5).
- Даны вершины треугольника АВС: А
 , В
, В 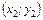 , С
, С 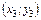 . Определить координаты точки пересечения медиан треугольника.
. Определить координаты точки пересечения медиан треугольника. - Определить площадь треугольника с вершинами А (-2; -4), В (2; 8), С (10; 2).
- Построить на координатной плоскости точки А
 , В
, В  , С
, С  , D
, D 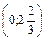 .
. - Определить расстояние между точками:
а) А (2; 3) и В (-10; -2);
б) А 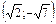 и В
и В  .
.
- Показать, что треугольник с вершинами А (2; -1), В (4; 2), С (5; 1) – равнобедренный.
- Даны вершины треугольника: А (-1; -1), В (0; -6) и С (-10; 2). Найти длину медианы, проведенной из вершины А.
- Даны концы отрезка АВ: А (-3; 7) и В (5; 11). Тремя точками отрезок разделили на четыре равные части. Определить координаты точек деления.
- Найти площадь треугольника с вершинами А (1; 5), В (2; 7), С (4; 11).
- Даны три последовательные вершины параллелограмма: А (11; 4), В (-1; -1), С (5; 7). Определить координаты четвертой вершины.
- Даны две вершины треугольника А (3; 8) и В (10; 2) и точка пересения медиан М (1; 1). Найти координаты третьей вершины треугольника.
- Даны вершины треугольника: А (7; 2), В (1; 9) и С (-8; -11). Найти расстояния точки пересечения медиан от вершин треугольника.
- Точки L (0; 0), М (3; 0) и N (0; 4) являются серединами сторон треугольника. Вычислить площадь треугольника.
- Построить точки, заданные полярными координатами: А
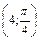 , В
, В 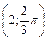 , С
, С 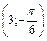 , D
, D 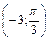 , E
, E 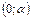 , F
, F  .
. - Найти полярные координаты точки М
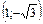 , если полюс совпадает с началом координат, а полярная ось – с положительным направлением оси абсцисс.
, если полюс совпадает с началом координат, а полярная ось – с положительным направлением оси абсцисс. - Найти прямоугольные координаты точки А
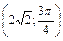 , определяемой полярными координатами, если полюс совпадает с началом координат, а полярная ось направлена по оси абсцисс.
, определяемой полярными координатами, если полюс совпадает с началом координат, а полярная ось направлена по оси абсцисс. - Построить точки А
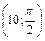 , В
, В 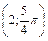 , С
, С 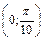 , D
, D 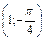 , E
, E 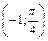 , F
, F  .
. - Даны полярные координаты точки М
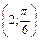 . Найти ее прямоугольные координаты, если начало координат совпадает с полюсом, а ось Ох – с полярной осью.
. Найти ее прямоугольные координаты, если начало координат совпадает с полюсом, а ось Ох – с полярной осью. - Даны полярные координаты точки М
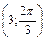 . Найти ее декартовы координаты.
. Найти ее декартовы координаты. - Определить расстояние между точками М1
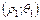 и М2
и М2 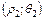 .
.
Задача 2. Прямая линия.
1. Составить уравнение прямой, отсекающей на оси координат отрезок 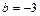 и образующей с положительным направлением оси абсцисс угол
и образующей с положительным направлением оси абсцисс угол 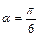 .
.
2. Составить уравнение прямой, отсекающей на осях координат отрезки 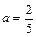 ,
,  .
.
3. Дано общее уравнение прямой  . Написать: а) уравнение с угловым коэффициентом; б) уравнение в отрезках; в) нормальное уравнение.
. Написать: а) уравнение с угловым коэффициентом; б) уравнение в отрезках; в) нормальное уравнение.
4. Построить прямые: а) 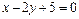 ; б)
; б)  ; в)
; в) 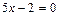 ; г)
; г) 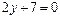 .
.
5. Дано уравнение прямой  . Написать: а) общее уравнение этой прямой; б) уравнение с угловым коэффициентом; в) уравнение в отрезках; г)нормальное уравнение.
. Написать: а) общее уравнение этой прямой; б) уравнение с угловым коэффициентом; в) уравнение в отрезках; г)нормальное уравнение.
6. Какой угол образует с положительным направлением оси абсцисс прямая 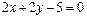 ?
?
7. Определить площадь треугольника, образованного прямой 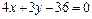 с осями координат.
с осями координат.
8. Можно ли уравнение прямой  записать в отрезках?
записать в отрезках?
9. Построить прямые: а) 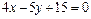 ; б)
; б) 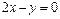 ; в)
; в) 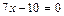 ; г)
; г) 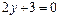 .
.
10. Составить уравнение прямой, отсекающей на оси координат отрезок 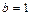 и образующей с положительным направлением оси абсцисс угол
и образующей с положительным направлением оси абсцисс угол  .
.
11. Прямая отсекает на осях координат равные положительные отрезки. Составить уравение прямой, если площадь треугольника, образованного прямой с осями координат, равна 8.
12. Составить уравнение прямой, проходящей через начало координат и точку А (-2; -3).
13. Составить уравнение прямой, проходящей через точку А (2; 5) и отсекающей на оси координат отрезок  .
.
14. Составить уравнения прямых, проходящих через точку М (-3; -4) и параллельных осям координат.
15. Составить уравнение прямой, отсекающей на осях координат равные отрезки, если длина отрезка прямой, заключенного между осями координат, равна 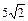 .
.
16. Определить угол между прямыми  и
и  .
.
17. Показать, что прямые 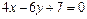 и
и 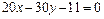 параллельны.
параллельны.
18. Показать, что прямые 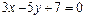 и
и 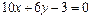 перпендикулярны.
перпендикулярны.
19. Составить уравнение прямой, проходящей через точки М (-1; 3) и N (2; 5).
20. Составить уравнение прямой, проходящей через точки А (-2; 4) и В (-2; -1).
21. Показать, что прямые 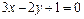 и
и 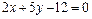 пересекаются, и найти координаты точки пересечения.
пересекаются, и найти координаты точки пересечения.
22. Определить расстояние от точки М 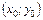 до прямой
до прямой 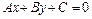 , не пользуясь нормальным уравнением прямой.
, не пользуясь нормальным уравнением прямой.
23. Определить расстояние от точки М (1; 2) до прямой 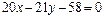 .
.
24. Дана прямая 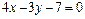 . Какие из точек А
. Какие из точек А  , В (3; 2), С (1; -1), D (0; -2), E (4; 3), F (5; 2) лежат на этой прямой.
, В (3; 2), С (1; -1), D (0; -2), E (4; 3), F (5; 2) лежат на этой прямой.
25. Составить уравнение прямой, проходящей через точку М (-2; -5) и пралллельной прямой 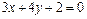
26. Даны вершины треугольника: А (2; 2), В (-2; -8) и С (-6; -2). Составить уравнение медиан треугольника.
27. Даны вершины треугольника: А (0; 1), В (6; 5) и С (12; -1). Составить уравнение высоты треугольника, проведенной из вершины С.
28. Даны стороны треугольника: 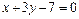 (АВ),
(АВ),  (ВС),
(ВС),  (АС). Найти длину высоты, проведенной из вершины В.
(АС). Найти длину высоты, проведенной из вершины В.
29. Определить расстояние между параллельными прямыми 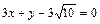 и
и 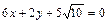 .
.
30. Составить уравнения биссектрис углов между прямыми 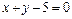 и
и 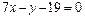 .
.
31. Даны вершины треугольника: А (1;1), В (10; 13), С (13; 6). Составить уравнение биссектрисы угла А.
32. Даны уравнения высот треугольника АВС:  ;
; 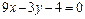 и координаты вершины А (2;2). Составить уравнения сторон треугольника.
и координаты вершины А (2;2). Составить уравнения сторон треугольника.
33. Составить уравнения прямых, проходящих через точку М (5; 1) и образующих с прямой 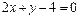 угол
угол 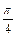 .
.
34. Найти прямую, принадлежащую пучку  и проходящую через точку М (1; 1).
и проходящую через точку М (1; 1).
Задача 3. Векторы и простейшие действия над ними
- В треугольнике АВС сторону АВ точками М и N разделили на три равные части: АМ = MN = NB. Найти вектор
 , если
, если 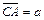 ,
, 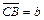 .
. - В треугольнике АВС прямая АМ является биссектрисой угла ВАС, причем точка М лежит на стороне ВС. Найти
 , если
, если  ,
, 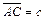 .
. - Радиусами-векторами треугольника АВС являются r1, r2 и r3. Найти радиус-вектор точки пересечения медиан треугольника.
- Найти длину вектора а = 20 i + 30 j – 60 k и его направленные косинусы.
- Найти ветор а =
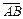 , если А (1; 2; 3) и В (5; 8; -1).
, если А (1; 2; 3) и В (5; 8; -1). - Дан треугольник АВС. На стороне ВС расположена точка М так, что
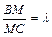 . Найти
. Найти  , если
, если  ,
, 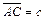 .
. - Дано
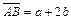 ,
, 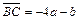 ,
, 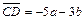 . Доказать, что АВСD – трапеция.
. Доказать, что АВСD – трапеция. - Найти проекции вектора а на оси координат, если а =
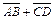 , А (0; 0; 1), В (3; 2;1), С (4; 6; 5) и D (1; 6; 3).
, А (0; 0; 1), В (3; 2;1), С (4; 6; 5) и D (1; 6; 3). - Найти длину вектора a = m i + (m + 1) j + m (m + 1) k. Показать, что треугольник АВС равносторонний.
- Даны радиусы-векторы вершин треугольника АВС: rA = i + 2 j + 3 k, rB = 3 i + 2 j + k, rC = i + 4j + k.
- Вычислить модуль вектора a = i + 2j + k -
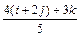 и найти его направляющие косинусы.
и найти его направляющие косинусы. - Даны точки М1 (1; 2; 3) и М2 (3; -4; 6). Найти длину и направление вектора
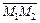 .
. - Дан вектор а = 4 i – 2 j + 3 k. Найти вектор b, если b=a, by=ay и bx= 0.
- Радиус-вектор точки М составляет с осью Оу угол 600, а с осью Oz угол 450; длина его r = 8. Найти координаты точки М, если абсцисса ее отрицательна.






