Тема 4. ГРАФЫ И СЕТИ
Способы задания графов
Теория.
1. Графическим изображением.
2. Множеством вершин и дуг: совокупностью двух множеств — непустого множества V (множества вершин) и множества Е неупорядоченных пар различных элементов множества V (Е — множество ребер)
3. Матрицей инцидентности 
размера 
: по вертикали и горизонтали указываются вершины и ребра соответственно, а на пересечении i -й вершины и j -го ребра в случае неориентированного графа записывается 1, если они инцидентны, и 0 – в противном случае, т.е.
В случае орграфа на пересечении i -й вершины и j -го ребра записывается минус единица (-1), если вершина является началом ребра и единица (+1) если вершина является концом ребра; 0 – записывается, если вершина и ребро не инцидентны. Если некоторая вершина является для ребра и началом, и концом (т.е. ребро – петля), проставляется любое другое число, например 2, т.е.
где 
любое число, отличное от -1, 1. 0.
4. Списком ребер графа, представленным двумя столбцами: в левом перечисляются все ребра 
, а в правом – инцидентные ему вершины vij. Для н-графа порядок вершин в строке произволен, для орграфа первым стоит номер начала ребра;
5. Матрицей смежности 
–квадратной матрицей размера 
, гдепо вертикали и горизонтали перечисляются все вершины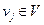 
,а на пересечении k-й и l-й вершин в случае н-графа проставляется число, равное числу ребер, соединяющих эти вершины. Для орграфа 
равно числу ребер с началом в k-й вершине и концом в l-й.
Пример 1. Задать сетевой граф, изображенный на рис. 1 различными способами.
Рис 1.
Решение:
1. Графическое задание представлено на рисунке.
2. Множеством вершин и дуг:
V={1,2,3,4,5,6}, E={(1,2),(1,3),(2,4),(2,5),(3,4),(4,6),(5,6)}.
3. Матрицей инцидентности:
Таблица 1
| G | a | b | c | d | e | f | g |
| -1 | -1 | ||||||
| -1 | -1 | ||||||
| -1 | |||||||
| -1 | |||||||
| -1 | |||||||
4. Матрицей смежности:
Таблица 2
| G | ||||||
5. Списком ребер:
Таблица 3
| Ребро | Вершины |
| a | 1,2 |
| b | 1,3 |
| c | 3,4 |
| d | 2,4 |
| e | 2,5 |
| f | 5,6 |
| g | 4,6 |
Пример 2. Построить графическое изображение графа заданного матрицей инцидентности вида:
Таблица 4
| G | I | II | III | IV | V | VI | VII |
Решение.
При наличии матрицы инцидентности число всех вершин и число ребер графа определяется очевидным образом по размеру матрицы: число ребер графа |E| равно числу строк m, а число вершин |V| – числу столбцов n матрицы. В данном примере m=11, n=7.
Граф выглядит следующим образом:
Рис. 2
Пример 3. Построить графическое изображение орграфа заданного матрицей смежности вида:
Таблица 5
| G | I | II | III | IV | V | VI | VII |
| I | |||||||
| II | |||||||
| III | |||||||
| IV | |||||||
| V | |||||||
| VI | |||||||
| VII |
Решение.
По матрице смежности определим число вершин графа определяется порядком n матрицы. В данном примере n=7. Число ребер орграфа определяется всеми элементами 
матрицы смежности. Отсюда их число равно:
=10.
Граф выглядит следующим образом:
Рис. 3
Пример 4. Построить графическое изображение двух графов G1 и G2 заданных списками своих ребер вида:
Таблица 6 Таблица 7
| G1 | G2 | |||
| Ребро | Вершины | Ребро | Вершины | |
| a | 1,2 | a | 1,2 | |
| b | 2,2 | b | 2,3 | |
| c | 2,3 | c | 3,4 | |
| d | 3,3 | d | 4,5 | |
| e | 3,5 | e | 1,1 | |
| f | 1,4 | f | 1,5 | |
| g | 4,5 | g | 5,5 |
Решение.
Количество вершин равно 5, количество ребер равно 7. Графы выглядят следующим образом:
Рис. 4 Рис. 5
Преобразования описаний графа
Теория.
Построение матрицы инцидентности по списку ребер. Каждая строка списка соответствует строке матрицы с тем же номером. Для н-графа в строке списка указаны номера элементов строки матрицы инцидентности, равные 1. Для орграфа в этой строке первым стоит номер элемента строки матрицы, равного -1, а вторым – номер элемента, равного 1. При совпадении номеров в строке списка ребер в названном элементе строки матрицы инцидентности проставляется, например, 2.
Построение по матрице смежности списка ребер. Элементу матрицы, расположенному в i -й строке и j -ом столбце, соответствует строк списка ребер (при = 0 – ни одной строки), в каждой из которых записаны номера i, j. Для н-графа эти строки соответствуют только элементам верхнего правого треугольника матрицы смежности, т.е. элементам 
, а для орграфа нужно рассматривать все элементы .
Матрица смежности н-графа симметрична относительно главной диагонали 
, и все его ребра определяются верхним правым треугольником матрицы, расположенным над диагональю, включая последнюю. Таким образом, число ребер н-графа по матрице смежности равно сумме элементов , расположенных на диагонали и выше, т.е. равно:
.
Ребра орграфа определяются всеми элементами матрицы смежности, отсюда их число равно:
Список ребер графа является, по существу, сокращенным представлением матрицы инцидентности (в каждой ее строке только два элемента отличны от 0 или даже один, если ребро – петля).
Пример 5. Построить матрицу инцидентности н-графа по списку ребер вида:
Таблица 8
| Ребро | Вершины |
| A,B | |
| A,C | |
| B,D | |
| A,E | |
| C,D | |
| C,D | |
| D,D | |
| C,E | |
| D,G | |
| E,F | |
| F,G |
Решение.
Количество вершин равно 7, количество ребер равно 11. Таким образом, матрица инцидентности будет иметь 7 столбцов и 11 строк.
Таблица 9
| G | A | B | C | D | E | F | G |
Матрица инцидентности (таблица 9) совпадает с таблицей инцидентности (таблица 4) и граф, описанный данной таблицей, может иметь вид рис. 2.
Пример 6. Построить список ребер графа по матрице смежности вида:
Таблица 10
| G | |||||
Решение.
Количество вершин графа равно числу строк и столбцов матрицы и равно 5, а количество ребер вычисляется по формуле
=7.
Обозначим ребра буквами латинского алфавита. Тогда список ребер графа будет имеет следующий вид:
Таблица 11
| G1 | |
| Ребро | Вершины |
| a | 1,2 |
| b | 2,2 |
| c | 2,3 |
| d | 3,3 |
| e | 3,5 |
| f | 1,4 |
| g | 4,5 |
Данная таблица соответствует списку ребер (таблица 6) графа изображенного на рис. 4.
