–озпод≥льна л≥н≥€ 10 к¬ Ц кабельна. ћатер≥ал жил кабелю Ц алюм≥н≥й. абел≥ прокладають в земл€них транше€х. —хема розпод≥льноњ л≥н≥њ (рис. 2.1) Ц петльова, дл€ забезпеченн€ резервуванн€ живленн€ кожноњ “ѕ (ј“ѕ).
ќсоблив≥стю розпод≥льних мереж Ї њхн€ експлуатац≥€ за роз≥мкнутою схемою. ѕо€снюЇтьс€ це тим, що електрична мережа з одноб≥чним живленн€м може бути реал≥зована значно дешевше, н≥ж ≥з двосторонн≥м живленн€м. ” мереж≥ з одноб≥чним живленн€м Ї можлив≥сть встановлювати менше вимикач≥в ≥ використовувати пор≥вн€но простий релейний захист. р≥м того, в роз≥мкнутих мережах силове ≥ комутац≥йне устаткуванн€ вибирають б≥льш легким у пор≥вн€нн≥ ≥з замкнутими мережами, за рахунок зменшенн€ струм≥в короткого замиканн€ ( «).
“аблиц€ 2.3 Ц Ќавантаженн€ “ѕ ≥ ном≥нальна потужн≥сть трансформатор≥в
| –озрахунков≥ дан≥ | ”мовн≥ позначенн€ | ѕ≥дстанц≥€ | |||
| ј“ѕ-1 | ј“ѕ-2 | “ѕ-3 | “ѕ-4 | ||
| Ќавантаженн€ “ѕ (ј“ѕ) з≥ сторони ЌЌ, к¬т | – тп | ||||
| ѕовне навантаженн€ “ѕ (ј“ѕ) з≥ сторони ЌЌ, к¬·ј | S тп | ||||
| Ќом≥нальна потужн≥сть трансформатор≥в п≥дстанц≥њ, кв·ј | S т ном | ||||
| «авантаженн€ трансформатор≥в: у нормальному режим≥ | 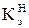
| ||||
| у п≥сл€авар≥йному режим≥ | 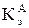
| ||||
| јктивне навантаженн€ п≥дстанц≥њ з≥ сторони ¬Ќ, к¬т | 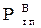
|
ѕетльова схема 10 к¬ експлуатуЇтьс€ у вигл€д≥ двох нап≥впетель, €к≥ отримують шл€хом розмиканн€ одн≥Їњ з д≥л€нок кабельноњ мереж≥. ¬ €кост≥ критер≥€, за €ким визначають д≥л€нку, €ку потр≥бно в≥дключити, приймають м≥н≥мум втрат потужност≥ в схем≥ при нормальн≥й њњ робот≥. ѕриродний потокорозпод≥л в замкнут≥й кабельн≥й мереж≥ зб≥гаЇтьс€ з економ≥чним потокорозпод≥лом, €кий характеризуЇтьс€ м≥н≥мальними втратами потужност≥. « одного боку, петльову схему бажано експлуатувати замкнутою дл€ зниженн€ втрат потужност≥, з ≥ншого боку, њњ потр≥бно розмикати за умовами експлуатац≥њ.
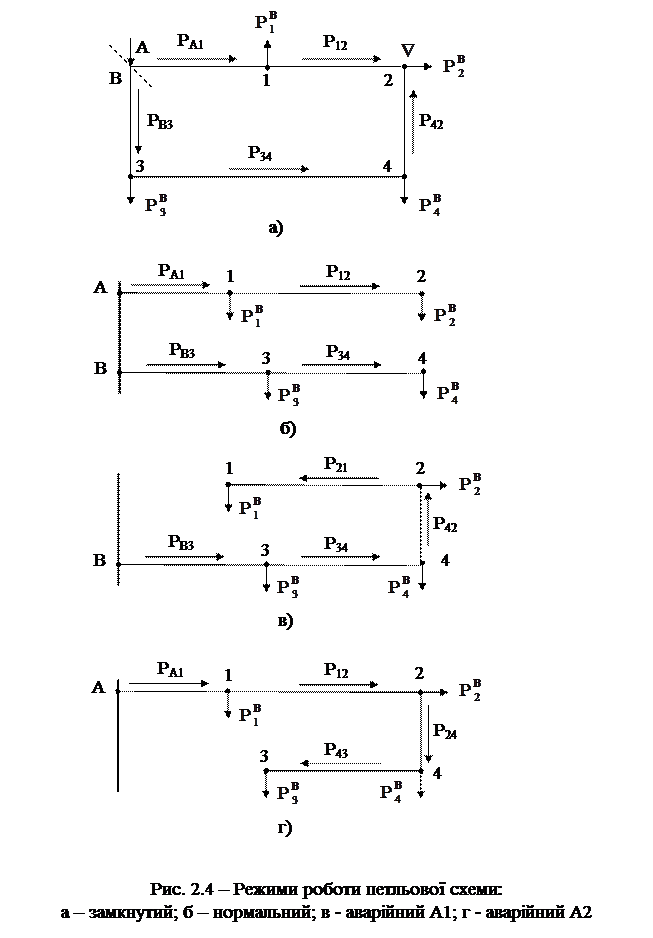
«в≥дки висновок: схему варто розмикати таким чином, щоб потокорозпод≥л роз≥мкнутоњ мереж≥ €кнайменше в≥др≥зн€вс€ в≥д природного потокорозпод≥лу в замкнут≥й мереж≥. ÷е дос€гаЇтьс€ шл€хом розмиканн€ мереж≥ в точц≥ потокорозпод≥лу з боку надходженн€ меншоњ потужност≥. ƒл€ визначенн€ д≥л€нки, €ку потр≥бно в≥дключити, робитьс€ розрахунок потокорозпод≥лу в замкнут≥й петльов≥й схем≥ (рис. 2.4, а). –озрахунок виконують дл€ навантажень “ѕ ≥ ј“ѕ, приведених до сторони ¬Ќ трансформатор≥в (табл. 2.3).
–озрахунок потокорозпод≥лу в петльов≥й схем≥ виконують в наступному пор€дку. —початку визначають потужн≥сть на одн≥й з головних д≥л€нок, Ђј-1ї чи Ђ¬-3ї, за формулою, що в≥дпов≥даЇ ц≥й д≥л€нц≥:
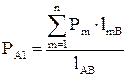 ; (2.16)
; (2.16)
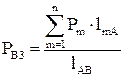 , (2.17)
, (2.17)
де –ј1 ≥ –¬3 Ц потужн≥сть, що прот≥каЇ на головних д≥л€нках, к¬т; lmј ≥ lm¬ Ц довжина л≥н≥њ в≥д точки m, в €к≥й включене навантаженн€ –m, до пункту живленн€ ј ≥ ¬ в≥дпов≥дно; lј¬ Ц повна довжина петльовоњ л≥н≥њ, км; 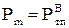 Ц активне навантаженн€ п≥дстанц≥њ m на сторон≥ ¬Ќ, к¬т.
Ц активне навантаженн€ п≥дстанц≥њ m на сторон≥ ¬Ќ, к¬т.
|
|
|
ѕ≥сл€ визначенн€ потужност≥, що прот≥каЇ на головн≥й д≥л€нц≥, знаход€ть потужност≥ на ≥нших д≥л€нках петльовоњ л≥н≥њ за допомогою першого закону ≥рхгофа, посл≥довно застосовуючи його дл€ кожноњ точки включенн€ навантаженн€. Ќаприклад, €кщо розрахунок виконаний за формулою (2.16) дл€ головноњ д≥л€нки Ђј-1ї, то дал≥ робл€ть так≥ обчисленн€:
–12 = –ј1 Ц 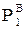 ; –24 = –12 Ц
; –24 = –12 Ц 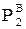 < 0; –43 = –24 Ц
< 0; –43 = –24 Ц 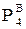 < 0; –3¬ = –43 Ц
< 0; –3¬ = –43 Ц 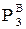 < 0.
< 0.
ќдне ≥з значень потужностей, що прот≥кають по д≥л€нках мереж≥, обов'€зково вийде негативним, наприклад, –24 < 0. ”с≥ наступн≥ потужност≥ також будуть негативними. ÷е означаЇ, що встановлено вузол, в €кий потужн≥сть надходить ≥з двох стор≥н (точка потокорозпод≥лу Ц Ñ), у даному приклад≥ вузол Ђ2ї.
“реба виконати перев≥рку розрахунку потокорозпод≥лу. ƒл€ цього, зокрема в розгл€нутому приклад≥, треба розрахувати –¬3 за формулою (2.17) ≥ переконатис€ у в≥дпов≥дност≥ значенню, отриманому по балансах у вузлах (–¬3 ≈ Ц –3¬).
¬иб≥р перер≥з≥в кабелю на д≥л€нках петльовоњ схеми. ѕерер≥зи кабелю вибирають за тривалим припустимим струмом в нормальному ≥ п≥сл€авар≥йних режимах з наступною перев≥ркою за економ≥чною щ≥льн≥стю струму в нормальному режим≥ ≥ припустимому в≥дхиленню напруги.
–озпод≥л схеми робл€ть шл€хом в≥дключенн€ л≥н≥њ, по €к≥й до точки потокорозпод≥лу надходить менша потужн≥сть. ” розгл€нутому приклад≥, коли точка потокорозпод≥лу знаходитьс€ у вузл≥ 2 (рис. 2.4, а), припустимо, що –12 > –42. “од≥ дл€ пост≥йноњ експлуатац≥њ мереж≥ варто в≥дключити д≥л€нку Ђ2-4ї (рис. 2.4, б). ” раз≥ протилежноњ нер≥вност≥ (–12 < –42), в≥дключати треба було б д≥л€нку Ђ1-2ї. «а такою схемою розраховують дв≥ нап≥впетл≥ розпод≥льноњ л≥н≥њ 10 к¬ у нормальному режим≥.
” п≥сл€авар≥йних режимах розгл€дають по черз≥ два можливих найб≥льш складн≥ випадки:
1) вих≥д з ладу головноњ д≥л€нки в пункт≥ живленн€ ј (рис. 2.4, в);
2) вих≥д з ладу головноњ д≥л€нки в пункт≥ живленн€ ¬ (рис. 2.4, г).
–озрахунок л≥н≥њ в п≥сл€авар≥йному режим≥ ведуть з урахуванн€м того, що вс≥ п≥дстанц≥њ петл≥ одержують живленн€ в≥д одного з пункт≥в (¬ чи ј).
ѕор€док розрахунку. ” нормальному режим≥ визначають потоки активноњ потужност≥ на кожн≥й з д≥л€нок нап≥впетель мереж≥ 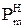 , починаючи з к≥нц€ роз≥мкнутоњ л≥н≥њ. ¬раховують коеф≥ц≥Їнт сум≥щенн€ розрахункових максимум≥в активних навантажень п≥дстанц≥й ћ. ƒл€ д≥л€нки m
, починаючи з к≥нц€ роз≥мкнутоњ л≥н≥њ. ¬раховують коеф≥ц≥Їнт сум≥щенн€ розрахункових максимум≥в активних навантажень п≥дстанц≥й ћ. ƒл€ д≥л€нки m
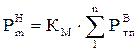 , (2.18)
, (2.18)
де n Ц к≥льк≥сть “ѕ (ј“ѕ), що одержують живленн€ через д≥л€нку m.
–екомендуЇтьс€ в розрахунковому завданн≥ дл€ n = 1 прийн€ти ћ = 1; дл€ n = 2 Ц ћ = 0,85; дл€ n ≥ 3 Ц ћ = 0,9.
ƒл€ нашого прикладу (рис. 2.4, б):
–12 = 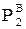 ; –ј1 = 0,85 · (
; –ј1 = 0,85 · (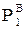 +
+ 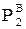 );
);
–34 = 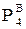 ; –¬3 = 0,85 · (
; –¬3 = 0,85 · (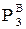 +
+ 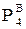 ).
).
ѕотоки потужност≥ нанос€ть на схему мереж≥ ≥, €к ус≥ наступн≥ розрахунки, внос€ть у табл. 2.4.
–озраховують струм кожноњ д≥л€нки Ђmї мереж≥, ј:
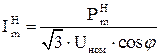 , (2.19)
, (2.19)
де Uном = 10 к¬ Ц ном≥нальна напруга мереж≥; cosj = 0,9 Ц середнЇ значенн€ коеф≥ц≥Їнта потужност≥ навантаженн€.
«наход€ть перер≥з жили кабел≥в у нормальному режим≥ 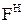 з огл€ду на наступне:
з огл€ду на наступне:
Ц у м≥ських розпод≥льних мережах 10 к¬ перер≥з кабел≥в з алюм≥н≥Ївими жилами при прокладц≥ њх у земл€них транше€х сл≥д приймати не менше 35 мм2, у кожн≥й л≥н≥њ допускаЇтьс€ не б≥льше трьох р≥зних перер≥з≥в;
Ц довгострокове припустиме струмове навантаженн€ на кабель (див.
табл. ѕ.2) повинне бути не менше струмового розрахункового навантаженн€ д≥л€нки 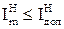 ;
;
|
|
|
Ц перер≥з жили кабелю, в≥дключеного при розмиканн≥ мереж≥, сд≥д приймати р≥вним перер≥зу жили кабелю т≥Їњ сум≥жноњ д≥л€нки, на €к≥й перер≥з менше.
¬изначають завантаженн€ кабелю в нормальному режим≥ на кожн≥й д≥л€нц≥:
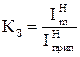 . (2.20)
. (2.20)
“аблиц€ 2.4 Ц ¬иб≥р перер≥з≥в жил кабел≥в розпод≥льноњ л≥н≥њ 10 к¬
| –озрахунков≥ дан≥ | ”мовне позначенн€ | ƒ≥л€нка л≥н≥њ | ||||
| ј-1 | 1-2 | 2-4 | 3-4 | ¬-3 | ||
| ƒовжина д≥л€нки, км | L | |||||
| ѕот≥к активноњ потужност≥ на д≥л€нц≥ Ђmї у нормальному режим≥, к¬т | 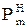
| |||||
| —трум на д≥л€нц≥ Ђmї у нормальному режим≥, ј | 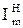
| |||||
| ѕерер≥з жили кабелю, €кий обрано за нормальним режимом, мм2 | 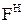
| |||||
| ѕрипустиме струмове навантаженн€ на кабель, €кий обрано за нормальним режимом, ј | 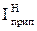
| |||||
| «авантаженн€ кабелю в нормальному режим≥ | 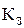
| |||||
| ѕрипустиме струмове навантаженн€ на кабель у п≥сл€авар≥йному режим≥, ј | 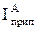
| |||||
| ѕот≥к активноњ потужност≥ на д≥л€нц≥ Ђmї у п≥сл€авар≥йному режим≥ 1 (пошкоджено ј - 1), к¬т | 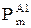
| |||||
| —трум навантаженн€ д≥л€нки Ђmї у п≥сл€авар≥йному режим≥ 1, ј | 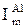
| |||||
| ѕот≥к активноњ потужност≥ на д≥л€нц≥ Ђmї у п≥сл€авар≥йному режим≥ 2 (пошкоджено ¬ - 3), к¬т | 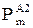
| |||||
| —трум навантаженн€ д≥л€нки Ђmї у п≥сл€авар≥йному режим≥ 2, ј | 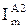
| |||||
| ѕерер≥з жили кабелю по струму навантаженн€ в п≥сл€авар≥йному режим≥, мм2 | 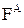
| |||||
| ≈коном≥чно виг≥дний перер≥з жили кабелю, мм2 |  F ек F ек
| |||||
| ѕерер≥з жили кабел≥в з урахуванн€м перер≥з≥в, обраних у нормальному ≥ п≥сл€авар≥йних режимах ≥ за економ≥чною щ≥льн≥стю струму, мм2 | F | |||||
| ¬трата напруги в кожн≥й д≥л€нц≥ в нормальному режим≥, ¬ | 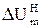
| |||||
| ¬трата напруги в нормальному режим≥ до найб≥льш в≥ддаленоњ “ѕ, % | 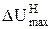
| |||||
| ¬трата напруги в кожн≥й д≥л€нц≥ в п≥сл€авар≥йному режим≥ 1, ¬ | 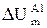
| |||||
| ¬трата напруги до найб≥льш в≥ддаленоњ “ѕ у п≥сл€авар≥йному режим≥ 1, % | 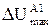
| |||||
| ¬трата напруги в кожн≥й д≥л€нц≥ в п≥сл€авар≥йному режим≥ 2, ¬ | 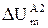
| |||||
| ¬трата напруги до найб≥льш в≥ддаленоњ “ѕ у п≥сл€авар≥йному режим≥ 2, % | 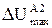
|
–озраховують припустиме струмове навантаженн€ в п≥сл€авар≥йному режим≥ на кабель, перер≥з €кого обрано за нормальним режимом, ј:
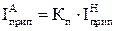 , (2.21)
, (2.21)
де п = 1,25 Ц коеф≥ц≥Їнт, €кий враховуЇ припустиме перевантаженн€ кабел≥в на пер≥од максимуму навантаженн€, р≥вний 3 години за добу (прот€гом 5 д≥б), €кщо тривале завантаженн€ кабелю « перед його перевантаженн€м не перевищувало 0,8.
¬изначають пот≥к активноњ потужност≥ 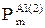 , к¬т ≥ струм навантаженн€
, к¬т ≥ струм навантаженн€ 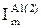 , ј, на д≥л€нках л≥н≥њ в п≥сл€авар≥йних режимах 1 ≥ 2:
, ј, на д≥л€нках л≥н≥њ в п≥сл€авар≥йних режимах 1 ≥ 2:
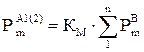 ; (2.22)
; (2.22)
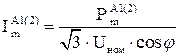 . (2.23)
. (2.23)
ѕерев≥р€ють перер≥з жили кабелю 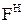 по струму на кожн≥й д≥л€нц≥ Ђmї у п≥сл€авар≥йних режимах
по струму на кожн≥й д≥л€нц≥ Ђmї у п≥сл€авар≥йних режимах 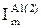 , виход€чи з того, що
, виход€чи з того, що
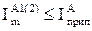 .
.
ѕри необх≥дност≥ зб≥льшують ран≥ше обраний перер≥з жили кабелю 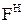 до перер≥зу
до перер≥зу 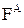 , що в≥дпов≥даЇ струму навантаженн€ п≥сл€авар≥йних режим≥в
, що в≥дпов≥даЇ струму навантаженн€ п≥сл€авар≥йних режим≥в 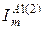 .
.
¬изначають перер≥з кабелю кожноњ д≥л€нки за економ≥чною щ≥льн≥стю струму, мм2:
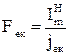 , (2.24)
, (2.24)
де j ек Ц економ≥чна щ≥льн≥сть струму, ј / мм2 (див. табл. ѕ.3).
ќтримане значенн€ Fек округл€ють до стандартного найближчого перер≥зу.
ѕерер≥з жили кабелю F приймають найб≥льшим з отриманих ран≥ше значень, обраних:
|
|
|
Ц за струмом дл€ нормального режиму (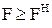 );
);
Ц за струмом в п≥сл€авар≥йних режимах (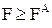 );
);
Ц за економ≥чною щ≥льност≥ струму jек (F ³ Fек).
” зв'€зку з в≥дсутн≥стю вих≥дних даних перев≥рку обраного перер≥зу кабелю по струму « в розрахунковому завданн≥ не провод€ть.
¬изначають дл€ нормального режиму втрату напруги в кожн≥й з д≥л€нок л≥н≥њ, ¬:
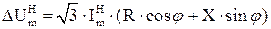 , (2.25)
, (2.25)
де R ≥ ’ Ц активний ≥ ≥ндуктивний опори кабелю (табл. ѕ.4); cosj = 0,9.
–озраховують дл€ нормального режиму максимальну втрату напруги (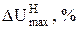 ), в кожн≥й нап≥впетл≥ розпод≥льчоњ л≥н≥њ в≥д шин ƒ∆ до найб≥льш в≥ддаленоњ “ѕ:
), в кожн≥й нап≥впетл≥ розпод≥льчоњ л≥н≥њ в≥д шин ƒ∆ до найб≥льш в≥ддаленоњ “ѕ:
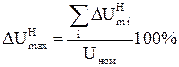 . (2.26)
. (2.26)
јналог≥чно визначають дл€ двох п≥сл€авар≥йних режим≥в втрату напруги в кожн≥й з д≥л€нок л≥н≥њ, використовуючи в≥дпов≥дно струм навантаженн€ 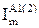 , ≥ знаход€ть максимальн≥ втрати напруги (
, ≥ знаход€ть максимальн≥ втрати напруги (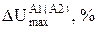 ), у л≥н≥њ в≥д шин ƒ∆ до найб≥льш в≥ддаленоњ “ѕ.
), у л≥н≥њ в≥д шин ƒ∆ до найб≥льш в≥ддаленоњ “ѕ.
ѕрипустим≥ величини втрати напруги в нормальному режим≥
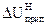 = 6% [5, 6], у п≥сл€авар≥йному Ц прийн€ти
= 6% [5, 6], у п≥сл€авар≥йному Ц прийн€ти 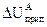 = 11%.
= 11%.
Ќеобх≥дн≥ дл€ виконанн€ розрахункового завданн€ 1 дов≥дков≥ дан≥ наведен≥ в табл. ѕ.1 Ц ѕ.4.
–ќ«–ј’”Ќ ќ¬≈ «ј¬ƒјЌЌя 2
ѕостановка завданн€
Ќа рис. 3.1 наведен≥ однол≥н≥йн≥ схеми двохобмоточного (рис. 3.1, а), трьохбмоточного (рис. 3.1, б) трансформатор≥в ≥ автотрансформатора (рис. 3.1, в).
 |
–ис. 3.1 Ц ќднол≥н≥йн≥ схеми трансформатор≥в:
а) двохобмоточного; б) трьохбмоточного; в) автотрансформатора
ѕри виконанн≥ завданн€ потр≥бно зробити розрахунок:
1) двохбмоточного трансформатора;
2) трьохбмоточного трансформатора чи автотрансформатора залежно в≥д вих≥дних даних.
” ход≥ розрахунку необх≥дно:
- визначити параметри повноњ ≥ спрощеноњ схем зам≥щенн€ трансформатор≥в;
- визначити втрати електроенерг≥њ у трансформаторах при заданому навантаженн≥.
¬ар≥ант вих≥дних даних (табл. 3.1 ≥ 3.2 графи Ђвар≥антї) приймають в≥дпов≥дно до пор€дкового номера студента в журнал≥ академ≥чноњ групи. ¬ар≥анти в≥др≥зн€ютьс€ типом трансформатора ≥ величиною навантаженн€ з≥ стор≥н ЌЌ ≥ середньоњ напруги (—Ќ).






