Функціональна схема задачі:
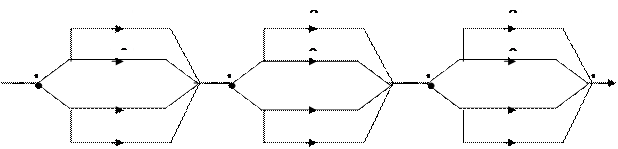
Етап 1.
Оскільки немає необхідності розраховувати прибуток окремо, то матимемо формулу для розрахунку максимальних ресурсів, що вкладатимуться в купівлю нового обладнання.
к2 =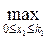 
((a– b+g-q) х1 + (b– q) к1) =
= 
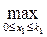((0,4– 0,42+0,7–0,6)х1 + (0,42+ 0,6)к1) =
= 
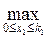(0,08х1 + 1,02 к1) = 1,1 к1
Як видно з останнього запису, - для отримання максимального прибутку від експлуатації обладнання в першому році, необхідно вкладати ресурси в обладнання І-го типу.
Етап 2.
Розраховуємо кошти, які вкладаються для купівлі нового обладнання на 3-ій рік:
к3 =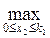 
((0,4-0,42+0,7–0,6)х2 + (0,42 + 0,6)к2) =
= 
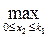(0,08х2 + 1,02 к2) = 1,1 к2 = 
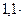1,1 к1 = 1,21 к1
Залишки після трьох років діяльності підприємства складатимуть:
f3 = к4 = 1,1 к3 = 1,331 к1
Висновок: вкладаючи кошти для купівлі обладнання І-го типу, підприємство буде з прибутком.
3. Задача розподілу ресурсів за умови вкладання отриманих прибутків в розвиток автотранспортних підприємстві і відрахування прибутків на певних етапах їх діяльності.
Задамо вхідні параметри: a = 0,8; b = 0,75; g = 0,4; q = 0,5, Т= 3.
Сума прибутку, що отримується після 1-го і 3-го років, вкладається в розвиток підприємств, а після 2-го – відраховується до головного підприємства (залишок після останнього року до прибутку не додається). Шукаємо умовне оптимальне управління, починаючи з 3-го року.
 | |||
 | |||
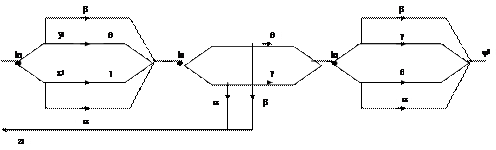Знайдемо умовне оптимальне управління, тобто підрахуємо залишки після кожного року діяльності підприємств, починаючи з третього року.
Етап 1.
f3 = aх3 + b(к3 – х3) + gх3 + q (к3-х3) = (a– b+g – q)х3 + (b+q)к3;
f3max=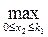 
((0,8-0,75+0,4– 0,5)х3+(0,75+0,5)к3)= 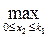(– 0,05х3+1,25к3) = 1,25к3
При таких вхідних параметрах другому підприємству потрібно віддати всі ресурси, а перше залишити без дотацій: х3 = 0, у3 = к3 і z3 = 0.
Етап 2.
f2 º к3 = (g– q)х2 + q к2 = (0,4 – 0,5)х2 + 0,5к2 = – 0,1х2 + 0,5к2
z2 = (a– b)x2 + bк2 = 0,05х2 + 0,5к2
z2max =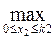 
(0,05x2 + 0,75к2) = 0,8к2
Щоб отримати максимальний прибуток, необхідно в перше підприємство вкласти всі ресурси, а в друге – нічого: х2 = к2, у2 = 0.
Етап 3.
f1 º к2 =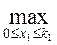 
(– 0,05х1 + 1,25к1) = 1,25к1
z1 = 0; x1 = 0; y1 = к1, тобто всі ресурси вкладатимуться в 2-е підприємство на першому році їх діяльності.
Висновок: при такому розподілі ресурсів підприємства матимуть прибуток після першого року діяльності, рівний 1,25 від початкового вкладу (К= к1), який повністю вкладається в 1-е підприємство, і отриманий в кінці 2-го року прибуток, рівний
z2max = 0,8к2 =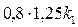 
= к1 = К,
тобто рівний величині ресурсів, вкладених в обидва підприємства на початку планового періоду, відраховується до головного підприємства. Залишки після 2-го року діяльності підприємств, рівні
f2 = к3 = – 0,1х2 + 0,5к2 = – 0,1к2 + 0,5к2 =0,4к2 = 0,4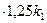 
= 0,5к1 = 0,5К,
вкладаються в перше підприємство. Після 3-го року прибуток вкладається у виробництво 2-го підприємства і разом із залишками складатимуть суму, рівну
f3 = 1,25к3 = 1,25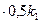 
= 0,625К.
Самостійні завдання
Самостійні завдання, що пропонуються, з дисципліни "Основи теорії систем та системного аналізу" мають на меті краще засвоєння матеріалу відповідного курсу лекцій. Завдання складаються з трьох розділів, які виконуються поступово при вивченні студентами відповідного розділу.
Самостійні завдання стосуються питань загальної теорії систем і математичних моделей, що їм відповідають.
1. Завдання на побудову математичних регресійних моделей систем. Завдання складається з двох задач і передбачає отримання лінійних математичних моделей систем за результатами експериментальних досліджень. Кількість отриманих пар значень змінних входу та змінної виходу дорівнює 7 і залишається незмінною для всіх варіантів.
Задача 1. Були проведені експериментальні дослідження впливу розмірів інвестицій в розвиток виробництва підприємства (x1 в тис. гривень) та основних фондів підприємства (x2 в тис. грн.) на отриманий річний прибуток (y в тис. грн.). Аналіз було здійснено за показниками сімох підприємств приблизно однакового роду діяльності.
Дані експериментальних досліджень приведені в таблицях варіантів.
Варіант 1
| y: 960 1260 610 590 900 820 880 |
| x1 : 18 14 6 1 9 6 12 |
| x2 : 60 180 80 120 100 170 110 |
Варіант 2
| y: 1090 750 780 950 800 500 850 |
| x1: 40 7 6 15 20 3 9 |
| x2: 170 70 95 120 90 60 90 |
Варіант 3
| y: 1020 800 1130 740 180 800 960 |
| x1 : 17 12 16 6 12 15 18 |
| x2: 105 90 115 90 70 80 100 |
Варіант 4
| y: 960 900 1130 590 890 830 880 |
| x1: 18 7 16 1 7 15 12 |
| x2 : 60 160 110 120 140 80 110 |
Варіант 5
| y: 1260 1200 800 720 1060 920 990 |
| x1: 14 14 1 1 3 10 2 |
| x2 : 180 180 90 80 130 110 120 |
Варіант 6
| y: 1290 750 780 950 800 500 850 |
| x1: 43 6 5 17 20 3 9 |
| x2: 170 70 95 120 90 60 90 |
Варіант 7
| y: 960 760 980 800 860 610 590 |
| x1: 18 3 12 15 7 6 1 |
| x2: 60 220 160 80 160 80 120 |
Варіант 8
| y: 860 590 800 920 900 700 880 |
| x1: 18 1 12 14 15 6 15 |
| x2: 60 120 80 170 120 90 80 |
Варіант 9
| y 1160 800 720 810 790 990 700 |
| x1: 14 2 1 3 7 13 1 |
| x2: 180 90 80 110 100 170 110 |
Варіант 10
| y: 800 700 710 1020 620 850 870 |
| x1: 3 2 5 14 3 5 12 |
| x2: 82 105 66 110 60 108 70 |
В цій задачі необхідно:
а) отримити чисельні значення коефіцієнтів b0 та b1 лінійної регресійної моделі: y = b0 + b1x1, тобто визначити залежність прибутку від розмірів капіталовкладень підприємства. При цьому дані про x2 не беруться до уваги;
б) середню квадратичну похибку моделі;
в) коефіцієнт кореляції експериментальних даних з лінійною моделлю;
г) в довільному масштабі представити графік функції y(x1) на фоні кореляційного поля отриманих експериментальних точок.
Зробити необхідні висновки, де пояснити фізичний зміст b0 та b1, а також роль і значення коефіцієнта кореляції R.
Задача 2. Розрахувати параметри нелінійної регресії, скориставшись таблицею приведення нелінійної форми функціональної залежності до лінійної.
Вихідні дані до задачі. Нумерація даних для функцій відповідає їх нумерації в таблиці, значення х для всіх прикладів однакове:
х1 = 1; х2 = 2; х3 = 3,5; х4 = 5;
2. у1 = 0,1; у2 = 0,05; у3 = 0,027; у4 = 0,02;
3. у1 = 10,3; у2 = 5; у3 = 3; у4 = 2,4;
4. у1 = 0,17; у2 = 0,18; у3 = 0,19; у4 = 0,192;
5. у1 = 2; у2 = 4; у3 = 11; у4 = 31;
6. у1 = 17,4; у2 = 53; у3 = 1040; у4 = 20300;
7. у1 = 3; у2 = 5; у3 = 10; у4 = 20;
8. у1 = 2,1; у2 = 4,2; у3 = 7,7; у4 = 9,3;
9. у1 = 1; у2 = 4; у3 = 12; у4 = 25;
10. у1 = 1; у2 = 1,6; у3 = 2,1; у4 = 2,4;
11. у1 = 1; у2 = 2,4; у3 = 3,5; у4 = 4,2;
12. у1 = 3,3; у2 = 2,5; у3 = 1,8; у4 = 1,4;
13. у1 = 3,33; у2 = 5; у3 = 6,36; у4 = 7,14;
14. у1 = 74; у2 = 27; у3 = 17; у4 = 15;
15. у1 = 500; у2 = 50; у3 = 19; у4 = 13;
16 у1 = 2,1; у2 = 2,28; у3 = 2,65; у4 = 3,12, n = 1,5 (показник степені х).
Побудувати графіки отриманих моделей.
Скористатися наступною таблицею для представлення нелінійної форми функцій у вигляді лінійної і подальшим переходом до попередніх параметрів регресії.
| № | Функція у(х) | х′ | у′ | а | b |
| y = a + bx | x | y | a′ | b′ | |
| y = 1/(a + bx) | x | 1/y | a′ | b′ | |
| y = a + b/x | 1/x | y | a′ | b′ | |
| y = x/(a + bx) | x | x/y | a′ | B′ | |
| y = abx | x | lg y | 10a′ | 10b′ | |
| y = aebx | x | ln y | ea′ | b′ | |
| y = a10bx | x | lg y | 10a′ | b′ | |
| y = 1/(a + be-x) | e-x | 1/y | a′ | b′ | |
| y = axb | lg x | lg y | 10a′ | b′ | |
| y = a + b lgx | lg x | y | a′ | b′ | |
| y = a + b lnx | ln x | y | a′ | b′ | |
| y = a/(b + x) | x | 1/y | 1/ b′ | a′/ b′ | |
| y = ax/(b + x) | x | x/y | 1/ b′ | a′/ b′ | |
| y = aeb/x | 1/x | ln y | ea′ | b′ | |
| y = a10b/x | 1/x | lg y | 10a′ | b′ | |
| y = a + bxn | xn | y | a′ | b′ |
Варіанти завдань:
І. 3, 11; ІІ. 4, 9; ІІІ. 2, 10; ІV. 13, 15; V. 8, 12; VI. 5, 16; VII. 6, 12; VIII. 14, 4;
IX. 7, 11; X. 2, 15; XI. 3, 14; XII. 4, 16; XIII. 5, 13; XIV. 6, 9; XV. 7, 12;
XVI. 8, 2; XVII. 9, 10; XVIII. 10, 14; XIX. 11, 12; XX. 12, 16; XXI. 13, 16;
XXII. 14, 2; XXIII. 15, 9; XXIV 16, 6; XXV. 13, 6; XXVI. 4, 5.
Задача 2. Для експериментальних даних, приведених в першій задачі цього розділу, додатково прийняти до уваги дані про основні фонди підприємства та їх вплив на розвиток виробництва (x2) і виконати наступне:
а) взяти лінійну регресійну модель y(x1;x2) у вигляді:
y = b0 + b1x1 + b2x2,
і визначити числові значення b0, b1, b2;
б) проаналізувати, чому коефіцієнт впливу x1 на y (тобто b1) в першій і в другій задачах відрізняються. Пояснити це явище.
в)оцінити отриману модель, розрахувавши дисперсії, коефіцієнти кореляції та детермінації:
