Цель работы
Научиться шифровать данные, используя системы с общим ключом.
Краткие теоретические сведения
Двумя наиболее популярными алгоритмами криптографических схем с открытым ключом являются алгоритмы RSA и Деффи-Хеллмана.
Алгоритм RSA
Данный алгоритм был предложен в 1977 году. RSA представляет собой блочный шифр, в котором открытый и шифрованный текст представляют целыми числами из диапазона от 0 до n-1 для некоторого n. Шифрование и дешифрование для блока открытого текста M и блока шифрованного текста C можно представить в виде следующих формул: 
. Как отправитель, так и получатель должны знать значения n и e, но только получателю известно значение d. Т.е., данная схема является алгоритмом шифрования с открытым ключом KU={e, n} и личным ключом KR={d, n}. Для данного алгоритма должны выполнятся следующие условия.
1. Должны существовать такие значения e, d и n, при которых 
для всех M<n.
2. Должны относительно легко вычисляться 
и С для всех значений M<n.
3. Должно быть практически невозможно определить d по имеющимся e и n.
Алгоритм. Выбираются два простых ключа p и q, и вычисляется их произведение n, которое будет служить модулем сравнения при шифровании и дешифровании. Затем рассматривается величина 
, называемая функцией Эйлера, значение которой равно числу положительных целых чисел, не превышающих n и взаимно простых с n. После этого выбирается целое значение e, взаимно простое с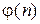 
(это значит, что наибольшим общим делителем этих чисел является 1). Затем вычисляется значение d, являющееся мультипликативным обратным значения e по модулю (
).
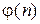Пример. Предположим, что пользователь A опубликовал свой открытый ключ, и теперь пользователь B собирается переслать ему сообщение M. Пользователь B вычисляет C и пересылает его. Получив шифрованный текст, пользователь A дешифрует его. Ключи вычисляются следующим образом.
1. Выбираются два простых числа, p=7 и q=17.
2. Вычисляется n=p*q=7*17=119.
3. Вычисляется 
.
4. Выбирается e, взаимно простое с 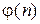и меньше, чем 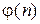; в данном случае e=5.
5. Определяется такое d, что d*e=1 mod 96 и d<96. Соответствующим значением будет d=77, так как 77*5=385=4*96+1.
В результате получают открытый ключ KU={5,119} и личный ключ KR={77,119}. Рассмотрим пример с вводимым текстом M=19. при шифровании 19 возводится в пятую степень, что в результате дает 2476099. В результате деления на 119 определяется остаток равный 66. Поэтому шифрованным текстом будет 66.
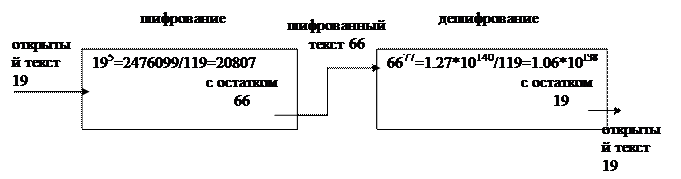
При дешифровании выясняется, что 
.
Рис. 6 Пример шифрования с использованием алгоритма RSA
Взлом алгоритма RSA можно осуществить перебором всех возможных вариантов ключей. Поэтому чем больше битов содержат e и d, тем более защищенным оказывается алгоритм. Однако вычисления, выполняемые и при генерировании ключа, и при шифровании/дешифровании, оказываются достаточно сложными, поэтому, чем больше длина ключа, тем медленнее будет работать система.
