Марковский процесс характеризуется дискретным временем и конечным множеством состояний. Временной параметр пробегает неотрицательные числовые значения, а процесс (цепочка) определяется набором вероятностей перехода 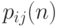 , т.е. вероятностью перейти на
, т.е. вероятностью перейти на  -шаге из состояния
-шаге из состояния  в состояние
в состояние  . Процесс называется однородным, если он не зависит от
. Процесс называется однородным, если он не зависит от  . В моделях, базирующихся на процессе Маркова, предполагается, что количество дефектов, обнаруженных в ПС, в любой момент времени зависит от поведения системы и представляется в виде стационарной цепи Маркова. При этом количество дефектов конечное, но является неизвестной величиной, которая задается для модели в виде константы. Интенсивность отказов в ПС или скорость прохода по цепи зависит лишь от количества дефектов, которые остались в ПС. К этой группе моделей относятся: Джелински- Моранды, Шика-Вулвертона, Шантикумера и др.
. В моделях, базирующихся на процессе Маркова, предполагается, что количество дефектов, обнаруженных в ПС, в любой момент времени зависит от поведения системы и представляется в виде стационарной цепи Маркова. При этом количество дефектов конечное, но является неизвестной величиной, которая задается для модели в виде константы. Интенсивность отказов в ПС или скорость прохода по цепи зависит лишь от количества дефектов, которые остались в ПС. К этой группе моделей относятся: Джелински- Моранды, Шика-Вулвертона, Шантикумера и др.
Ниже рассматриваются некоторые модели надежности, которые обеспечивают рост надежности ПО (модели роста надежности), находят широкое применение на этапе тестирования и описывают процесс обнаружения отказов при следующих предположениях:
все ошибки в ПС не зависят друг от друга с точки зрения локализации отказов;
интенсивность отказов пропорциональна текущему числу ошибок в ПС (убывает при тестировании программного обеспечения);
вероятность локализации отказов остается постоянной;
локализованные ошибки устраняются до того, как тестирование будет продолжено;
при устранении ошибок новые ошибки не вносятся.
Приведем основные обозначения величин при описании моделей роста надежности:
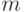 - число обнаруженных отказов ПО за время тестирования;
- число обнаруженных отказов ПО за время тестирования;
 - интервалы времени между отказами
- интервалы времени между отказами 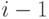 и
и  , при
, при  ;
;
 - моменты времени отказов (длительность тестирования до
- моменты времени отказов (длительность тестирования до  -отказа),
-отказа),  при
при 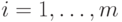 ;
;
 - продолжительность тестирования ПО (время, для которого определяется надежность);
- продолжительность тестирования ПО (время, для которого определяется надежность);
 - оценка числа ошибок в ПО в начале тестирования;
- оценка числа ошибок в ПО в начале тестирования;
 - оценка числа прогнозированных ошибок;
- оценка числа прогнозированных ошибок;
 - оценка среднего времени до следующего отказа;
- оценка среднего времени до следующего отказа;
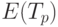 - оценка среднего времени до завершения тестирования;
- оценка среднего времени до завершения тестирования;
 - оценка дисперсии;
- оценка дисперсии;
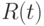 - функция надежности ПО;
- функция надежности ПО;
 - функция риска в момент времени
- функция риска в момент времени  между
между 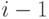 и
и  -отказами;
-отказами;
 - коэффициент пропорциональности;
- коэффициент пропорциональности;
 - частота обнаружения ошибок.
- частота обнаружения ошибок.
Далее рассматриваются несколько моделей роста надежности, основанные на этих предположениях и использовании результатов тестирования программ в части отказов, времени между ними и др.
Модель Джелинского-Моранды. В этой модели используются исходные данные, приведенные выше, а также:
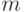 - число обнаруженных отказов за время тестирования;
- число обнаруженных отказов за время тестирования;
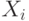 - интервалы времени между отказами;
- интервалы времени между отказами;
 - продолжительность тестирования.
- продолжительность тестирования.
Функция риска  в момент времени
в момент времени  расположена между
расположена между 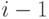 и
и  имеет вид:
имеет вид:

где 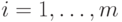 ;
; 
Эта функция считается ступенчатой кусочнопостоянной функцией с постоянным коэффициентом пропорциональности и величиной ступени -  . Оценка параметров
. Оценка параметров  и
и  производится с помощью системы уравнений:
производится с помощью системы уравнений:
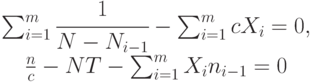
При этом суммарное время тестирования вычисляется так: 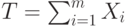
Выходные показатели для оценки надежности относительно указанного времени  включают:
включают:
число оставшихся ошибок 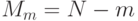 ;
;
среднее время до текущего отказа  ;
;
среднее время до завершения тестирования и его дисперсию

При этом функция надежности вычисляется по формуле:

при  и числе ошибок, найденных и исправленных на каждом интервале тестирования, равным единице.
и числе ошибок, найденных и исправленных на каждом интервале тестирования, равным единице.
Модель Шика-Вулвертона. Модель используется тогда, когда интенсивность отказов пропорциональна не только текущему числу ошибок, но и времени, прошедшему с момента последнего отказа. Исходные данные для этой модели аналогичны выше рассмотренной модели Джелински-Моранды:
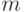 - число обнаруженных отказов за время тестирования,
- число обнаруженных отказов за время тестирования,
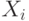 - интервалы времени между отказами,
- интервалы времени между отказами,
 - продолжительность тестирования.
- продолжительность тестирования.
Функции риска  в момент времени между
в момент времени между 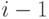 и
и 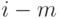 отказами определяются следующим образом:
отказами определяются следующим образом:

Эта функция является линейной внутри каждого интервала времени между отказами, возрастает с меньшим углом наклона. Оценка c и N вычисляется из системы уравнений:
К выходным показателям надежности относительно продолжительности  относятся:
относятся:
число оставшихся ошибок  ;
;
среднее время до следующего отказа MTт = (р / (2 (N - m) c))1/2;
среднее время до завершения тестирования и его дисперсия

Функция надежности вычисляется по формуле:
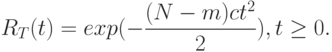
Модели пуассоновского типа базируются на выявлении отказов и моделируются неоднородным процессом, который задает  - неоднородный пуассоновский процесс с функцией интенсивности
- неоднородный пуассоновский процесс с функцией интенсивности  , что соответствует общему количеству отказов ПС за время его использования
, что соответствует общему количеству отказов ПС за время его использования  .
.
Модель Гоело-Окумото. В основе этой модели лежит описание процесса обнаружения ошибок с помощью неоднородного пуассоновского процесса, ее можно рассматривать как модель экспоненциального роста. В этой модели интенсивность отказов также зависит от времени. Кроме того, в ней количество выявленных ошибок трактуется как случайная величина, значение которой зависит от теста и других условных факторов.
Исходные данные этой модели:
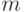 - число обнаруженных отказов за время тестирования;
- число обнаруженных отказов за время тестирования;
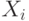 - интервалы времени между отказами;
- интервалы времени между отказами;
 - продолжительность тестирования.
- продолжительность тестирования.
Функция среднего числа отказов, обнаруженных к моменту  , имеет вид
, имеет вид

где  - интенсивность обнаружения отказов и показатель роста надежности
- интенсивность обнаружения отказов и показатель роста надежности  .
.
Функция интенсивности  в зависимости от времени работы до отказа равна
в зависимости от времени работы до отказа равна

Оценка  и
и  получаются из решения уравнений:
получаются из решения уравнений:
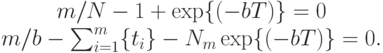
Выходные показатели надежности относительно времени  определяют:
определяют:
среднее число ошибок, которые были обнаружены в интервале  , по формуле
, по формуле  ,
,
функцию надежности
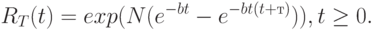
В этой модели обнаружение ошибки трактуется как случайная величина, значение которой зависит от теста и операционной среды.
В других моделях количество обнаруженных ошибок рассматривается как константа.В моделях роста надежности исходной информацией для расчета надежности являются интервалы времени между отказами тестируемой программы, число отказов и время, для которого определяется надежность программы при отказе. На основании этой информации по моделям определяются показатели надежности вида:
вероятность безотказной работы;
среднее время до следующего отказа;
число необнаруженных отказов (ошибок);
среднее время дополнительного тестирования программы.
Модель анализа результатов прогона тестов использует в своих расчетах общее число экспериментов тестирования и число отказов. Эта модель определяет только вероятность безотказной работы программы и выбрана для случаев, когда предыдущие модели нельзя использовать (мало данных, некорректность вычислений). Формула определения вероятности безотказной работы по числу проведенных экспериментов имеет вид
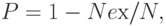
где  - число ошибочных экспериментов,
- число ошибочных экспериментов,  - число проведенных экспериментов для проверки работы ПС.
- число проведенных экспериментов для проверки работы ПС.
Таким образом, можно сделать вывод о том, что модели надежности ПС основаны на времени функционирования и/или количестве отказов (ошибок), полученных в программах в процессе их тестирования или эксплуатации. Модели надежности учитывают случайный марковский и пуассоновский характер соответственно процессов обнаружения ошибок в программах, а также характер и интенсивность отказов.
Контрольные вопросы и задания
1.Определите понятие качество ПО.
2.Назовите основные аспекты и уровни модели качества ПО.
3.Определите характеристики качества ПО и их назначение.
4.Какие методы используются при определении показателей качества?
5.Определите метрики программного продукта и их составляющие.
6.Какие стандарты в области качества ПО существуют?
7.Назовите основные цели и задачи системы управления качеством.
8.В чем суть инженерии качества? Назовите критерии классификации моделей надежности.
9.Дайте определение типов моделей надежности и их базис.
10.В чем отличие марковских и пуассоновских моделей надежности?
Список литературы.
1.ISO/IEC 9126. Infofmation Technology. – Software Quality Characteristics and metrics. –
1997.
2. ДСТУ 2844–1994. Программные средства ЭВМ. Обеспечение качества. Термины и
определения..
3. ДСТУ 2850–1994. Программные средства ЭВМ. Обеспечение качества. Показатели и
методы оценки качества программного обеспечения.
4. ДСТУ 3230–1995. Управление качества и обеспечение качества. Термины и
определения.
5. Кулаков А.Ю. Оценка качества программ ЭВМ.–Киев: Технiка.–1984.–167с.
6. Липаев В.В. Методы обеспечения качества крупномасштабных программных
систем. – М.: СИНТЕГ.– 2003.–510 с.
7. Андон Ф.И., Суслов В.Ю., Коваль Г.И., Коротун Т.М. Основы качества
программных систем.–Киев, Академпериодика.– 2002.–502с.
8. Липаев В.В. Надежность программного обеспечения АСУ.–М.: Сов.радио, 1977.–
400с.
9. Майерс Г. Надежность программного обеспечения.– М.: Мир, 1980.–360с.
10. Гласс Г. Руководство по надежному программированию.–М.: Финансы и
Статистика, 1982.–256с.
11. Тейер Т., Липов Р., Нельсон Э. Надежность программного обеспечения.–М.:
Мир, 1981.– 325с.
12. Мороз Г.Б., Лаврищева Е.М. Модели роста надежности программного
обеспечения.– Киев.–Препринт 92–38, 1992.– 23с.
13. Коваль Г.И. Подход к прогнозированию надежности ПО при управлении проектом
// Проблемы программирования. –2002. – № 1 – 2. – С. 282 – 290.
14.Goel A.L. Software reliability models& Assumptions, Limitations and Applicability//
IEEE Trans.– N2.–p.1411–1423.
15. Sukert A.N., Goel A.L. A guidebook for software reliability assessment /Proc. Annual
Reliability and Maintainability Symp. – Tokio (Japan). – 1980. –P. 186 – 190.






