Задача определения стандарта естественной рождаемости встала перед Э. Коулом в связи с реализацией в конце 1960-х гг. проекта исследования снижения рождаемости в Европе в XVIII-XX вв., известного под названием «Принстонское исследование европейской рождаемости»23. Э. Коул в то время был директором Центра демографических исследований Принстонского университета. В распоряжении исследователей были только данные переписей европейских стран о распределении населения по полу и возрасту и о ежегодных числах родившихся. Информация о рождениях извлекалась, главным образом, из приходских записей о регистрации крещений.
Такого рода данные позволяли рассчитывать только специальные коэффициенты рождаемости, но не ее суммарные коэффициенты, поскольку данные о распределении родившихся по возрасту матери отсутствовали. Но специальные коэффициенты рождаемости, как мы помним, не полностью свободны от влияния возрастной структуры. Пытаясь разрешить эту проблему. Э. Коул разработал три индекса рождаемости, известные ныне как индексы Коула24:
· индекс общей рождаемости (If);
· индекс брачной рождаемости (Ig);
· индекс внебрачной рождаемости (Ih).
Эти индексы измеряли реальную рождаемость в ее соотношении со стандартом естественной рождаемости. По своей природе эти индексы являются примером косвенной стандартизации показателей рождаемости. Они выражают тот уровень рождаемости (ее общего коэффициента), который бы наблюдался в реальном населении, если бы повозрастные ее показатели были бы такими, как в стандарте естественной рождаемости, в качестве какового, согласно Э. Коулу, следует брать рождаемость гуттеритов, репродуктивное поведение которых соответствует перечисленным выше критериям. Наивысшие показатели брачной рождаемости гуттеритов были зафиксированы в 1920- 1930 гг. (табл. 5.5).
Кроме того, им был предложен четвертый индекс - индекс брачной структуры (1т), который измеряет влияние на уровень рождаемости изменений брачной структуры населения.
Индекс общей рождаемости (If) равен отношению наблюдаемого числа рождений к ожидаемому при условии, что реальное население имеет те же повозрастные показатели, что и стандарт естественной рождаемости:
Таблица 5.5 Стандартные коэффициенты рождаемости, %о
| Возраст | Гуттериты | ГМЕР | Россия, 1998 |
| 15-19 | - | ||
| 20-24 | |||
| 25-29 | |||
| 30-34 | 33.4 | ||
| 35-39 | 11.5 | ||
| 40-44 | 2.3 | ||
| 45-49 | 0.1 |
Здесь В - годовое число рождений; ASFRX - наблюдаемые повозрастные коэффициенты рождаемости; Fx - среднегодовая численность женщин возраста x;ASFRs - повозрастные коэффициенты рождаемости стандарта (гуттеритов).
Индекс брачной рождаемости (Ig) равен отношению наблюдаемого числа рождений в браке к ожидаемому при условии, что реальное население имеет те же повозрастные показатели брачной рождаемости, что и стандарт естественной рождаемости:

где Bg - годовое наблюдаемое число брачных рождений (Bg = ASFRggFx); ASFRg - наблюдаемые повозрастные коэффициенты брачной рождаемости; gFx - численность женщин возраста х, состоящих в браке; ASFRS - повозрастные коэффициенты рождаемости стандарта (гуттеритов).
Индекс внебрачной рождаемости (Ih) равен отношению наблюдаемого числа рождений вне брака к ожидаемому при условии, что реальное население имеет повозрастные показатели внебрачной рождаемости, равные стандарту естественной рождаемости:

где Bh - годовое наблюдаемое число внебрачных рождений (Bh = ASFRh-hFx); ASFRh - наблюдаемые повозрастные коэффициенты внебрачной рождаемости; hFx - численность женщин возраста х, не состоящих в браке; ASFRs - повозрастные коэффициенты рождаемости стандарта (гуттеритов1
Индекс брачной структуры равен отношению ожидаемого числа брачных рождений к ожидаемому числу всех рождений:

Это выражение можно представить иначе
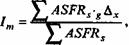
где gx - доля женщин возрастах, состоящих в браке, равная g Fx/Fx
Иначе говоря, индекс брачной структуры равен средневзвешенной доле женщин репродуктивного возраста, состоящих в браке, причем весами выступают повозрастные коэффициенты стандарта естественной рождаемости. Это позволяет легко рассчитывать индекс Im, зная лишь повозрастные доли замужних женщин.
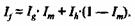
Если же внебрачная рождаемость отсутствует, т. е. Ih = 0, то это соотношение равно:
Поскольку Б = Bg + Bh и Fx = gFx + hFx, индексы рождаемости связаны между собой следующим соотношением:

В табл. 5.6 приведен пример расчета индексов Коула для населения России (1994 г.). Как видно из таблицы, население России использует максимальный потенциал рождаемости менее, чем на 10%.
Гипотетический минимум естественной рождаемости Российский демограф В.А. Борисов, разрабатывая свой вариант нормативного подхода, исходил из того, что использовать рождаемость гуттеритов в качестве стандарта естественной рождаемости методологически неправильно из-за уникальности этого субнаселения. По его мнению, таким стандартом может быть только стандарт, разработанный на основе математической модели репродуктивного процесса, так как только в этом случае можно «использовать массовые фактические данные». По мнению В.А. Борисова, более правильно определять не максимум, а минимум естественной рождаемости, чтобы быть уверенным, что уровень естественной брачной рождаемости не опустится ниже этого минимума в нормальных санитарных условиях. Поэтому в упомянутой математической модели надо брать такие значения ее параметров, которые находились бы в пределах санитарной нормы и были бы в ее пределах наименее благоприятными.
Таблица 5.6






