Основание восьмеричной системы счисления равно 8 (p=8) определяет число цифр входящих в данную систему счисления: {0,1,2,3,4,5,6,7} восемь цифр. Восьмеричная система счисления, так же как и десятичная является позиционной. Формула разложения по степени основания числа записанного в восьмеричной системе счисления имеет следующий вид:
где:
- значение числа в восьмеричной системе счисления;
q – количество разрядов числа записанного в восьмеричной системе счисления.
I – номер разряда;
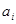- значение i-го разряда числа записанного в восьмеричной системе счисления.
Так для четырехразрядного числа, записанного в двоичной системе счисления формула разложения по степени основания будет иметь следующий вид:
Восьмеричная система счисления.
Основание шестнадцатеричной системы счисления равно 16 (p=16) определяет число цифр входящих в данную систему счисления: {0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F} шестнадцать цифр. Поскольку в алфавит шестнадцатеричной системы счисления входит больше дести цифр, определенных для десятичной системы счисления, остальные цифры обозначаются буквами латинского алфавита. Шестнадцатеричная система счисления, так же как и десятичная является позиционной. Формула разложения по степени основания числа записанного в шестнадцатеричной системе счисления имеет следующий вид:
где:
- значение числа в шестнадцатеричной системе счисления;
q – количество разрядов числа записанного в шестнадцатеричной системе счисления.
I – номер разряда;
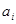- значение i-го разряда числа записанного в шестнадцатеричной системе счисления.
Так для четырехразрядного числа, записанного в шестнадцатеричной системе счисления формула разложения по степени основания будет иметь следующий вид:
Взаимосвязь систем счисления используемых в вычислительной технике.
Двоичная система счисления, используемая элементами вычислительной техники имеет один недостаток – это громоздкость записи. Для того, чтобы записать число 255(10) требуется целых восемь разрядов 11111111(2). Для уменьшения разрядности при записи информации требовалось разработать системы счисления, в которые было бы легко переводить информацию из двоичной системы счисления, и при этом запись была бы менее громоздкой. Сначала была разработана восьмеричная система счисления, в которой тоже самое число 255(10) представлялось в виде 377(8), а затем шестнадцатеричная, это же число в которой имеет вид FF(16). Перевод между этими системами счисления можно осуществлять при помощи таблицы 2.
Таблица 2.
| Двоичная | Восьмеричная | Шестнадцатеричная |
| A | ||
| B | ||
| C | ||
| D | ||
| E | ||
| F |
