Вычисление квадратного корня производится путем деления исходного числа на переменный делитель [14]. Первое значение переменного делителя равно 0,01, следующие значения формируются путем приписывания пары цифр 01 к уже найденному числу.
Для нахождения результата нужно выполнить (n-2) цикла, каждый из которых может содержать три такта:
1) из значения на сумматоре вычитается содержимое переменного делителя (РгД) и определяется очередная цифра результата, которая равна инверсии знака сумматора;
2) если после выполнения вычитания сумматор меньше нуля, то нужно выполнить восстановление сумматора путем сложения его с содержимым переменного делителя;
3) производится сдвиг содержимого сумматора на один разряд влево и формируется новый переменный делитель.
Нужно помнить, что из отрицательных чисел корень не вычисляется.
Схема алгоритма извлечения квадратного корня в соответствии с описанным алгоритмом изображена на рис. 4.7.
 |
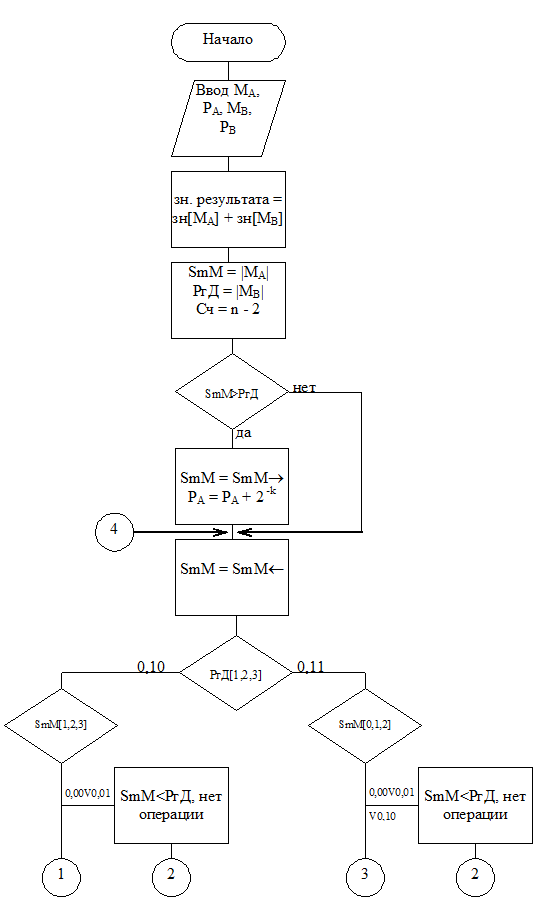Рис. 4.6. Схема алгоритма ускоренного деления
с анализом двух разрядов делителя
Рис. 4.6. Схема алгоритма ускоренного деления с анализом двух разрядов делителя (окончание)
 |
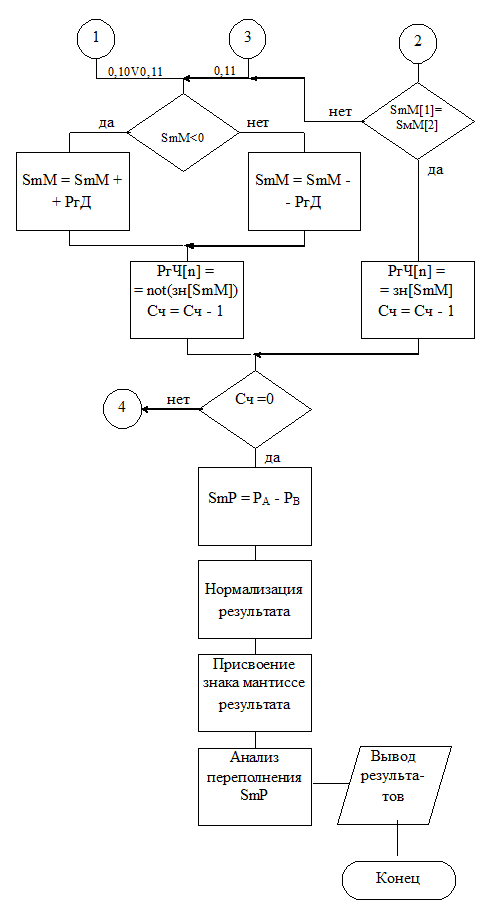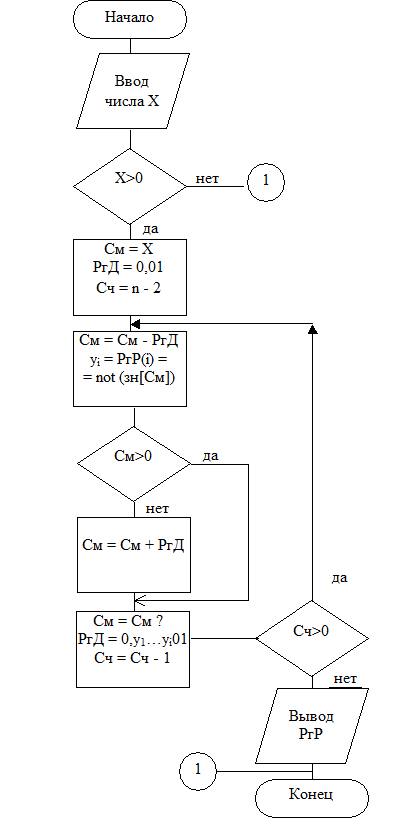
Рис. 4.7. Схема алгоритма вычисления квадратного корня
Буквами yi обозначены разряды регистра результата (РгР). Начальное значение счетчика во всех алгоритмах принимается равным (n-2), где n – число разрядов исходных чисел, так как используются модифицированные коды.
Рассмотрим пример для операции вычисления квадратного корня для числа с фиксированной запятой. Извлечем квадратный корень из числа А = 0,101111 по разработанному алгоритму.
См = 0,101111 РгР = 0 (регистр результата)
+ 1,110000 РгД = 0,01 (переменный делитель)
I 1) См= См-РгД = 0,011111 РгР = 0,1 (так как См>0)
3) См = См← = 0,111110 РгД = 0,101
+ 1,011000
II 1) См= См-РгД = 0,010110 РгР = 0,11 (См>0)
3) См = См← = 0,101100 РгД = 0,1101
+ 1,001100
III 1) См= См-РгД = 1,111000 РгР = 0,110 (так как См<0)
+ 0,110100
2) См=См+РгД = 0,101100
3) См = См← = 1,011000 РгД = 0,11001
+ 1,001110
IV 1) См= См-РгД = 0,100110 РгР = 0,1101 (так как См>0)
3) См = См← = 1,001100 РгД = 0,110101
+ 1,001011
V 1) См= См-РгД = 0,010111 РгР = 0,11011 (так как См>0)
3) См = См← = 0,101110 РгД = 0,1101101
+ 1,0010011
VI 1) См= См-РгД = 0,010111 РгР = 0,110110 (так как См<0)
В циклах I, II, IV и V пропущен второй такт, потому что сумматор положителен и восстановление остатка не требуется.
Ответ: В =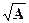 
= 0,110110, что соответствует результату, полученному при извлечении корня из числа А программой «Операции».
В настоящей главе проанализирована часть алгоритмов реализации программных моделей операций, изучаемых в курсе «Дискретная математика». Приведены схемы алгоритмов перевода чисел из одной позиционной системы счисления в другую, а также для выполнения арифметических операций сложения (вычитания), умножения, деления и вычисления квадратного корня для двоичных чисел, в том числе и ускоренные методы умножения и деления. Таким же образом можно проектировать любые алгоритмы выполнения операций, описанных в теоретических главах 2 и 3.
МАТЕМАТИЧЕСКАЯ ЛОГИКА
