Упорядкування структур даних

Кодування текстових даних

Якщо кожному символу алфавіту зіставити визначене ціле число (наприклад, порядковий номер), то за допомогою двійкового коду можна кодувати і текстову інформацію. Восьми двійкових розрядів досить для кодування 256 різних символів. Цього вистачить, щоб виразити різними комбінаціями восьми бітів усі символи англійської і російської мов, як рядкові, так і прописні, а також розділові знаки, символи основних арифметичних дій і деякі загальноприйняті спеціальні символи, наприклад символ «§».

Технічно це виглядає дуже просто, однак завжди існували досить вагомі організаційні складності. У перші роки розвитку обчислювальної техніки вони були пов'язані з відсутністю необхідних стандартів, а в даний час викликані, навпаки, великою кількістю одночасно діючих і суперечливих стандартів. Для того щоб весь світ однаково кодував текстові дані, потрібні єдині таблиці кодування, а це, поки що, неможливо через протиріччя між символами національних алфавітів, а також протиріч корпоративного характеру.

Для англійської мови, що захопила де-факто нішу міжнародного засобу спілкування, протиріччя вже зняті. Інститут стандартизації США (ANSI — American National Standard Institute) ввів у дію систему кодування ASCII (American Standard Code for Information Interchange — стандартний код інформаційного обміну США). У системі ASCII закріплені дві таблиці кодування — базова і розширена. Базова таблиця закріплює значення кодів від 0 до 127, а розширена відноситься до символів з номерами від 128 до 255.

Перші 32 коди базової таблиці, починаючи з нульового, віддані виробникам апаратних засобів (у першу чергу виробникам комп'ютерів і друкувальних пристроїв). У цій області розміщаються так звані керуючі коди, яким не відповідають ніякі символи мов, і, відповідно, ці коди не виводяться ні на екран, ні на пристрої друку, але ними можна керувати тим, як здійснюється виведення інших даних.

Починаючи з коду 32 по код 127 розміщені коди символів англійського алфавіту, розділових знаків, цифр, арифметичних дій і деяких допоміжних символів.

Аналогічні системи кодування текстових даних були розроблені і в інших країнах. Так, наприклад, у СРСР у цій області діяла система кодування КОИ-7 (код обміну інформацією, семизначний). Однак підтримка виробників устаткування і програм вивела американський код ASCII на рівень міжнародного стандарту, і національним системам кодування довелося «відступити» у другу, розширену частину системи кодування, що визначають значення кодів з 128 по 255. Відсутність єдиного стандарту в цій області призвело до великої кількості одночасно діючих кодувань. Тільки в Росії можна вказати три діючих стандарти кодування і ще два застарілих.

Так, наприклад, кодування символів російської мови, відоме як кодування Windows-1251, була введена «ззовні» — компанією Microsoft, але, з огляду на широке поширення операційних систем і інших продуктів цієї компанії в Росії, вона глибоко закріпилася. Це кодування використовується на більшості локальних комп'ютерів, що працюють на платформі Windows.

Інше розповсюджене кодування зветься КОИ-8 (код обміну информацією, восьмизначний) — її походження відноситься до часів дії Ради Економічної Взаємодопомоги держав Східної Європи. Сьогодні кодування КОИ-8 широко використовується в комп'ютерних мережах на території Росії й у російському секторі Інтернету.

Міжнародний стандарт, у якому передбачене кодування символів російського алфавіту, зветься кодування ISO (International Standard Organization — Міжнародний інститут стандартизації). На практиці дане кодування використовується рідко.

На комп'ютерах, що працюють в операційних системах MS-DOS, можуть діяти ще два кодування (кодування ГОСТ і кодування ГОСТ-альтернативна). Перша з їх вважалася застарілою навіть у перші роки появи персональної обчислювальної техніки, але друга використовується і донині.

У зв'язку з великою кількістю систем кодування текстових даних, що діють у Росії, виникає задача міжсистемного перетворення даних — це одна з розповсюджених задач інформатики.

Універсальна система кодування текстових даних

Якщо проаналізувати організаційні труднощі, пов'язані зі створенням єдиної системи кодування текстових даних, то можна прийти до висновку, що вони викликані обмеженим набором кодів (256). В той же час очевидно, що якщо, наприклад, кодувати символи не восьмирозрядними двійковими числами, а числами з великою кількістю розрядів, то і діапазон можливих значень кодів стане набагато більшим. Така система, заснована на 16-розрядному кодуванні символів, одержала назву універсальної — UNICODE. Шістнадцять розрядів дозволяють забезпечити унікальні коди для 65 536 різних символів — цього діапазону досить для розміщення в одній таблиці символів більшості мов планети.

Незважаючи на тривіальну очевидність такого підходу, простий механічний перехід на дану систему довгий час стримувався через недостатні ресурси засобів обчислювальної техніки (у системі кодування UNICODE усі текстові документи автоматично стають удвічі довші). У другій половині 90-х років технічні засоби досягли необхідного рівня забезпеченості ресурсами, і сьогодні ми спостерігаємо поступовий переклад документів і програмних засобів на універсальну систему кодування. Для індивідуальних користувачів це ще більше додало турбот із узгодженням документів, виконаних у різних системах кодування із програмними засобами, але це треба розуміти як труднощі перехідного періоду.

2.6. Кодування графічних даних

Якщо розглянути за допомогою збільшувального скла чорно-біле графічне зображення, надруковане в газеті чи книзі, то можна побачити, що воно складається з дрібних крапок, що утворюють характерний візерунок, що називають растром.

Оскільки лінійні координати й індивідуальні властивості кожної крапки (яскравість) можна виразити за допомогою цілих чисел, то можна сказати, що растрове кодування дозволяє використовувати двійковий код для представлення графічних даний. Загальноприйнятим на сьогоднішній день вважається представлення чорно-білих ілюстрацій у вигляді комбінації крапок з 256 градаціями сірого кольору, і, таким чином, для кодування яскравості будь-якої крапки звичайно досить восьмирозрядного двійкового числа.

Для кодування кольорових графічних зображень застосовується принцип декомпозиції довільного кольору на основні складові. У якості таких складових використовують три основні кольори: червоний (Red, R), зелений (Green, G) і синій (Blue, В). На практиці вважається (хоча теоретично це не зовсім так), що будь-який колір, видимий людським оком, можна одержати шляхом механічного змішування цих трьох основних кольорів. Така система кодування називається системою RGB по перших буквах назв основних кольорів.

Якщо для кодування яскравості кожної з основних складових використовувати по 256 значень (вісім двійкових розрядів), як це прийнято для напівтонових чорно-білих зображень, то на кодування кольору однієї крапки треба затратити 24 розряди. При цьому система кодування забезпечує однозначне визначення 16,5 млн. різних кольорів, що насправді близько до чутливості людського ока. Режим представлення кольорової графіки з використанням 24 двійкових розрядів називається повнокольоровим (True Color).

Кожному з основних кольорів можна поставити у відповідність додатковий колір, тобто колір, що доповнює основний колір до білого. Неважко помітити, що для кожного з основних кольорів додатковим буде колір, утворений сумою пари інших основних кольорів. Відповідно, додатковими кольорами є: блакитний (Cyan,С), пурпурний (Magenta, M) і жовтий (Yellow, Y). Принцип декомпозиції довільного кольору на складові компоненти можна застосовувати не тільки для основних кольорів, але і для додаткових, тобто будь-який колір можна представити у вигляді суми блакитної, пурпурної і жовтої складової. Такий метод кодування кольору прийнятий у поліграфії, але в поліграфії використовується ще і четверта фарба — чорна (Black, К). Тому дана система кодування позначається чотирма буквами CMYK (чорний колір позначається буквою К, тому, що буква В вже зайнята синім кольором), і для представлення кольорової графіки в цій системі треба мати 32-бітний двійковий розряд. Такий режим теж називається повнокольоровим (True Color).

Якщо зменшити кількість двійкових розрядів, що використовуються для кодування кольору кожної крапки, то можна скоротити обсяг даних, але при цьому діапазон кольорів, що кодуються, помітно скорочується. Кодування кольорової графіки 16-розрядними двійковими числами називається режимом High Color.

При кодуванні інформації про колір за допомогою восьми біт дані можна передати тільки 256 колірними відтінками. Такий метод кодування кольору називається індексним. Зміст назви в тім, що, оскільки 256 значень зовсім недостатньо, щоб передати весь діапазон кольорів, доступний людському оку, код кожної крапки растру виражає не колір сам по собі, а тільки його номер (індекс) у деякій довідковій таблиці, що назвають палітрою. Зрозуміло, ця палітра повинна прикладатися до графічних даних — без неї не можна скористатися методами відтворення інформації на екрані чи папері (тобто, скористатися, звичайно, можна, але через неповноту даних отримана інформація не буде адекватною: листя на деревах може виявитися червоним, а небо — зеленим).

2.7. Кодування звукової інформації

Прийоми і методи роботи зі звуковою інформацією прийшли в обчислювальну техніку найпізніше. До того ж, на відміну від числових, текстових і графічних даних, у звукозаписів не було настільки ж тривалої і перевіреної історії кодування. У результаті методи кодування звукової інформації двійковим кодом далекі від стандартизації. Безліч окремих компаній розробили свої корпоративні стандарти, але якщо говорити узагальнено, то можна виділити два основних напрямки.

Метод FM (Frequency Modulation) заснований на тому, що теоретично будь-який складний звук можна розкласти на послідовність найпростіших гармонічних сигналів різних частот, кожний з яких являє собою правильну синусоїду, а отже, може бути описаний числовими параметрами, тобто кодом. У природі звукові сигнали мають безперервний спектр, тобто є аналоговими. Їхнє розкладання в гармонічні ряди і представлення у виді дискретних цифрових сигналів виконують спеціальні пристрої — аналогово-цифрові перетворювачі (АЦП). Зворотнє перетворення для відтворення звуку, закодованого числовим кодом, виконують цифро-аналогові перетворювачі (ЦАП). При таких перетвореннях неминучі втрати інформації, зв'язані з методом кодування, тому якість звукозапису звичайно виходить не цілком задовільною і відповідає якості звучання найпростіших электромузичних інструментів з оформленням, характерним для електронної музики. У той же час даний метод кодування забезпечує дуже компактний код, і тому він знайшов застосування ще в ті роки, коли ресурси засобів обчислювальної техніки були явно недостатні.

Метод таблично-хвильового (Wave-Table) синтезу краще відповідає сучасному рівню розвитку техніки. Якщо говорити спрощено, то можна сказати, що десь у заздалегідь підготовлених таблицях зберігаються зразки звуків для безлічі різних музичних інструментів (хоча не тільки для них). У техніці такі зразки називають семплами. Числові коди виражають тип інструмента, номер його моделі, висоту тону, тривалість і інтенсивність звуку, динаміку його зміни, деякі параметри середовища, у якому відбувається звучання, а також інші параметри, що характеризують особливість звуку. Оскільки як зразки використовуються «реальні» звуки, то якість звуку, отриманого в результаті синтезу, виходить дуже високою і наближається до якості звучання реальних музичних інструментів.

2.8.Основні структури даних

Робота з великими наборами даних автоматизується простіше, коли дані упорядковані, тобто утворюють задану структуру. Існує три основних типові структури даних: лінійна, ієрархічна і таблична. Їх можна розглянути на прикладі звичайної книги.

Якщо розібрати книгу на окремі аркуші і перемішати їх, книга втратить своє призначення. Вона як і раніше буде представляти набір даних, але підібрати адекватний метод для одержання з неї інформації дуже непросто. (Ще гірший вигляд справа буде мати, якщо з книги вирізувати кожну букву окремо — у цьому випадку навряд чи взагалі знайдеться адекватний метод для її прочитання.)

Якщо ж зібрати всі аркуші книги в правильній послідовності, ми одержимо найпростішу структуру даних — лінійну. Таку книгу вже можна читати, хоча для пошуку потрібних даних її прийдеться прочитати підряд, починаючи із самого початку, що не завжди зручно.

Для швидкого пошуку даних існує ієрархічна структура. Так, наприклад, книги розбивають на частини, розділи, глави, параграфи і т.п. Елементи структури більш низького рівня входять в елементи структури більш високого рівня: розділи складаються з глав, глави з параграфів і т.д.

Для великих масивів пошук даних в ієрархічній структурі набагато простіший, ніж у лінійній, однак і тут необхідна навігація, пов'язана з необхідністю перегляду. На практиці задачу спрощують тим, що в більшості книг є допоміжна перехресна таблиця, що зв'язує елементи ієрархічної структури з елементами лінійної структури, тобто єднає розділи, глави і параграфи з номерами сторінок. У книгах із простою ієрархічною структурою, розрахованих на послідовне читання, цю таблицю прийнято називати переліком заголовків, а в книгах зі складною структурою, що допускає вибіркове читання, її називають змістом.

Лінійні структури (списки даних, вектори даних)

Лінійні структури — це добре знайомі нам списки. Список — це найпростіша структура даних, що характеризується тим, що кожен елемент даних однозначно визначається своїм номером у масиві. Проставляючи номера на окремих сторінках розсипаної книги, ми створюємо структуру списку. Звичайний журнал відвідування занять, наприклад, має структуру списку, оскільки всі студенти групи зареєстровані в ньому під своїми унікальними номерами. Ми називаємо номери унікальними тому, що в одній групі не можуть бути зареєстровані два студенти з тим самим номером.

При створенні будь-якої структури даних треба вирішити два питання: як розділяти елементи даних між собою і як шукати потрібні елементи. У журналі відвідування, наприклад, це вирішується так: кожен новий елемент списку заноситься з нового рядка, тобто розділовим знаком є кінець рядка. Тоді потрібний елемент можна розшукати по номеру рядка.

N п/п Прізвище, Ім'я, По батькові

1 Лелека Олександр Олексійович

2 Бобров Борис Борисович

3 Воробйова Валентина Владиславівна

….. ………………………………………………

27 Сорокін Сергій Семенович

Розділовим знаком може бути і який-небудь спеціальний символ. Нам добре відомі розділові знаки між словами — це пропуски. У російській і в багатьох європейських мовах загальноприйнятим розділовим знаком є крапка. У розглянутому нами класному журналі як розділовий знак можна використовувати будь-який символ, що не зустрічається в самих даних, наприклад символ «*». Тоді наш список виглядав би так:

Лелека Олександр Олексійович * Бобров Борис Борисович * Воробйова Валентина Владиславівна *...* Сорокін Сергій Семенович.

У цьому випадку для пошуку елемента з номером п треба переглянути список, починаючи із самого початку і перерахувати розділові знаки, що зустрілися. Коли буде відлічене п-1 розділових знаків, розпочнеться потрібний елемент. Він закінчиться, коли буде зустрітий наступний розділовий знак.

Ще простіше можна діяти, якщо всі елементи списку мають рівну довжину. У цьому випадку розділові знаки в списку взагалі не потрібні. Для розшуку елемента з номером п треба переглянути список із самого початку і відрахувати а(п- 1) символ, де а — довжина одного елемента. З наступного символу почнеться потрібний елемент. Його довжина теж дорівнює а, тому його кінець визначити неважко. Такі спрощені списки, що складаються з елементів рівної довжини, називають векторами даних. Працювати з ними особливо зручно. Таким чином, лінійні структури даних (списки) — це упорядковані структури, у яких адреса елемента однозначно визначається його номером.

Табличні структури (таблиці даних, матриці даних)

З таблицями даних ми теж добре знайомі, досить згадати усім відому таблицю множення. Табличні структури відрізняються від лінійних тим, що елементи даних визначаються адресою комірки, що складається не з одного параметра, як у списках, а з декількох. Для таблиці множення, наприклад, адреси комірки визначаються номерами рядка і стовпця. Потрібний комірка знаходиться на їхньому перетині, а елемент зчитується з комірки.

При збереженні табличних даних кількість розділових знаків повинна бути більшою, ніж для даних, що мають структуру списку. Наприклад, коли таблиці друкують у книгах, рядки і стовпці розділяють графічними елементами — лініями вертикальної і горизонтальної розмітки (мал. 1.4).

Планета	Відстань до Сонця	Відносна маса	Кількість супутників
Меркурій	0,39	0,056
Венера	0,67	0,88
Земля	1,0	1,0
Марс	1,51	0,1
Юпітер	5,2

Якщо потрібно зберегти таблицю у виді довгого символьного рядка, використовують один розділовий знак - символ-роздільник між елементами, що належить одному рядку, і інший роздільник для відділення рядків, наприклад так:

Меркурій*0,39*0,056*0#Венера*0,67*0,88*0#Земля*1,0*1,0*1#Марс*1,51*0,1*2#…

Для пошуку елемента, що має адресу комірки (т, п), треба переглянути набір даних із самого початку і перерахувати зовнішні роздільники. Коли буде відлічений т-1 роздільник, треба перераховувати внутрішні роздільники. Після того як буде знайдений n-1 роздільник, знайдемо потрібний елемент. Він закінчиться, коли буде зустрінутий будь-який черговий роздільник.

Ще простіше можна діяти, якщо всі елементи таблиці мають рівну довжину. Такі таблиці називають матрицями. У даному випадку роздільники не потрібні, оскільки всі елементи мають рівну довжину і їх кількість відома. Для розшуку елемента з адресою (т, п) у матриці, що має М рядків і N стовпців, треба переглянути її із самого початку і відрахувати a [N(m -1) + (п -1)] символ, де а — довжина одного елемента. З наступного символу почнеться потрібний елемент. Його довжина теж дорівнює а, тому його кінець визначити неважко. Таким чином, табличні структури даних (матриці) — це упорядковані структури, у яких адреса елемента визначається номером рядка і номером стовпця, на перетині яких знаходиться комірка, що містить потрібний елемент.

Багатомірні таблиці. Вище ми розглянули приклад таблиці, що має два виміри (рядок і стовпець), але в житті нерідко приходиться мати справу з таблицями, у яких кількість вимірів більша. От приклад таблиці, за допомогою якої може бути організований облік студентів.

Номер факультету: 3

Номер курсу (на факультеті): 2

Номер спеціальності (на курсі): 2

Номер групи на потоці однієї спеціальності: 1

Номер студента в групі:19

Розмірність такої таблиці дорівнює п'яти, і для однозначного пошуку даних про учня в подібній структурі треба знати всі п'ять параметрів (координат).

Ієрархічні структури даних

Нерегулярні дані, які важко представити у вигляді списку чи таблиці, часто представляють у вигляді ієрархічних структур. З подібними структурами ми дуже добре знайомі по повсякденному життю. Ієрархічну структуру має система поштових адрес. Подібні структури також широко застосовуються у наукових систематизаціях і всіляких класифікаціях (мал. 1.5).

 

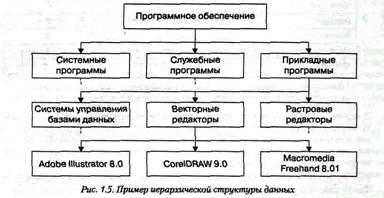
В ієрархічній структурі адреса кожного елемента визначається шляхом доступу (маршрутом), що веде від вершини структури до даного елемента. От, наприклад, як виглядає шлях доступу до команди, що запускає програму Калькулятор (стандартна програма комп'ютерів, що працює в операційній системі Windows 98):

Пуск > Программы > Стандартные > Калькулятор.

Дихотомія даних. Основним недоліком ієрархічних структур даних є збільшений розмір шляху доступу. Дуже часто буває так, що довжина маршруту виявляється більшою, ніж довжина самих даних, до яких він веде. Тому в інформатиці застосовують методи для регуляризації ієрархічних структур для того, щоб зробити шлях доступу компактним. Один з методів одержав назву дихотомії. Його суть зрозуміла з прикладу, представленого на мал. 1.6.

 

В ієрархічній структурі, побудованій методом дихотомії, шлях доступу до будь-якого елемента можна представити як шлях через раціональний лабіринт із поворотами ліворуч (0) чи праворуч (1) і, таким чином, виразити шлях доступу у вигляді компактного двійкового запису. У нашому прикладі шлях доступу до текстового процесора Word 2000 виразиться наступним двійковим числом: 1010.

Упорядкування структур даних

Лінійні й табличні структури є простими. Ними легко користуватися, оскільки адреса кожного елемента задається числом (для списку), двома числами (для двовимірної таблиці) чи декількома числами для багатомірної таблиці. Вони також легко упорядковуються. Основним методом упорядкування є сортування. Дані можна сортувати по будь-якому обраному критерію, наприклад: за алфавітом, по зростанню порядкового номера чи по зростанню якого-небудь параметра.

Незважаючи на численні зручності, у простих структур даних є і недолік — їх важко обновляти. Якщо, наприклад, перевести студента з однієї групи в іншу, зміни треба вносити відразу в два журнали відвідування; при цьому в обох журналах буде порушена облікова структура. Якщо переведеного студента вписати в кінець списку групи, порушиться упорядкування за алфавітом, а якщо його вписати відповідно до алфавіту, то зміняться порядкові номери всіх студентів, що розміщені за ним. Таким чином, при додаванні довільного елемента в упорядковану структуру списку може відбуватися зміна адресних даних у інших елементів.

У журналахуспішності це виправити неважко, але в системах, що виконують автоматичну обробку даних, потрібні спеціальні методи для вирішення цієї проблеми.

Ієрархічні структури даних за формою складніші, ніж лінійні і табличні, але вони не створюють проблем з відновленням даних. Їх легко розвивати шляхом створення нових рівнів. Навіть якщо в навчальному закладі буде створений новий факультет, це ніяк не відіб'ється на шляху доступу до інформації про інших студентів, що навчаються на факультеті.

Недоліком ієрархічних структур є відносна трудомісткість запису адреси елемента даних і складність упорядкування. Часто методи упорядкування в таких структурах засновують на попередній індексації, що полягає в тому, що кожному елементу даних привласнюється свій унікальний індекс, який можна використовувати при пошуку, сортуванні і т.п. Раніше розглянутий принцип дихотомії насправді є одним з методів індексації даних в ієрархічних структурах. Після такої індексації дані легко знаходяться по двійковому коду, зв'язаного з ними по індексу.

Адресні дані. Якщо дані зберігаються не хаотично, а в організованій структурі, то кожен елемент даних здобуває нову властивість (параметр), який можна назвати адресою. Звичайно, працювати з упорядкованими даними зручніше, але за це необхідно платити їх розмноженням, оскільки адреси елементів даних — це теж дані, і їх теж треба зберігати й обробляти.

3. Файли і файлова структура

3.1. Одиниці представлення даних

Існує безліч систем представлення даних. З однією з них, прийнятою в інформатиці й обчислювальній техніці, двійковим кодом, ми познайомилися вище. Найменшою одиницею такого представлення є біт (двійковий розряд).

Сукупність двійкових розрядів, що виражають числові чи інші дані, утворюють деякий бітовий малюнок. Практика показує, що з бітовим представленням зручніше працювати, якщо цей малюнок має регулярну форму. У даний час, як таку форму використовують групи з восьми бітів, що називаються байтами.

Десяткове число	Двійкове число	Байт
...	...	...

Поняття про байт, як групу взаємопов’язаних бітів, з'явилося разом з першими зразками електронної обчислювальної техніки. Довгий час воно було машинно-залежним, тобто для різних обчислювальних машин довжина байта була різною. Тільки наприкінці 60-х років поняття байта стало універсальним і машинно-незалежним.

В багатьох випадках доцільно використовувати не восьмирозрядне кодування, а 16-розрядне, 24-розрядне, 32-розрядне і більше. Група з 16 взаємозалежних біт (двох взаємозалежних байтів) в інформатиці називається словом. Відповідно, групи з чотирьох взаємозалежних байтів (32 розряду) називаються подвоєним словом, а групи з восьми байтів (64 розряду) — учетвереним словом. Поки що на сьогоднішній день такої системи позначення досить.

3.2. Одиниці виміру даних

Існує багато різних систем і одиниць виміру даних. Кожна наукова дисципліна і кожна область людської діяльності може використовувати свої, найбільш зручні чи традиційно вистояні одиниці. В інформатиці для виміру даних використовують той факт, що різні типи даних мають універсальне двійкове представлення, і тому вводять свої одиниці даних, засновані на цьому.

Найменшою одиницею виміру є байт. Оскільки одним байтом, як правило, кодується один символ текстової інформації, то для текстових документів розмір у байтах відповідає лексичному обсягу в символах (поки що виключення представляє розглянуте вище універсальне кодування UNICODE).

Більш велика одиниця виміру — кілобайт (Кбайт). Умовно можна вважати, що 1 Кбайт приблизно дорівнює 1000 байт. Умовність пов'язана з тим, що для обчислювальної техніки, що працює з двійковими числами, більш зручне представлення чисел у вигляді ступеня двійки, і тому насправді 1 Кбайт дорівнює 2¹⁰ байт (1024 байт). Однак усюди, де це не принципово, з інженерною погрішністю (до 3 %) «забувають» про «зайві» байти.

У кілобайтах вимірюють порівняно невеликі обсяги даних. Умовно можна вважати, що одна сторінка неформатованого машинописного тексту складає близько 2 Кбайт.

Більш великі одиниці виміру даних утворяться додаванням префіксів мега-, гига-, тера-; у більш великих одиницях поки що немає практичної потреби.

1 Мбайт = 1024 Кбайт = 2²⁰ байт

1 Гбайт = 1024 Мбайт = 2³⁰ байт

1 Тбайт = 1024 Гбайт = 2⁴⁰ байт

Особливо звернемо увагу на те, що при переході до більш великих одиниць «інженерна» погрішність, зв'язана з округленням, накопичується і стає неприпустимою, тому на старших одиницях виміру округлення роблять рідше.

3.3. Одиниці збереження даних

При збереженні даних зважуються дві проблеми: як зберегти дані в найбільш компактному виді і як забезпечити до них зручний і швидкий доступ (якщо доступ не забезпечений, то це не збереження). Для забезпечення доступу необхідно, щоб дані мали упорядковану структуру, а при цьому, як ми вже знаємо, утвориться «паразитне навантаження» у вигляді адресних даних. Без них не можна одержати доступ до потрібних елементів даних, що входять у структуру.

Оскільки адресні дані теж мають розмір і теж підлягають збереженню, зберігати дані у виді дрібних одиниць, таких, як байти, незручно. Їх незручно зберігати у більш великих одиницях (кілобайтах, мегабайтах і т.п.), оскільки неповне заповнення однієї одиниці збереження призводить до неефективності збереження.

За одиницю збереження даних прийнятий об'єкт змінної довжини, названий файлом. Файл — це послідовність довільного числа байтів, що має унікальне власниме ім'я. Звичайно в окремому файлі зберігають дані, що відносяться до одного типу. У цьому випадку тип даних визначає тип файлу.

Найпростіше представити собі файл у вигляді безрозмірного канцелярського досьє, у яке можна за бажанням додавати чи вилучати його зміст. Оскільки у визначенні файлу немає обмежень за розміром, можна уявити собі файл, що має 0 байтів (порожній файл), і файл, що має будь-яке число байтів.

У визначенні файлу особлива увага приділяється імені. Воно фактично несе в собі адресні дані, без яких дані, що зберігаються у файлі, не стануть інформацією через відсутність методу доступу до них. Крім функцій, пов'язаних з адресацією, ім'я файлу може зберігати і відомості про тип даних, які містяться у ньому. Для автоматичних засобів роботи з даними це важливо, оскільки по імені файлу вони можуть автоматично визначити адекватний метод вилучення інформації з файлу.