Выше мы обсудили несколько классических математических моделей в экологии. Известно и немало других, которые можно найти в книгах и в статьях научно-популярных журналов.
Использование математических моделей, основанных на дифференциальных уравнениях или их дискретных аналогах, далеко не единственный путь в компьютерном моделировании динамики популяций. Другую интересную группу составляют чисто стохастические модели или динамические модели с элементами стохастичности.Опишем две возможные модели такого класса: одну - без подробностей, которые рекомендуем продумать самостоятельно, другую -во всех деталях, включая реализующую ее программу.
Первая модель. Две популяции находятся в соотношении «хищник - жертва», описанном выше, но модель совершенно иная. На некотором клетчатом поле (которое наглядно - все или по частям - изображается на дисплее) находятся волки (несколько) и зайцы (много). Зайцы совершают беспорядочные перемещения, длины и направления которых - случайные величины, подчиняющиеся некоторому закону распределения вероятностей, а каждый волк в каждое мгновение ориентируется на ближайшего зайца и может совершать ограниченные прыжки. Если волк в течение некоторого, заранее определенного, промежутка времени остается без добычи (т.е. не попадает в клетку, где находится заяц), то он погибает. Зайцы и волки через определенные моменты размножаются, например, каждый второй заяц приносит двух потомков, каждый второй волк приносит одного потомка, причем скорость размножения волков в два раза ниже, чем зайцев. Все это может красочно изображаться на экране, состояние которого меняется через фиксированные моменты времени.
Это - чисто имитационное моделирование, конечной целью которого является, как и в описанных моделях, установление судьбы популяций в зависимости от многих факторов, входящих в модель. Здесь нет дифференциальных уравнений, но зато в полной мере проявляется стохастика, моделирование случайных процессов. Реализация такой модели требует большого программистского искусства, способствует формированию вероятностных представлений.
Возможны и пограничные - динамико-стохастические модели. Например, в уравнениях Лотки - Вольтерры один из параметров - случайная величина с известным законом распределения. Самостоятельные размышления над такими задачами, даже лишь над их постановкой, очень полезны.
Вторая модель, которую опишем во всех деталях, предложена Д.Конвейем -имитационная модель роста, распада и различных изменений в популяции живых организмов, известная под названием «Жизнь».

Рис. 7.48. К имитационной модели «Жизнь»
Для построения алгоритма игры рассмотрим квадратное поле из n +1 столбцов и строк с обычной нумерацией от 0 до n, рис. 7.48. Крайние граничные столбцы и строки для удобства определим как «мертвую зону», они играют лишь вспомогательную роль.
Для любой внутренней клетки поля с координатами (i, j) можто определить 8 соседей. Если клетка «живая», ее закрашиваем, если клетка «мертвая», она пустая.
Зададим правила игры. Если клетка (i, j) «живая» и в окружении более трех «живых» клеток, она погибает (от перенаселения). «Живая» клетка также погибает, если в окружении менее двух «живых» клеток (от одиночества). «Мертвая» клетка оживает, если вокруг нее имеются три «живые» клетки. Для удобства введем двумерный массив А [0. .п, 0. .п ], элементы которого принимают значение 0, если соответствующая клетка пустая, и 1, если клетка «живая». Тогда алгоритм определения состояния клетки с координатой (i,j) можно определить следующим образом:
S:= A[I-1, J-1] + A[I-1, J] + A[I-1, J+1] + A[I+1, J-1]
+ А[I+1, J] + A[I+1, J+l] + A[I, J+l] + А[1, J-1];
If (A[I, J] = 1) And ((S > 3) Or (S < 2); Then B(I, J]:= 0;
If (A[I, J] = 0) And (S = 3) Then B[I, J]:= 1;
Здесь массив В [0. .п, 0. .п ] определяет координаты поля на следующем этапе. Для всех внутренних клеток от i = 1 до n - 1 и j = 1 до n - 1 справедливо сказанное выше. Отметим, что последующие поколения определяются аналогично, лишь стоит осуществить процедуру переприсваивания
For I:= 1 То N-l DO For J:= 1 To N-l Do A[I, J]:= B[I, J];
На экране дисплея удобнее выводить состояние поля не в матричном, а в графическом виде. Читатель без труда это может осуществить. Осталось лишь определить процедуру задания начальной конфигурации игрового поля. При случайном определении начального состояния клеток подходит алгоритм
For I:= 1 То К Do
Begin Kl:= Random(N-l); K2:= Random(N-l)+1; A[K1, K2]:= 1 End;
Интереснее случай, когда начальную конфигурацию мы задаем сами, и удобнее для пользователя делать это непосредственно в графическом виде. Полный текст подобной программы приведен ниже.
Программа 150. «Жизнь».
Program PlayLife;
Uses Crt, Graph; Const R = 41;
Var P; 0..1; А, В: Array[0..R, 0..R] Of 0..1;
I, J, N, Kl, K2, Ss, X, Y, Gm, Gd: Integer; С: Char;
Begin DetectGraph(I, J); InitGraph(I, J, ");
{ -- заставка --)
For I:= 0 To 5 Do
Begin
SetFillStyle (1, I+2); Bar(180+1*10, 100+1*10, 430-1*10, 270-1*10);
End;
OutTextXY(260, 180, 'ИГРА "ЖИЗНЬ"'); Repeat Until KeyPressed;
{ - начальная конфигурация - }
RestoreCrtMode;
For I:= 0 To R Do
For J:= 0 To R Do
Begin A[I, J]:= 0; В[I, J]:= 0 End;
CIrScr;
Write('Начальное поселение будете задавать случайно или вводить (0/1)?'); ReadLn(P);
If P = 0 Then Begin
Write('Введите начальное количество поселений 2 < n < 200: ');
ReadLn(N); Gm:= VgaHi; SetGraphMode(Gm);
For I:= 1 To N Do
Begin
Kl:= Random(R - 1) + 1; K2:= Random(R - 1) + 1;
A{K1, K2]:= 1; B[K1, K2]:= 1;
End;
SetLineStyle(0, 0, 1); SetColor(4);
For I:= 0 To R - 1 Do
Begin
Line(10 + I * 10, 10, 10 + I * 10, R * 10);
Line(10, 10 + I * 10, R * 10, 10 + I * 10);
End;
For I:= 1 To R - 1 Do
For J:= 1 To R - 1 Do
If A[I, J] = 1 Then
FloodFill(5 + I * 10, 5 + J * 10, 4);
Repeat Until KeyPressed;
End
Else
Begin
Gm:= VgaHi; SetGraphMode(Gm); SetLineStyle(0, 0, 1); SetColor(4);
For I:= 0 To R - 1 Do
Begin
Line(10 + I * 10, 10, 10 + I * 10, R * 10);
Line(10, 10 + I * 10, R * 10, 10 + I * 10);
End;
X:= 15; Y:= 15;
Repeat
С:= ReadKey; If С = #0 Then С:= ReadKey;
Case C Of
#72: Begin
SetColor(O); Circle(X, Y, 2); Y:= Y - 10; SetColor(15);
Circle(X, Y, 2)
End;
#80: Begin
SetColor(O); Circle(X, Y, 2); Y:= У + 10; SecColor(15);
Circle(X, Y, 2)
End;
#75: Begin
SetColor(O); Circle(X, Y, 2); X:= X - 10; SetColor(15);
Circle(X, Y, 2)
End;
#77: Begin
SetColor(0); Circle(X, Y, 2); X ^ X + 10; SetColor(15);
Circle(X, Y, 2)
End;
#13: Begin
FloodFill(X, Y, 4); A[(X-5) Div 10, (Y-5) Div 10]:= 1;
B[(X - 5) Div 10, (Y - 5) Div 10]:= 1
End;
#32: Begin
SetFillStyled, 0); Bar(X - 4, Y - 4, X + 4, Y + 4);
A[(X - 5) Div 10, (Y - 5) Div 10]:= 0:
B[(X - 5) Div 10, (Y - 5) Div 10]:= 0;
SetFillStyle(1, 15);
End;
End {case};
Until С = #27;
SetColor(0); Circle(X, Y, 2);
End;
SetColor(15); Repeat Until Key Pressed;
OutTextXY(GetMaxX - 400, GetMaxY - 5, 'для продолжения –любая клавиша, выход - s');
{- начало игры -- }
Repeat
For I:= 1 То R - 1 Do
For J:= 1 To R - 1 Do
Begin
Ss: = A[I - 1, J - 1] + A[I - 1, J] + A[I - 1, J + 1];
Ss:= Ss + A(I + 1, J - 1] + A[I + 1, J] + A[I +1, J + 1];
Ss:= Ss + A[I. J + 1] + A[I, J - 1];
If (A[I, J] = 1) And (Ss > 3) Then
Begin
SetFillStyled, 0); Bar(l + I * 10, 1 + J * 10, 9 + I * 10, 9 + J * 10);
B(I, J]:= 0; SetFillStyled, 15)
End;
If (A[I, J] == 1) And (Ss < 2) Then
Begin
SetFillStyled, 0); Bar(l + I * 10, 1 + J * 10, 9 + I * 10, 9 + J * 10);
B[I, J]:= 0; SetFillStyled, 15)
End;
If (A[I, J] = 0) And (Ss = 3) Then
Begin
FloodFill(5 + I * 10, 5 + J * 10, 4); B[I, J]:= 1
End; Delay(20)
End;
For I:= 1 To R - 1 Do
For J:= 1 To R - 1 Do A[I, J] ••= B[I, J];
С:= ReadKey
Until С = 's'; CloseGraph
End.
Теперь приступим к моделированию. Поставим несколько вопросов: какие конфигурации исчезают с течением времени и как быстро? какие структуры могут существовать бесконечно? каковы законы организации структур, их взаимодействия? Перед попыткой ответить на эти вопросы читателю будет полезно поэкспериментировать самому. Предварительно отметим лишь некоторые структуры (рис. 7.49-7.50).

Рис. 7.49. Стационарные структуры, не зависящие от времени
Существуют структуры, которые повторяют себя через 1, 2, ...,п временных шагов, их называют циклами «- n» (см. рис. 7.50).

Рис. 7.50. Циклы «- 2»
Но наиболее интересны движущиеся структуры - «планеры», «корабли», «паровозы», их столкновения, «аннигиляции» и зарождение новых структур.
Представляет интерес модель игры в одномерном случае. Здесь имеется один ряд клеток. В некоторых нз них задаем «жизнь». Требуется изучить эволюцию клеток, если заданы правила их существования и зарождения.

Определим сумму значений пяти соседних клеток (самой клетки и двух ближайших к ней слева и справа). На следующем шаге в зависимости от суммы, которая может быть равна 0,1, 2, 3,4, 5, клеткам присваивается значение 0,1,0,0,0,0 или 0, 1,1, 1,0,0.
Пусть X(N) - массив клеток. X(i) = 0, если i-я клетка пустая, и X(i) = 1, если в ('-и клетке имеется «жизнь».
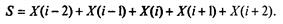
Если Y(N) - массив клеток на следующем временном шаге, то он заполняется, например, по следующему правилу - если S = 1, то Y(i) = 1, иначе Y(i) = 0.
Программа 7.6. «Жизнь на полоске».
Program Lifel;
Uses Crt, Graph; Const N = 60;
Var J, К: Integer; X, Y: Array(O..N] Of 0..1; I, S, Yg: Integer;
P: Real; С: Chart;
Begin
For I:= 0 To N Do Begin X[I]:= 0; Y[I]:= 0 End;
(начальное поселение)
X[N Div 2]:= 1; DetectGraph(J, К); InitGraph(J, К, "); Yg:= 20;
For I:= 0 To N Do If X(I] = 1 Then Circled * 10 + 10, Yg, 2);
Repeat С:= ReadKey; Yg:= Yg + 10;
For I:= 2 To N - 2 Do
Begin
S;= X[I - 2] + X[I - 1] + X[I] + X[I + 1] + X[I + 2];
If S In [1..3] Then Y[I1:= 1
End;
For I:= 0 To N Do
Begin
If Y[I] = 1 Then Circle(I * 10 + 10, Yg, 2); X[I]:= Y[I];
Y[I]:= 0
End
Until С = #27; CloseGraph;
End.
Контрольные вопросы и задания
1. В чем отличие классической экологии от современной?
2. Какие проблемы рассматриваются в классической экологии?
3. Какие виды взаимодействия организмов принято рассматривать в классической экологии?
4. Какие цели преследуются при составлении математических моделей в экологии?
5. В чем выражается специфика биологических систем в отличие от рассмотренных ранее физических и механических систем?
6. Что понимают под конкуренцией в биологии? внутривидовой конкуренцией? межвидовой конкуренцией? Каковы источники конкуренции, и как конкуренция учитывается в приведенных моделях?
7. Какие результаты могут быть получены с помощью простейшей модели роста численности популяции с дискретным размножением? Как изменятся эти результаты, если учесть интенсивность конкуренции?
8. Как построить фазовую диаграмму динамики численности популяции с дискретным размножением?
9. Составьте программу, позволяющую получить все четыре способа изменения численности популяции в модели (7.63).
10. Составьте программу, помогающую построить фазовую диаграмму в модели (7.63).
11. Как выводится логистическое уравнение? Каково аналитическоерешениеэтого уравнения? Как в нем учитывается внутривидовая конкуренция?
12. По какому принципу записывается модель межвидовой конкуренции?
13. Какие результаты могут быть получены с помощью модели межвидовой конкуренции?
14. Какие факторы необходимо учесть при разработке модели системы «хищник -жертва»?
15. Какие результаты могут быть получены с помощью модели «хищник-жертва»?
16. Является ли использование стохастических моделей в исследовании эволюции популяций отражением закономерностей реального мира? В какой мере случайность проявляется в биологических процессах?
17. Получите самостоятельно все результаты, которые приведены в примерах динамики численности популяций с непрерывным размножением и в системе «хищник-жертва», разработав компьютерные программы.
18. Разработайте модель межвидовой конкуренции длятрех популяций. Исследуйте ее с помощью компьютерного моделирования.
19. Предусмотрите в модели «хищник-жертва» случайные внешние воздействия, приводящие к изменению численности популяций.
20. Имеется популяция с непрерывным размножением. В течение некоторого времени через равные промежутки часть особей изымается из популяции (собирается «урожай»). При последнем сборе все особи изымаются. Составьте такой план сбора урожая, чтобы суммарный урожай был максимальным. После очередного сбора популяция не должна вымирать. Разработайте соответствующую моделирующую программу.






