То, что тела могут проводить тепло, общеизвестно. Если один из концов длинного стержня поместить в костер, то, если стержень сделан не из горючего или легко плавящегося материала, другой конец через некоторое время тоже нагреется; как быстро и насколько - зависит от материала, размеров стержня и других факторов. Процесс теплопроводности - один из, так называемых, процессов тепломассопереноса, играющих огромную роль в природе и в технике. Другие процессы такого рода - диффузия, благодаря которой смешиваются разные жидкости или газы, процессы гидро- и аэродинамики (т.е. переноса (движения) жидкостей и газов).
Хотя каждый изтаких процессов имеет собственные закономерности, междуними много общего.Эти процессы происходят в сплошной среде, о которой шла речь выше; при их математическом моделировании используется один и тотжематематический аппарат-дифференциальные уравнения в частных производных.
Ограничимся одной из самых простых задач данного класса - переносом тепла в однородном стержне. Рассмотрим линейный стержень, боковая поверхность которого не проводит тепла (теплонзолирована). Если в начальный момент стержень неравномерно нагрет, то в нем будет происходить перераспределение тепла; при отсутствии внутренних источников тепла его температура, в конце концов, выровняется.
Поскольку стержень линеен и однороден, то распределение температуры в пространстве характеризуется одной координатой x.
Температура (обозначим ее u) зависит от х; кроме того, она может менятьсясовременем, т.е. является функций двух переменных и(х, t). Изменение этой функции вдоль стержня, «скорость» которого определяется производной пол x, и изменение ее со временем, скорость которого определяется производной по t, взаимосвязаныи,как будет показано ниже, входят в одно уравнение.
Уравнение теплопроводности. Получим уравнение, описывающее процесс изменения температуры в стержне. Фиксируем некоторую точку x0 (рис. 7.29) и выделим около нее малый участок стержня длиной Δx. Искомое уравнение есть по существу уравнение теплового баланса (т.е. сохранения энергии): изменение количества тепла в избранном участке стержня за счет притока и (или) оттока его через два сечения приведет к нагреванию или охлаждению этого участка в соответствии с его теплоемкостью. Выразим все это математическим языком.
Рис. 7.29. Участок линейного стержня
Количество тепла, проходящее через поперечное сечение стержня в точке x0 за время Δt, пропорционально площади поперечного сечения S, градиенту температуры 
и промежутку времени Δt: 
~ 
, рис. 7.30. Если с S и Δt все очевидно, то появление производной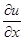 
требует пояснении. За ней стоит тот экспериментальный факт, что поток тепла ΔQ, через некоторый участок стержня длиной Δх тем больше, чем больше разность температур (|и1 | - | u2 |) на его концах и чем меньше расстояние Δх:
Вводя коэффициент пропорциональности k, называемый коэффициентом теплопроводности, получаем
Значение k определяется материалом стержня и для нескольких материалов приведено в табл. 7.6 (в единицах системы СИ: 
).
Таким образом, различия в теплопроводности разных материалов огромны.
Рис. 7.30. Поток тепла через участок стержня длиной Δх
Теперь запишем количество тепла, проходящее через сечение в точке х = x 0 + Δx:. Оно определяется, естественно, той же формулой:
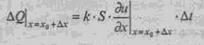
с условием, что производная берется в точке х = x 0 + Δх. Для получения искомого уравнения ее надо выразить через значение в точке x0.
Таблица 7.6
