8 Порядок выполнения домашних работ
Номер варианта задания определяется в соответствие с порядковым номером студента в ведомости, варианты заданий приведены в таблицах 5-10, Таблицы 4 и 5 являются общими для выполнения заданий 1 и 2. В соответствии с учебным планом выполняется следующие 3 задания:
- решение типовых задач алгебры, анализа и в Matlab;
- решение типовых задач алгебры и анализа в символьной форме
- исследование линейной динамической системы в Matlab и Simulink.
Все задания выполняются в соответствии с примерами, приведенными в методических рекомендациях. Выполненные задания, представляются в электронном и бумажном виде. Пример обложки для оформления задания приведен в приложении А.
8.1 Порядок выполнения домашней работы № 1
1 решить систему линейных алгебраических уравнений (п. 2.1);
2 решить дифференциальное уравнение (п. 2.2);
3 вычислить определенный интеграл (п. 2.3 и 2.4) методами трапеций и квадратур;
4 выполнить кубическую интерполяция функции одной переменной (п. 2.5.1);
5 выполнить интерполяцию функции кубическим сплайном (п. 2.5.2);
6 выполнить одномерную табличную интерполяция (п. 2.5.3);
7 выполнить аппроксимацию табличных данных на основе быстрого преобразования Фурье (п. 2.5.4).
8.2 Порядок выполнения домашней работы № 2
1 вычислить символьными методами предел функции (п. 3.2);
2 решить символьными методами алгебраическое уравнение (п. 3.3);
3 произвести дифференцирование функции в символьном виде (п.3.4), кроме того к указанной функции применить 3-х кратное дифференцирование.
4 решить в символьном виде дифференциальное уравнение (п. 3.5);
5 вычислить в символьном виде неопределенный и определенный интегралы (п. 2.3 и 2.4).
8.3 Порядок выполнения домашней работы № 3
1 по данным таблицы 16 получить эквивалентную передаточную функцию средствами Matlab (п. 4.1);
2 произвести исследование линейной системы средствами Matlab (п. 5);
3 в соответствии данным таблицы 16 собрать структурную схему системы в Simulink (п. 6 и 7.1);
4 произвести исследование линейной системы средствами Simulink (п. 7.2);
9 Варианты заданий для выполнения домашних работ
Варианты заданий для решения систем линейных алгебраических уравнений вида А*Х = В и дифференциальных уравнений вида 
, вычисления интегралов и интерполяции и аппроксимации данных представлены в таблицах 9 -12, соответственно. Вариант в таблице 12 значений функции f(x), начиная с узла, равного номеру вашего варианта и заканчивается на номере перед следующим вариантом (например вариант № 13 начинается со значений Х = 13 и заканчивается значением Х=13.9).
Таблица 9 – Варианты заданий для решения систем алгебраических уравнений
| № вар | A | B | № вар | A | B | ||||||
| 0.47 | -0.11 | 0.55 | 1.33 | 0.63 | 0.11 | 0.34 | 2.08 | ||||
| 0.42 | 0.35 | 0.17 | 1.29 | 0.17 | 1.18 | -0.45 | 0.11 | 0.17 | |||
| -0.25 | 0.67 | 0.36 | 2.11 | 0.31 | -0.15 | 1.17 | -2.35 | 1.28 | |||
| 0.54 | -0.32 | -0.74 | 0.10 | 0.58 | 0.21 | -3.45 | -1.18 | 0.05 | |||
| 0.77 | 0.04 | -0.21 | 0.18 | 1.24 | 0.79 | -0.12 | 0.34 | 0.16 | -0.64 | ||
| -0.45 | 1.23 | -0.06 | -0.88 | -0.34 | 1.18 | -0.17 | 0.18 | 1.42 | |||
| -0.26 | -0.34 | 1.11 | 0.62 | -0.16 | -0.34 | 0.85 | 0.31 | -0.42 | |||
| -0.05 | 0.26 | -0.34 | 1.12 | -1.17 | -0.12 | 0.26 | 0.08 | 0.75 | 0.83 | ||
| -0.68 | -0.18 | 0.02 | 0.21 | -1.83 | -0.58 | -0.32 | 0.03 | -0.44 | |||
| 0.16 | -0.88 | -0.14 | 0.27 | 0.65 | 0.11 | -1.26 | -0.36 | -1.42 | |||
| 0.37 | 0.27 | -1.02 | -0.24 | -2.23 | 0.12 | 0.08 | -1.14 | -0.24 | 0.83 | ||
| 0.12 | 0.21 | -0.18 | -0.75 | 1.13 | 0.15 | -0.35 | -0.18 | 1.42 | |||
| -0.83 | 0.31 | -0.18 | 0.22 | 1.71 | -0.87 | 0.27 | -0.22 | -0.18 | -1.21 | ||
| -0.21 | -0.67 | 0.22 | -0.62 | -0.21 | -1. | -0.45 | 0.18 | 0.33 | |||
| 0.32 | -0.18 | -0.95 | -0.19 | 0.89 | 0.12 | 0.13 | -0.33 | 0.18 | 0.48 | ||
| 0.12 | 0.28 | -0.14 | -1 | -0.94 | 0.33 | -0.41 | -1 | 1.21 | |||
| -0.81 | -0.07 | 0.38 | -0.21 | 0.81 | -1 | 0.22 | -0.11 | 0.31 | -2.7 | ||
| -0.22 | -0.92 | 0.11 | 0.33 | 0.64 | 0.38 | -1 | -0.12 | 0.22 | 1.5 | ||
| 0.51 | -0.07 | -0.81 | -0.11 | 1.71 | 0.11 | 0.23 | -0.51 | 1.2 | |||
| 0.33 | -0.41 | -1 | 1.21 | 0.17 | -0.21 | 0.31 | -1 | 0.17 | |||
| -0.93 | -0.08 | 0.11 | -1.18 | 0.51 | -0.95 | -0.06 | -0.12 | 0.14 | 2.17 | ||
| 0.18 | -0.48 | 0.21 | -1.17 | 0.04 | -1.12 | 0.08 | 0.11 | 1.4 | |||
| 0.13 | 0.31 | -1 | -0.21 | 1.02 | 0.11 | 0.12 | 1.03 | 0.8 | |||
| 0.08 | -0.33 | -0.72 | 0.28 | 0.34 | 0.08 | -1.06 | 0.14 | 2.1 | |||
| -0.19 | 0.27 | -0.88 | 1.2 | -0.88 | -0.23 | 0.25 | -0.16 | 1.24 | |||
| -0.33 | -1 | -0.07 | 0.21 | 0.92 | 0.33 | 0.03 | -0.84 | -0.32 | -1.15 | ||
| 0.11 | 1.03 | -0.42 | 0.92 | 0.14 | -0.66 | -0.18 | 0.24 | 0.89 | |||
| -0.92 | -0.03 | -0.04 | 1.2 | 0.12 | -0.05 | -0.85 | 0.57 | ||||
| 0.12 | -1 | 0.32 | -0.18 | 0.72 | -0.86 | 0.23 | 0.18 | 0.17 | 1.42 | ||
| 0.08 | -0.12 | -0.77 | 0.32 | 0.58 | 0.12 | -1.14 | 0.08 | 0.09 | 0.83 | ||
| 0.25 | 0.22 | 0.14 | -1 | -1.56 | 0.16 | 0.24 | -1 | -0.35 | -1.21 | ||
| -0.77 | -0.14 | 0.06 | -0.12 | -1.21 | 0.23 | -0.08 | 0.05 | -0.75 | -0.65 | ||
| -34 | -142 | -83 | -13 | -11 | |||||||
| -114 | -68 | ||||||||||
| -100 | -35 | -121 | |||||||||
| -75 | |||||||||||
| 1.11 | -1 | 0.28 | -0.17 | 0.06 | -21 | ||||||
| 1.16 | 0.52 | -1 | 0.12 | 0.17 | |||||||
| 1.24 | 0.17 | -0.18 | -0.79 | 0.81 | |||||||
| 1.55 | 0.11 | 0.22 | 0.03 | -0.95 | -0.72 |
Таблица 10 - Варианты заданий для решения дифференциальных уравнений
| № вар |  
| 
| 
| 
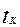
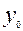
| № вар |
|
|
|
|
 
| 
| ||||||||
| 
| ||||||||
| 
| ||||||||
| 
| 
| |||||||
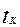
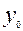
| 1/e | 
| 1/e | ||||||
| 
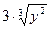
| 0.9 | |||||||
| 
| ||||||||
| 0.5 | 
| |||||||
| 
| ||||||||
| 
|
|
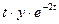
Таблица 11 –Варианты заданий для вычисления интегралов
| № варианта | Подинтегральная функция f(x) | Пределы интегрирования | № варианта | Подинтегральная функция f(x) | Пределы интегрирования | ||
| a | b | a | b | ||||
| 3,5 | 
| |||||
| 
| ||||||
| 2,5 | 
| |||||
| 
| ||||||
| 
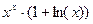
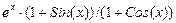
| 1,5 | |||||
| 1,5 | 
| 0,8 | ||||
| 
| ||||||
| 
| ||||||
| 1,8 | 
| |||||
| 
|
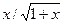
Таблица 12 - Варианты заданий для интерполяции и аппроксимации данных
| x | y(x) | x | y(x) | x | y(x) | x | y(x) |
| 1,0 | 2,0 | 4,62·10-5 | 3,0 | -0,00011 | 4,0 | 0,000196 | |
| 1,1 | 0,324097 | 2,1 | -0,44776 | 3,1 | 0,543966 | 4,1 | -5,19505 |
| 1,2 | 0,643881 | 2,2 | -0,87178 | 3,2 | 1,051358 | 4,2 | -10,3689 |
| 1,3 | 0,922415 | 2,3 | -1,2269 | 3,3 | 1,469572 | 4,3 | -14,959 |
| 1,4 | 1,1253 | 2,4 | -1,47335 | 3,4 | 1,753617 | 4,4 | -18,4126 |
| 1,5 | 1,224745 | 2,5 | -1,58114 | 3,5 | 1,870829 | 4,5 | -20,25 |
| 1,6 | 1,20301 | 2,6 | -1,53356 | 3,6 | 1,804553 | 4,6 | -20,1243 |
| 1,7 | 1,054847 | 2,7 | -1,3294 | 3,7 | 1,556275 | 4,7 | -17,8711 |
| 1,8 | 0,788625 | 2,8 | -0,98363 | 3,8 | 1,145949 | 4,8 | -13,5425 |
| 1,9 | 0,425989 | 2,9 | -0,52634 | 3,9 | 0,610438 | 4,9 | -7,41942 |
| 5,0 | 6,0 | 0,001176 | 7,0 | 0,00018 | 8,0 | -9,6·10-5 | |
| 5,1 | 8,037451 | 6,1 | -11,4973 | 7,1 | 0,856485 | 8,1 | -0,91714 |
| 5,2 | 15,89357 | 6,2 | -22,5932 | 7,2 | 1,640842 | 8,2 | -1,75557 |
| 5,3 | 22,72513 | 6,3 | -32,1089 | 7,3 | 2,27459 | 8,3 | -2,43156 |
| 5,4 | 27,73269 | 6,4 | -38,9547 | 7,4 | 2,692863 | 8,4 | -2,8763 |
| 5,5 | 30,25 | 6,5 | -42,25 | 7,5 | 2,851227 | 8,5 | -3,04297 |
| 5,6 | 29,82532 | 6,6 | -41,4287 | 7,6 | 2,730379 | 8,6 | -2,91168 |
| 5,7 | 26,2854 | 6,7 | -36,3182 | 7,7 | 2,338403 | 8,7 | -2,49175 |
| 5,8 | 19,77381 | 6,8 | -27,1814 | 7,8 | 1,710348 | 8,8 | -1,82115 |
| 5,9 | 10,75785 | 6,9 | -14,7151 | 7,9 | 0,905108 | 8,9 | -0,96308 |
| 9,0 | -10-13 | 10,0 | 0,000108 | 11,0 | -0,00023 | 12,0 | 0,000357 |
| 9,1 | 0,97427 | 10,1 | -1,02845 | 11,1 | 1,080087 | 12,1 | -1,12952 |
| 9,2 | 1,863736 | 10,2 | -1,96638 | 11,2 | 2,064282 | 12,2 | -2,15806 |
| 9,3 | 2,579679 | 10,3 | -2,72032 | 11,3 | 2,854531 | 12,3 | -2,98314 |
| 9,4 | 3,049516 | 10,4 | -3,21408 | 11,4 | 3,37121 | 12,4 | -3,52184 |
| 9,5 | 3,224158 | 10,5 | -3,3964 | 11,5 | 3,560925 | 12,5 | -3,71872 |
| 9,6 | 3,083118 | 10,6 | -3,24618 | 11,6 | 3,402017 | 12,6 | -3,55153 |
| 9,7 | 2,636854 | 10,7 | -2,77495 | 11,7 | 2,90698 | 12,7 | -3,03371 |
| 9,8 | 1,926069 | 10,8 | -2,02598 | 11,8 | 2,121544 | 12,8 | -2,21331 |
| 9,9 | 1,01801 | 10,9 | -1,07035 | 11,9 | 1,120452 | 12,9 | -1,16858 |
| 13,0 | -0,00055 | 14,0 | 0,000735 | 15,0 | -0,00091 | 16,0 | 0,001095 |
| 13,1 | 0,447264 | 14,1 | -0,54336 | 15,1 | 0,624825 | 16,1 | -0,6968 |
| 13,2 | 0,871348 | 14,2 | -1,05084 | 15,2 | 1,203832 | 16,2 | -1,33944 |
| 13,3 | 1,226577 | 14,3 | -1,46919 | 15,3 | 1,677044 | 16,3 | -1,86182 |
| 13,4 | 1,473176 | 14,4 | -1,75341 | 15,4 | 1,994648 | 16,4 | -2,20969 |
| 13,5 | 1,581139 | 14,5 | -1,87083 | 15,5 | 2,12132 | 16,5 | -2,34521 |
| 13,6 | 1,533737 | 14,6 | -1,80476 | 15,6 | 2,040105 | 16,6 | -2,25098 |
| 13,7 | 1,329751 | 14,7 | -1,55668 | 15,7 | 1,754519 | 16,7 | -1,93222 |
| 13,8 | 0,984119 | 14,8 | -1,14651 | 15,8 | 1,288629 | 16,8 | -1,41658 |
| 13,9 | 0,526919 | 14,9 | -0,61111 | 15,9 | 0,685062 | 16,9 | -0,7518 |
Продолжение таблицы 12
| x | y(x) | x | y(x) | x | y(x) | x | y(x) |
| 17,0 | -0,00128 | 18,0 | 19,0 | -0,00059 | 20,0 | 0,000974 | |
| 17,1 | 0,761981 | 18,1 | -0,06906 | 19,1 | 0,328168 | 20,1 | -0,49956 |
| 17,2 | 1,462508 | 18,2 | -0,20633 | 19,2 | 0,661197 | 20,2 | -0,98043 |
| 17,3 | 2,029831 | 18,3 | -0,36975 | 19,3 | 0,95903 | 20,3 | -1,38957 |
| 17,4 | 2,405585 | 18,4 | -0,52416 | 19,4 | 1,183327 | 20,4 | -1,67979 |
| 17,5 | 2,549509 | 18,5 | -0,63728 | 19,5 | 1,301545 | 20,5 | -1,8141 |
| 17,6 | 2,443738 | 18,6 | -0,68247 | 19,6 | 1,29113 | 20,6 | -1,77023 |
| 17,7 | 2,094918 | 18,7 | -0,64188 | 19,7 | 1,142726 | 20,7 | -1,54364 |
| 17,8 | 1,533913 | 18,8 | -0,50883 | 19,8 | 0,86201 | 20,8 | -1,14883 |
| 17,9 | 0,8131 | 18,9 | -0,28908 | 19,9 | 0,46989 | 20,9 | -0,6186 |
Варианты заданий для вычисления пределов функций, решения систем алгебраических уравнений, вычисления производных представлены в таблицах 13, 14 и 15 соответственно.
Таблица 13 –Варианты заданий для вычисления пределов функций
| № варианта | Вид функционального ряда | № варианта | Вид функционального ряда |
| 1
| 
| 
| |
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
|
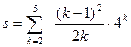
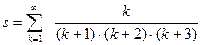
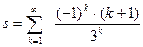
Таблица 14 –Варианты заданий для решения систем алгебраических уравнений
