3.1. Общие положения
Математическими моделями динамических систем автоматического управления являются дифференциальные уравнения. Решение этих уравнений с помощью аналоговых вычислительных машин (АВМ) представляет собой способ получения информации о поведении системы методом машинного моделирования. Существуют два различных подхода к решению задач на АВМ.
В первом случае АВМ используется для чисто математического моделирования исследуемой системы дифференциальных уравнений без отражения в модели реальной структуры объекта (способ непосредственного интегрирования).
Во втором случае АВМ используется для построения структурной модели, представляющей собой аналог, решающие элементы которого соединены между собой в соответствии с алгоритмической схемой исследуемой системы (структурный способ).
При исследовании структурного способа модель системы представляется в виде блоков, имитирующих работу отдельных физических узлов (электрических машин, усилителей, регуляторов, датчиков и т. д.), причём каждый блок выполняется из моделей типовых динамических звеньев.
Таким образом, структурное моделирование предполагает воспроизведение структуры объекта, управляющего устройства и других элементов системы, которые представляются комбинацией элементарных звеньев.
Целесообразность применения структурных моделей связана с тем, что при исследовании на АВМ сохраняется структура исследуемого объекта, и поэтому на модели легко воспроизводится изменение отдельных параметров и способов соединения элементов, необходимое для обеспечения определённого качества переходного процесса системы.
При использовании способа непосредственного интегрирования исходное дифференциальное уравнение должно быть преобразовано к виду, наиболее удобному для исследования на модели.
При использовании структурного способа каждое типовое звено, описываемое дифференциальным уравнением, также должно быть представлено в виде, наиболее удобном для исследования на модели и для стыковки звеньев друг с другом при «замыкании» системы.
И в том, и в другом случаях для решения дифференциальных уравнений с помощью аппаратных технических средств используют следующие методы решения, выбор которых зависит от типа дифференциальных уравнений и от конкретных задач, стоящих перед исследователем:
1) общий метод решения дифференциальных уравнений при помощи понижения порядка производной (метод последовательного интегрирования);
2) метод канонической формы;
3) метод вспомогательной переменной.
3.2. Общий метод решения дифференциальных уравнений
Реализацию этого метода рассмотрим на примере решения дифференциального уравнения второго порядка
|
(3.1)
с нулевыми начальными условиями.
Суть метода состоит в том, что уравнение разрешают относительно старшей производной:
|
(3.2)
В вычислительной машине математические операции, заданные исходными уравнениями, выполняются над машинными переменными,
поставленными в соответствии с переменными исходного уравнения. В АВМ машинными переменными являются электрические напряжения. Таким образом, переменным 
уравнения (3.2) в АВМ будут соответствовать напряжения 
Согласно теории подобия между машинными и исходными переменными должна существовать однозначная линейная зависимость, определяемая масштабами. Поэтому уравнение (3.2) заменяется машинным:
(3.3)
Напряжение, соответствующее старшей производной, равно сумме напряжений, каждое из которых, кроме 
, можно получить интегрированием суммарного напряжения (рис.3.1). Напряжение 
поступает в схему извне. Напряжение, соответствующее решению дифференциального уравнения, будет наблюдаться на выходе последнего интегратора.
Рис.3.1. Блок-схема решения дифференциального уравнения общим методом понижения порядка производной
В практических задачах процесс решения сложнее, так как обычно имеются ненулевые начальные условия, входное воздействие может представлять собой сложную функцию времени, требуется учёт изменения знаков переменных, учёт нелинейностей и т. д.
Достоинствами общего метода решения дифференциальных уравнений являются простота и наглядность решения задачи, возможность задания начальных условий.
Недостатком метода является то, что его нельзя применять, если правая часть уравнения содержит производные входной переменной X. Применение метода к уравнениям такого типа приведёт к появлению в схеме модели дифференцирующих элементов, усиливающих шумы и помехи, спектр которых содержит более высокие частоты, чем спектр полезного сигнала. Кроме того, при решении уравнения высокого порядка на сумматоре (см. рис.3.1) будет слишком много входов, что приведёт к понижению точности решения задачи.
3.3. Решение дифференциальных уравнений методом канонической формы
Реализацию этого метода рассмотрим на примере решения дифференциального уравнения второго порядка с производными в правой части
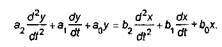(3.4)
Суть метода состоит в том, что исходное уравнение разрешают относительно искомой переменной у Для этого уравнение (3.4) записывают в операторной форме
(3.5)
а затем все члены уравнения (3.5) делят на «а2р2»:
(3.6)
Разрешим уравнение (3.6) относительно «у» и сгруппируем переменные:
(3.7) 29
или в другой форме
(3.8)
Заменим уравнение (3.8) машинным
(3.9)
Обозначим
(3.10)
с учётом (3.10) перепишем уравнение (3.9)
|
(3.11)
Рис.3.2. Блок-схема решения дифференциального уравнения методом канонической формы
Достоинства метода в том, что он позволяет решать диффе-ренциальные уравнения, содержащие производные в правой части, ив том, что на каждый блок приходится не более трёх входов вне зависимости от порядка решаемого уравнения (рис.3.2). Недостатками являются малая физичность, ненаглядность и невозможность задания начальных условий.
3.4. Решение дифференциальных уравнений методом вспомогательной переменной
Реализацию этого метода рассмотрим на примере решения вышеприведённого (3.4) дифференциального уравнения второго порядка с производными в правой части.
Запишем уравнение в операторной форме
(3.12) и разрешим его относительно искомой переменной 
(3.13)
Далее вводится вспомогательная переменная 
, равная
входной величине делённой на полином знаменателя выражения (3.13)
(3.14)
Освободившись от знаменателя и учитывая, что 
, получим
(3.15) После выделения в (3.15) старшей производной по Z получим
(3,16)
Из выражения (3.13) с учётом (3.14) следует, что
(3.17) Выражения (3.16) и (3.17) образуют решающую систему (рис.3.3)
(3.18)
Достоинство метода вспомогательной переменной в том, что он нагляден, даёт возможность изменять коэффициенты левой и правой частей исходного уравнения (3.12) независимо друг от друга.
Кроме того, попутно получаем решение уравнения без производных в правой части 
Недостаток - в возможном снижении точности
решения из-за большого числа входов на сумматорах при высоком порядке дифференциального уравнения.
Рис.3.3. Блок-схема решения дифференциального уравнения методом вспомогательной переменной
Для реализации машинной модели в соответствии с блок-схемами на рис. 3.1-3.3 необходима техническая реализация операций интегрирования, суммирования, умножения на постоянные коэффициенты. Линейные решающие блоки являются основными блоками для реализации математических операций на АВМ.
3.5. Линейные решающие блоки АВМ
В АВМ основным элементом решающих блоков является операционный усилитель (ОУ). Большинство современных ОУ построены по схеме дифференциального усилителя и имеют один несимметричный выход и два дифференциальных входа по отношению к общему проводу («земле») (рис.3.4,а). Коэффициенты усиления по каждому входу равны, но противоположны по знаку. Вход, отмеченный знаком «минус», называется инвертирующим. Это значит, что полярность выходного напряжения противоположна по отношению к напряжению, приложенному к инвертирующему блоку. Вход, отмеченный знаком «плюс», -неинвертирующий.
На схемах аналогового моделирования при изображении ОУ неиспользуемый неинвертирующий вход обычно не изображается
(рис.3.4,6).
Рис.3.4. Операционный усилитель Решающие блоки АВМ построены на основе ОУ с большим
5 7
коэффициентом усиления (10 -10), охваченного отрицательной обратной связью. Для обеспечения отрицательной обратной связи в ОУ используется инвертирующий вход, и любая цепь, передающая сигнал с выхода на вход, является цепью отрицательной обратной связи (рис.3.5).
Рис.3.5. Схема решающего блока АВМ
На рис.5 показана обобщённая схема решающего блока. Рассмотрим подробнее узел «А» этой схемы. Для любого узла электрической цепи справедлив закон Кирхгофа, согласно которому алгебраическая сумма токов, втекающих и вытекающих из узла, равна нулю. 8 соответствии с этим для узла «А» имеем- 
С учётом того, что входной ток 
при достаточно боль-
шом коэффициенте усиления 
равен нулю (
т. к. напряжение
на входе 
, выразим токи через напряжения и ком-
плексные сопротивления:
(3.19) 33
где 
- комплексные сопротивления соответственно входной
цепи и цепи обратной связи решающего блока.
Узел «А» на рис.3.5 часто называют «потенциально заземлённой» или «суммирующей» точкой схемы.
На основании (3.19) запишем передаточную функцию (ПФ) решающего блока:
(3.20)
где знак «минус» означает, что сигнал 
противоположен по знаку
входному напряжению.
Полученное выражение (3.20) является основой для построения всех линейных решающих блоков. Изменяя комплексные сопротивления входных цепей и цепи обратной связи, можно изменять ПФ решающего блока и реализовывать с помощью ОУ различные динамические звенья.
Рассмотрим частные случаи линейных решающих блоков.
Масштабный блок. В этом случае (рис.3.6,а) во входной цепи или цепи обратной связи стоят резисторы и ПФ блока равна
(3.21)
Очень часто в аналоговом моделировании применяется звено с передаточной функцией 
. Такой блок называют блоком
перемены знака, при этом 
. При 
получается усиление
или ослабление сигнала, сопровождаемое инвертированием, т. е умножение на постоянное число с изменением знака.
Сумматор. Выходное напряжение сумматора с тремя входами (рис.3.6,6) может быть определено на основании (3.20)
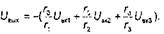(3.22)
Интегратор. Передаточная функция решающего блока (рис.З.6.е) согласно (3.20) выражается формулой;
(3.23)
где 
Интегро-сумматор. Многие линейные операции достаточно просто совмещаются в одном решающем блоке. Примером такого совмещения является суммирование и интегрирование на одном ОУ. На рис.З.б.з приведена схема для выполнения операции суммирования трёх сигналов с последующим интегрированием. Выходное напряжение схемы, определённое на основании (3.20) и (3.23), равно
(3.24)
где 
Как и в случае сумматора, сигналы в этой схеме могут складываться с одинаковыми или с разными весами.
Рис.3.6. Реализация линейных математических операций в решающих блоках ASM
3.6. Масштабирование переменных
Одним из наиболее важных этапов подготовки задач для решения на АВМ является масштабирование. Переменные исходной задачи могут быть как величинами безразмерными, так и иметь размерность. В АВМ всем исходным переменным ставятся в соответствие электрические напряжения, которые называются машинными переменными. За независимую переменную в АВМ принято время Переход от переменных исходной математической или физической задачи к их аналогам в АВМ и представляет сущность операции масштабирования, осуществляемого путём введения масштабов.
Масштабы зависимых переменных имеют размерность
Эти масштабы позволяют представить машинные переменные АВМ 
и 
в виде:
(3.25)
где 
- возмущения и зависимые переменные исходной
задачи, а 
- их масштабы.
При выборе масштабов зависимых переменных в основном руководствуются требованиями наилучшего соответствия диапазона изменения исходной переменной с диапазоном линейности 
усилителей АВМ. Для многих АВМ этот диапазон составляет 100 В, Основанием для выбора масштабов зависимых переменных 
и возмущений 
являются соотношения
(3.26)
Знак «меньше» в указанных соотношениях относится к случаю округления (когда необходимо) величины масштаба до ближайшего меньшего числа вида: 
где 
- целое число.
Использование таких чисел в качестве масштабов облегчает проведение расчётов, связанных с переходом от машинных переменных к исходным и обратно.
Как следует из (3.26), для выбора масштабов надо знать максимальные значения воздействий и переменных в исходной задаче.
При моделировании замкнутых контуров систем управления часто удаётся обойтись без масштабирования зависимых переменных, перераспределив передаточные коэффициенты элементов системы между собой.
Обычно при выборе масштабов зависимых переменных составляют специальную таблицу.
В качестве примера рассмотрим процедуру ввода масштабов зависимых переменных для дифференциального уравнения, описывающего колебательную систему (рис.3.7):
(3.27)
где т - масса груза; о - коэффициент сил вязкого трения; с - жёсткость пружины; у - отклонение груза от положения равновесия (перемещение); 
- сила, действующая на груз.
В уравнении (3.27) 
- скорость, а 
- ускорение
перемещения груза.
Рис.3.7. Колебательная система 37
В табл.3.1 приведены все данные, необходимые для определения масштабов зависимых переменных. В третьей колонке указаны максимально возможные численные значения зависимых переменных. Если они неизвестны, то их принимают ориентировочно, а затем в процессе решения уточняют, пересчитывая при этом масштабные множители.
В четвёртой колонке табл. 3.1 определены численные значения масштабов с учётом условия (3.26). Чтобы ввести масштабные множители в уравнение (3.27), необходимо выполнить операцию согласования масштабов, состоящую в том, что машинный коэффициент исходной системы умножается на масштаб выходной величины и делится на масштаб входной величины.
Схема модели решающего уравнения (3.27) приведена на рис.3.8,а.
Введём масштабы зависимых переменных и получим модель, приведённую на рис.3.8, б. При этом машинные коэффициенты 
определены следующим образом:
,-ис.З -Z. Аналоговая модель колебательной еистемы;
а) без учёта масштабов зависимых переменных;
б) с учетом масштабов зависимых переменных;
в) с выделением старшей производной
В случае, если необходимо в явном виде контролировать сигнал, модель уравнения (3.27) примет вид, изображённый на рис.3.8,е. В этом случае машинные коэффициенты с учётом масштабов зависимых переменных будут иметь вид:
Из этого следует, что введение масштабов зависимых переменных не меняет структуры модели, а лишь изменяет машинные коэффициенты.
Исходной независимой переменной динамических систем является время 
поэтому при их моделировании масштаб времени
(3.28)
представляет собой безразмерную величину, характеризующую соотношения скоростей протекания динамических процессов в модели и исходной системе. В формуле (3.28) 
-машинное время. При 
принято говорить, что процесс протекает в натуральном (реальном) масштабе времени, при 
- в замедленном, при- 
в уско-
ренном времени. Таким образом, масштабирование времени - это изменение продолжительности решения задачи на АВМ. В большинстве случаев решающим при выборе масштаба времени является согласование времени решения задачи с характеристиками регистрирующей и записывающей аппаратуры.
Если имеются сведения о времени протекания процесса fnp в исследуемой системе, то масштаб времени определяется из соотношения:
(3.29)
где 
- время решения задачи на АВМ.
Также, как и в случае выбора масштабов зависимых переменных, полученное численное значение масштаба времени обычно округляется.
Если время протекания процесса неизвестно, то масштаб времени можно выбрать из соотношения:
(3.30) где 
- соответственно свободный член и коэффициент при
старшей производной решаемого дифференциального уравнения; п- порядок уравнения.
При моделировании системы управления по алгоритмической схеме масштаб времени также определяется из соотношения (3.29), а если время протекания процесса в исходной системе неизвестно, то по соотношению (3.30), где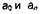 
- соответствующие коэффици-
енты характеристического уравнения замкнутого контура.
При моделировании сильноинерционных замкнутых контуров управления, содержащих запаздывающие звенья, в первом приближении (предполагая 
), масштаб времени можно выбрать по формуле:
(3.31)
где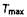 
- максимальная постоянная времени звена, входящего в
систему; 
- время запаздывания.
В конечном счете, правильность выбора масштабов независимой и зависимых переменных заключается в возможности реализации рассчитанных коэффициентов передачи по входам решающих блоков и в удобстве наблюдения и регистрации процесса.
Рассмотрим пример введения масштаба времени в уравнении (3.27). С учётом (3.28) 
Переходя от 
к 
в (3.27) получим
(3.32)
(3.33)
Таким образом, введение масштаба времени изменяет лишь машинные коэффициенты.
4. Цифровое моделирование систем
4.1. Численный метод Эйлера
Основная операция, используемая при моделировании динамических систем, - это решение систем обыкновенных дифференциальных уравнений (ОДУ). Решение ОДУ осуществляется аппаратными техническими средствами при аналоговом моделировании или программными средствами при цифровом моделировании.
Цифровое моделирование систем основано на приближённой замене дифференциальных уравнений, описывающих системы, разностными уравнениями с достаточно малым шагом дискретизации по времени.
Любая система нелинейных ОДУ может быть представлена как система дифференциальных уравнений 1-го порядка в явной форме Коши:
(4.1)
где у - вектор состояния; 
- время; 
- известная функция вре-
мени, дифференцируемая в окрестности точки 
, соответствую-
щей заданному начальному условию 
Самый простой метод приближённого решения (интегрирования) дифференциальных уравнений - метод Эйлера - заключается в том, что для вычисления приближённых значений решения 
в точках
(
- шаг дискретизации) каждое очередное значение искомого решения на /-ом шаге представляют в виде ряда Тейлора, ограничиваясь первыми двумя членами разложения в ряд:
(4.2) где 
{
Приближённое равенство (4.2) называют разностным уравнением, эквивалентным (с погрешностью дискретизации) исходному дифференциальному уравнению (4.1). Разностные уравнения в явной форме
выражают текущие значения 
искомого решения через его пре-
дыдущие значения 
Процедура последовательного решения
уравнения (4.1), в соответствии с алгоритмом (4.2), называется рекуррентной.
Решение ОДУ разностным методом Эйлера даёт удовлетворительные по точности результаты только в тех случаях, когда шаг интегрирования 
достаточно мал по сравнению с темпом изменения функции 
по времени. Для достижения 5 %-ой точности расчётов шаг дискретизации At рекомендуется выбирать из соотношения 
где Т-наименьшая постоянная времени.
Проиллюстрируем применение метода Эйлера к расчёту переходной характеристики инерционного звена 1-го порядка с передаточной функцией (ПФ)
(4.3)
Передаточной функции (4.3) соответствует дифференциальное уравнение:
(4.4)
с нулевыми начальными условиями 
Решим уравнение (4.4) относительно старшей производной
(4.5)
и запишем рекуррентный алгоритм вычисления выходной величины y(t):
(4.6)
В качестве входного сигнала x(t) рассмотрим единичное ступенчатое воздействие:
Тогда
(4.7)
Необходимо отметить, что при цифровом моделировании анализу частотных свойств объектов исследования следует уделять серьёзное внимание, ибо неверно выбранный шаг дискретизации 
может привести не только к большой погрешности расчётов, но и к появлению неустойчивых решений в устойчивых системах.
Решение дифференциальных уравнений, не содержащих производных в правой части (производных входного сигнала), осуществляется методом последовательного интегрирования.
Рассмотрим систему, описываемую ПФ второго порядка
(4.8)
Решим данное дифференциальное уравнение общим методом. Для чего преобразуем ПФ (4.8) к виду:
(4.9)
Избавимся от знаменателя и произведём замену 
(4.10) Решим это уравнение относительно старшей производной (рис.4.1)
(4.11)
Алгоритм приближённого решения (интегрирования) дифференциального уравнения (4.11), используя численный метод Эйлера (рис.4.1):
(4.12)
Определить шаг дискретизации для системы с ПФ (4.8) можно через «эквивалентную» постоянную времени 
(4.13)
Рис.4.1. Схема цифровой модели звена с ПФ (4.8)
Приближённое решение дифференциальных уравнений, содержащих производные в правой части (производные входного сигнала) осуществляется методом вспомогательной переменой.
Рассмотрим систему, описываемую ПФ 3-го порядка вида:
(4.14)
Решим данное дифференциальное уравнение методом вспомогательной переменной. Для чего преобразуем ПФ (4.14) к виду:
(4.15)
Далее вводится вспомогательная переменная, равная входной величине делённой на полином знаменателя ПФ(4.14)
(4.16)
Освободившись от знаменателя и учитывая, что 
, получим
(4.17) После выделения в (4.17) старшей производной по и получим
(4.18) 45
Из выражения (4.15) с учётом (4.16) следует, что
(4.19) Выражения (4.18) и (4.19) образуют решающую систему (рис. 4.2)
(4.20)
Рис.4.2. Схема цифровой модели звена с ПФ (4.14)
Чтобы получить приближённое решение системы дифференциальных уравнений (4.20), используя метод Эйлера, необходимо:
1. Численно решить первое уравнение системы (4.20)
(4.21)
Начальные условия численного интегрирования могут быть следующие (переходный процесс при единичном ступенчатом воздействии):
2. Получив значение вспомогательной переменной и и всех её про
изводных на /-ом шаге, можно решить второе уравнение системы
(4.20) и получить текущее значение выходной координаты V на этом
же шаге рекуррентного алгоритма Эйлера
(4.22)
3. Выполняя пункты 1 и 2 указанного рекуррентного алгоритма в цикле продвижения модельного времени 
с заданным шагом дискре-
тизации 
на отрезке 
, можно приближённо получить характе-
ристику переходного процесса звена с ПФ (4.14).
Алгоритм цифрового моделирования системы, описываемой ПФ (4.14), в соответствии с численным методом Эйлера можно представить в виде блок-схемы, изображённой на рис.4.3.
Рис.4.3. Алгоритм цифрового моделирования звеиа с ПФ (4.14) 47
4.2. Численный метод Рунге-Кутты
Самый простой метод приближённого решения обыкновенных дифференциальных уравнений (ОДУ) - метод Эйлера - заключается в том, что для вычисления приближённых значений решения 
каж-
дое очередное значение искомого решения представляют в виде ряда Тейлора, ограничиваясь первыми двумя членами разложения в ряд:
(4.23)
Для уменьшения погрешности метода интегрирования ОДУ, использующего разложение искомого решения в ряд Тейлора, необходимо учитывать большее количество членов ряда. Однако при этом возникает необходимость аппроксимации производных от правых частей ОДУ.
Основная идея методов Рунге-Кутты заключается в том, что производные аппроксимируются через значения функции 
в
точках на отрезке 
, которые выбираются из условия наи-
большей близости алгоритма к ряду Тейлора (
- шаг дискретизации). В зависимости от старшей степени 
, с которой учитываются члены ряда, построены вычислительные схемы Рунге-Кутты разных порядков точности.
Так, например, для 2-го порядка получено однопараметрическое семейство разностных схем
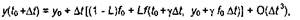(4.24) где 
- свободный параметр; 
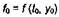- начальное значение
функции времени; 
- бесконечно малая величина,
характеризующая погрешность вычислений.
Для параметра L чаще используют значения L=0,5 и L=1. При L=0,5 формула (4.24) приобретает вид:
(4.25) геометрическая интерпретация (4.25) представлена на рис. 4.4.
Сначала вычисляется приближённое решение ОДУ в точке
по формуле Эйлера 
Затем определяется наклон
интегральной кривой в найденной точке 
, и, после нахождения
среднего наклона на шаге 
определяется уточнённое решение
Схемы подобного типа называются «прогноз-коррекция», что подразумевает грубое вычисление решения по формуле низкого порядка, а затем уточнение с учётом полученной информации о поведении интегральной кривой.
Рис.4.4. Численный метод Рунге-Кутты 2-го порядка (L=0,5)
Рис.4.5. Численный метод Рунге-Кутты 2-го порядка (£.=1) 49
При L=1 от формулы (4.24) переходим к схеме:
(4.26)
геометрический смысл которой отражает рис.4.5.
Здесь при прогнозе решение определяется в точке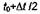 
методом Эйлера 
а после вычисления наклона каса-
тельной к интегральной кривой в средней точке решение корректируется по этому наклону на шаге 
Следует отметить, что численный метод Эйлера требует меньшего размера шага интегрирования 
чем методы Рунге-Кутты, для обеспечения сравнимой точности. При этом, чем ниже порядок метода Рунге-Кутты, тем меньший размер шага 
ему требуется.
4.3. Цифровые модели типовых динамических звеньев
Условные обозначения элементов в схемах цифрового моделирования представлены в табл.4.1.
Таблица 4.1 Цифровые модели типовых динамических звеньев
|
Продолжение табп.4.1
Список литературы
Советов Б. Я, Яковлев С. А. Моделирование систем: Учебник для вузов. 3-е изд., перераб. и доп. М.: Высшая школа, 2001. 343 с.
Фиалко М. Г., Барановский В. П. Моделирование элементов и систем управления. Учебное пособие по дисциплине «Моделирование систем управления». Екатеринбург: УГГГА, 1996. 85 с.
Цыпин Е. Ф., Морозов Ю. П., Козин В. 3. Моделирование обогатительных процессов и схем: Учебник для вузов. Екатеринбург: УГУ, 1996.368 с.
Шеннон Р. Ю. Имитационное моделирование - искусство и наука. М.:Мир, 1978.418 с.
Игорь Сергеевич Бобин
Моделирование систем
Конспект лекций
по дисциплине «Моделирование систем» для студентов
специальности 210200 - «Автоматизация технологических процессов
и производств» (АГП)
Часть 1 Корректура кафедры автоматики и компьютерных технологий
Подписано в печать Бумага писчая. Формат бумаги 60x84 1/16. Печать на ризографе. Печ.л. 3,3, Уч.-изд.л. 2,89. Тираж 50 экз. Заказ №
Издательство УГГА
Лаборатория множительной техники
