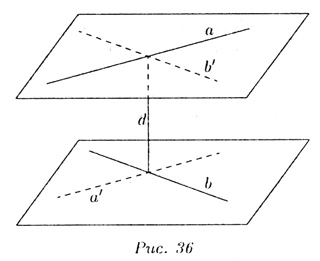
Плоскость, прямая, точка — основные понятия геометрии. Нам трудно дать им четкие определения, однако интуитивно мы понимаем, что это такое. Плоскость имеет только два измерения. У нее нет глубины. Прямая имеет лишь одно измерение, а у точки вообще нет размеров — ни длины, ни ширины, ни высоты.
Плоскость бесконечна. Поэтому в задачах мы рисуем только часть плоскости. Надо же как-то ее изобразить.
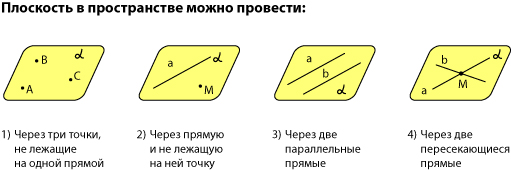
А как все это выглядит в пространстве? Очень просто. Лист плотной бумаги послужит «моделью» плоскости. Можете взять другой плоский предмет, например, CD-диск, пластиковую карту. Карандаши вполне могут изобразить прямые. Все аксиомы и теоремы стереометрии можно показать «на пальцах», то есть с помощью подручных материалов. Читаете — и сразу стройте такую «модель».
Две плоскости в пространстве либо параллельны, либо пересекаются. Примеры в окружающем пространстве найти легко.
Если две плоскости имеют общую точку, то они пересекаются по прямой.
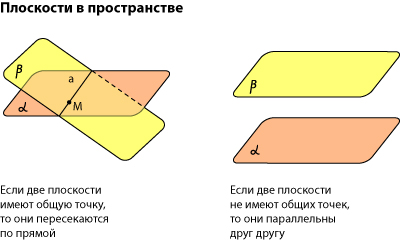
Мы не рассматриваем отдельно случай «плоскости совпадают». Раз совпадают — значит, это одна плоскость, а не две.
Угол между плоскостями
Пусть плоскости 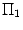 и
и 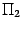 заданы соответственно уравнениями
заданы соответственно уравнениями 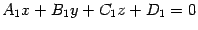 и
и 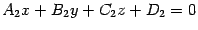 . Требуется найти угол
. Требуется найти угол 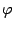 между этими плоскостями.
между этими плоскостями.
Плоскости, пересекаясь, образуют четыре двугранных угла (рис. 11.6): два тупых и два острых или четыре прямых, причем оба тупых угла равны между собой, и оба острых тоже равны между собой. Мы всегда будем искать острый угол. Для определения его величины возьмем точку 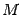 на линии пересечения плоскостей и в этой точке в каждой из плоскостей проведем перпендикуляры
на линии пересечения плоскостей и в этой точке в каждой из плоскостей проведем перпендикуляры 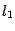 и
и 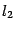 к линии пересечения. Нарисуем также нормальные векторы
к линии пересечения. Нарисуем также нормальные векторы 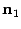 и
и 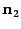 плоскостей
плоскостей 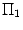 и
и 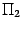 с началами в точке
с началами в точке 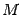 (рис. 11.6).
(рис. 11.6).

Рис.11.6.Угол между плоскостями
Если через точку 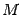 провести плоскость
провести плоскость  , перпендикулярную линии пересечения плоскостей
, перпендикулярную линии пересечения плоскостей 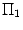 и
и 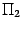 , то прямые
, то прямые 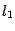 и
и 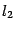 и изображения векторов
и изображения векторов 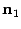 и
и 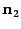 будут лежать в этой плоскости. Сделаем чертеж в плоскости
будут лежать в этой плоскости. Сделаем чертеж в плоскости  (возможны два варианта: рис. 11.7 и 11.8).
(возможны два варианта: рис. 11.7 и 11.8).

Рис.11.7.Угол между нормальными векторами острый

Рис.11.8.Угол между нормальными векторами тупой
В одном варианте (рис. 11.7) 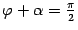 и
и 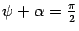 , следовательно, угол
, следовательно, угол 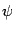 между нормальными векторами равен углу
между нормальными векторами равен углу 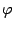 , являющемуся линейным углом острого двугранного угла между плоскостями
, являющемуся линейным углом острого двугранного угла между плоскостями 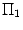 и
и 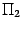 .
.
Во втором варианте (рис. 11.8)  , а угол
, а угол 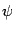 между нормальными векторами равен
между нормальными векторами равен 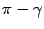 . Так как
. Так как
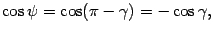
то в обоих случаях 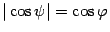 .
.
По определению скалярного произведения 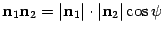 . Откуда
. Откуда
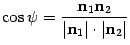
и соответственно

| (11.4) |
Так как координаты нормальных векторов известны, если заданы уравнения плоскостей, то полученная формула (11.4) позволяет найти косинус острого угла между плоскостями.
Если плоскости перпендикулярны, то перпендикулярны и их нормальные векторы. Получаем условие перпендикулярности плоскостей:

| (11.5) |
Если плоскости параллельны, то коллинеарны их нормальные векторы. Получаем условие параллельности плоскостей

| (11.6) |
где  -- любое число.
-- любое число.
23.Различные виды уравнений прямой в пространстве
Векторно-параметрическое уравнение прямой
 где
где  - фиксированная точка, лежащая на прямой; - фиксированная точка, лежащая на прямой; 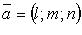 - направляющий вектор.
В координатах (параметрические уравнения): - направляющий вектор.
В координатах (параметрические уравнения):
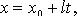
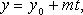
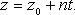 Уравнения прямой по двум точкам
Уравнения прямой по двум точкам
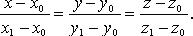 24. Различные виды уравнений прямой в пространстве
Канонические уравнения прямой
24. Различные виды уравнений прямой в пространстве
Канонические уравнения прямой
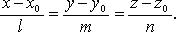 Параметрические уравнения прямой получим, приравняв каждое из отношений (3.4) параметру t:
x = x 1 + mt, y = y 1 + nt, z = z 1 + р t.
25. Взаимное положение прямых
Две прямые в пространстве могут пересекаться, скрещиваться и могут быть параллельны.
1. Пересекающиеся прямые
Пересекающимися прямыми называются такие прямые, которые имеют одну общую точку.
Из инвариантного свойства 5 следует, что проекция точки пересечения проекций прямых а и b есть точка пересечения этих прямых (рис. 3.4).
Параметрические уравнения прямой получим, приравняв каждое из отношений (3.4) параметру t:
x = x 1 + mt, y = y 1 + nt, z = z 1 + р t.
25. Взаимное положение прямых
Две прямые в пространстве могут пересекаться, скрещиваться и могут быть параллельны.
1. Пересекающиеся прямые
Пересекающимися прямыми называются такие прямые, которые имеют одну общую точку.
Из инвариантного свойства 5 следует, что проекция точки пересечения проекций прямых а и b есть точка пересечения этих прямых (рис. 3.4).
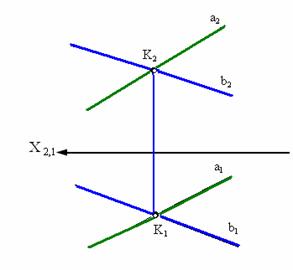 .
Рис. 3.4. Пересекающиеся прямые
2. Параллельные прямые
На рис. 3.5 изображены параллельные прямые – прямые, пересекающиеся в несобственной точке (прямые, лежащие в одной плоскости и пересекающиеся в бесконечно удаленной точке).
Из инвариантного свойства 6 следует, что проекции параллельных прямых а и b параллельны.
3. Скрещивающиеся прямые
Скрещивающиеся прямые – это прямые, не лежащие в одной плоскости, это прямые не имеющие ни одной общей точки.
На комплексном чертеже (рис. 3.6) точки пересечения проекций этих прямых не лежат на одном перпендикуляре к оси Х (в отличие от пересекающихся прямых, см. рис. 3.4). .
Рис. 3.4. Пересекающиеся прямые
2. Параллельные прямые
На рис. 3.5 изображены параллельные прямые – прямые, пересекающиеся в несобственной точке (прямые, лежащие в одной плоскости и пересекающиеся в бесконечно удаленной точке).
Из инвариантного свойства 6 следует, что проекции параллельных прямых а и b параллельны.
3. Скрещивающиеся прямые
Скрещивающиеся прямые – это прямые, не лежащие в одной плоскости, это прямые не имеющие ни одной общей точки.
На комплексном чертеже (рис. 3.6) точки пересечения проекций этих прямых не лежат на одном перпендикуляре к оси Х (в отличие от пересекающихся прямых, см. рис. 3.4).
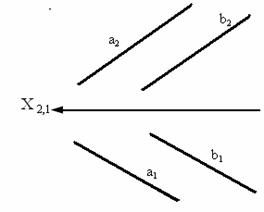 .
Рис. 3.5. Изображение параллельных прямых .
Рис. 3.5. Изображение параллельных прямых
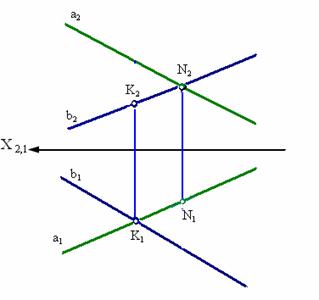 .
Рис. 3.6. Скрещивающиеся прямые
Расстояние от точки до прямой — равно длине перпендикуляра, опущенного из точки на прямую.
Если прямая параллельна плоскости проекции (h | | П1), то для того чтобы определить расстояние от точки А до прямой h необходимо опустить перпендикуляр из точки А на горизонталь h. .
Рис. 3.6. Скрещивающиеся прямые
Расстояние от точки до прямой — равно длине перпендикуляра, опущенного из точки на прямую.
Если прямая параллельна плоскости проекции (h | | П1), то для того чтобы определить расстояние от точки А до прямой h необходимо опустить перпендикуляр из точки А на горизонталь h.
На этом утверждении основана возможность определить расстояние d между двумя скрещивающимися прямыми как расстояние между плоскостями, проведенными через каждые из данных прямых параллельно другой прямой. |





 проходит через а, плоскость проходит через b), параллельная другой прямой.
Отрезки параллельных прямых, заключенные между параллельных прямых, равны.
проходит через а, плоскость проходит через b), параллельная другой прямой.
Отрезки параллельных прямых, заключенные между параллельных прямых, равны.