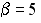I:
S: Если система линейных уравнений  где
где  ,
,  – некоторые числа, имеет бесконечное множество решений, то
– некоторые числа, имеет бесконечное множество решений, то  равно …
равно …
-: – 3
-: – 7
+: 6
-: 5
I:
S: Если система линейных уравнений  где
где 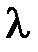 ,
, 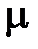 – некоторые числа, имеет бесконечное множество решений, то
– некоторые числа, имеет бесконечное множество решений, то 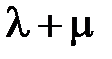 равно …
равно …
-: – 3
+: – 7
-: 6
-: 5
I:
S: Система линейных уравнений 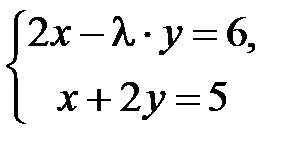 не имеет решений, если
не имеет решений, если 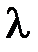 равно …
равно …
-: – 3
-: 4
+: – 4
-: 3
I:
S: Система линейных уравнений 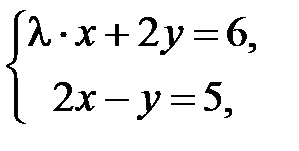 не имеет решений, если
не имеет решений, если 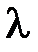 равно …
равно …
-: – 4
-: 2
+: – 2
-: 4
I:
S: Система линейных уравнений 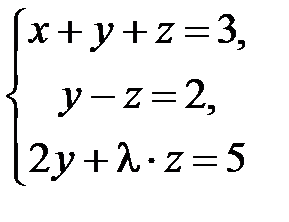 не имеет решений, если
не имеет решений, если 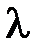 равно …
равно …
-: 2
-: -5
+: -2
-: 5
I:
S: Система линейных уравнений  не имеет решений, если
не имеет решений, если  равно …
равно …
-: 6
-: -3
+: -6
-: 3
I:
S: Если 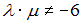 , то решение системы линейных уравнений
, то решение системы линейных уравнений 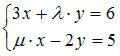 методом Крамера можно представить в виде …
методом Крамера можно представить в виде …
+: 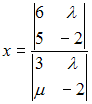 ,
, 
-:  ,
, 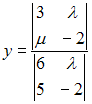
-: 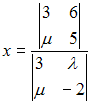 ,
, 
-: 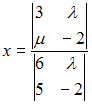 ,
, 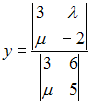
I:
S: Дана система уравнений 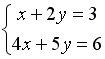 . Для того, чтобы найти значение переменной y при решении этой системы по формулам Крамера, достаточно вычислить только определители…
. Для того, чтобы найти значение переменной y при решении этой системы по формулам Крамера, достаточно вычислить только определители…
+: 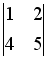 и
и 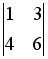
-:  и
и 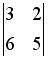
-:  и
и 
-:  ,
,  и
и 
I:
S: Дана система уравнений  . Для того, чтобы найти значение переменной y при решении этой системы по формулам Крамера, достаточно вычислить только определители…
. Для того, чтобы найти значение переменной y при решении этой системы по формулам Крамера, достаточно вычислить только определители…
-:  ,
,  и
и 
+:  и
и 
-:  и
и 
-:  и
и 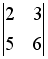
I:
S: Система линейных уравнений 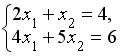 решается по правилу Крамера. Установите соответствие между определителями системы и их значениями.
решается по правилу Крамера. Установите соответствие между определителями системы и их значениями.
L1: 
L2: 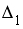
L3: 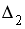
R1: 6
R2: 14
R3: – 4
R4: 2
I:
S: Система линейных уравнений 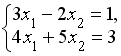 решается по правилу Крамера. Установите соответствие между определителями системы и их значениями.
решается по правилу Крамера. Установите соответствие между определителями системы и их значениями.
L1: 
L2: 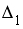
L3: 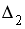
R1: 23
R2: 11
R3: 5
R4: – 5
I:
S: Система линейных уравнений 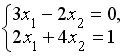 решается по правилу Крамера. Установите соответствие между определителями системы и их значениями.
решается по правилу Крамера. Установите соответствие между определителями системы и их значениями.
L1: 
L2: 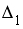
L3: 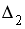
R1: 16
R2: 2
R3: 3
R4: – 3
I:
S: Система линейных уравнений 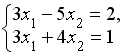 решается по правилу Крамера. Установите соответствие между определителями системы и их значениями.
решается по правилу Крамера. Установите соответствие между определителями системы и их значениями.
L1: 
L2: 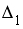
L3: 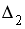
R1: 27
R2: 13
R3: – 3
R4: 3
I:
S: Система линейных уравнений  решается по правилу Крамера. Установите соответствие между определителями системы и их значениями.
решается по правилу Крамера. Установите соответствие между определителями системы и их значениями.
L1: 
L2: 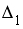
L3: 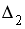
R1: – 1
R2: 7
R3: 6
R4: – 6
I:
S: Укажите систему линейных уравнений, подготовленную для обратного хода метода Гаусса.
-: 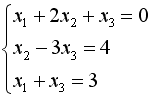
-: 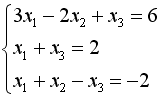
-: 
+: 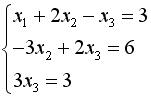
I:
S: Укажите систему линейных уравнений, подготовленную для обратного хода метода Гаусса.
-: 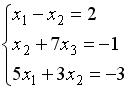
+: 
-: 
-: 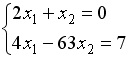
I:
S: Укажите систему линейных уравнений, подготовленную для обратного хода метода Гаусса.
-: 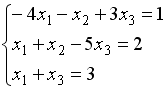
-: 
+: 
-: 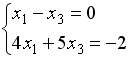
I:
S: Установите соответствие между системой линейных уравнений и ее расширенной матрицей.
L1: 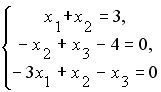
L2: 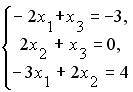
L3: 
L4: 
R1: 
R2: 
R3: 
R4: 
R5: 
R6: 
I:
S: Установите соответствие между системой линейных уравнений и ее расширенной матрицей.
L1: 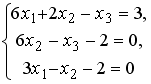
L2: 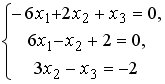
L3: 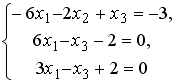
L4: 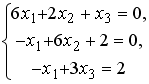
R1: 
R2: 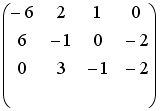
R3: 
R4: 
R5: 
R6: 
I:
S: Установите соответствие между системой линейных уравнений и ее расширенной матрицей.
L1: 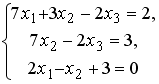
L2: 
L3: 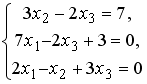
L4: 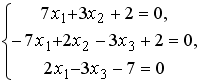
R1: 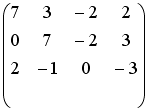
R2: 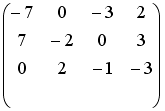
R3: 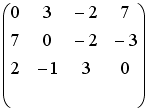
R4: 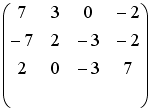
R5: 
R6: 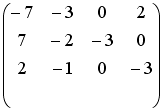
I:
S: Установите соответствие между системой линейных уравнений и ее расширенной матрицей.
L1: 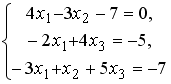
L2: 
L3: 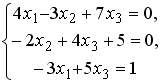
L4: 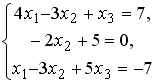
R1: 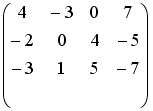
R2: 
R3: 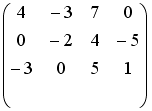
R4: 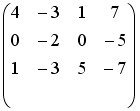
R5: 
R6: 
V2: Векторная алгебра
I:
S: Известны координаты точек 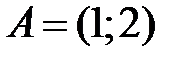 и
и  . Если
. Если 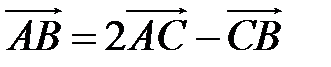 , то координаты точки
, то координаты точки 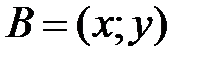 равны …
равны …
-: 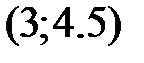
+: 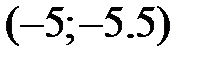
-: 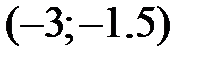
-: 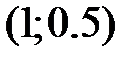
I:
S: Даны векторы 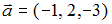 и
и 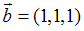 ; если
; если 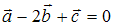 , то вектор
, то вектор 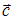 равен …
равен …
-: 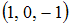
-: 
+: 
-: 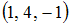
I:
S: Если известны координаты вершин 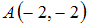 ,
,  ,
,  треугольника ABC, то вектор
треугольника ABC, то вектор 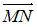 , где М и N – середины сторон АВ и ВС соответственно, равен …
, где М и N – середины сторон АВ и ВС соответственно, равен …
+: 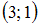
-: 
-: 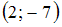
-: 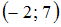
I:
S: Даны векторы  . Тогда линейная комбинация
. Тогда линейная комбинация 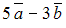 этих векторов равна …
этих векторов равна …
-: 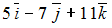
-: 
+: 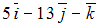
-: 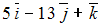
I:
S: Направляющим для прямой, заданной уравнением 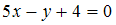 , будет вектор …
, будет вектор …
-: 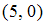
-: 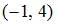
+: 
-: 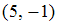
I:
S: Если 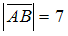 ,
,  ,
,  и точки A, B, C являются вершинами треугольника, то скалярное произведение векторов
и точки A, B, C являются вершинами треугольника, то скалярное произведение векторов 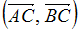 равно …
равно …
-: 9
+: 4
-: 14
-: 20
I:
S: Даны векторы 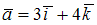 и
и 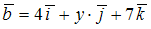 , где
, где 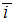 ,
, 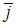 и
и 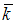 – ортонормированный базис. Известно, что скалярное произведение этих векторов равно 40, а угол между этими векторами равен
– ортонормированный базис. Известно, что скалярное произведение этих векторов равно 40, а угол между этими векторами равен  . Тогда значение
. Тогда значение 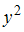 равно …
равно …
-: 35
-: 68.2
+: 191
-: 0
I:
S: Площадь треугольника, образованного векторами  и
и 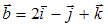 , равна …
, равна …
-: 
-: 
+: 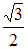
-: 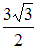
I:
S: Направляющий вектор прямой, заданной как пересечение двух плоскостей  , равен …
, равен …
-: 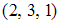
-: 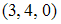
-: 
+: 
I:
S: Длина стороны квадрата, площадь которого равна площади параллелограмма, построенного на векторах  и
и  , равна …
, равна …
-: 1
-: 
+: 
-: 3
I:
S: Векторное произведение векторов  и
и 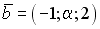 равно нулю, если…
равно нулю, если…
-: 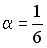 ;
; 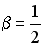
+: 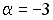 ;
; 
-: 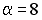 ;
; 
-: 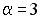 ;
; 
I:
S: Векторное произведение векторов 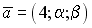 и
и 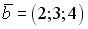 равно нулю, если…
равно нулю, если…
-:  ;
; 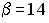
-: 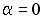 ;
; 
-: 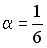 ;
; 
+: 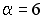 ;
; 
I:
S: Векторное произведение векторов  и
и 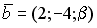 равно нулю, если…
равно нулю, если…
-: 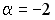 ;
; 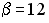
-: 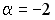 ;
; 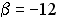
+: 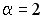 ;
; 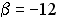
-: 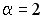 ;
; 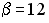
I:
S: Векторное произведение векторов 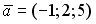 и
и 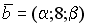 равно нулю, если…
равно нулю, если…
-:  ;
; 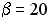
+: 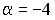 ;
; 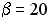
-: 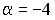 ;
; 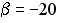
-:  ;
; 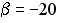
I:
S: Векторное произведение векторов  и
и  равно нулю, если…
равно нулю, если…
-: 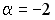 ;
; 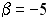
+: 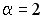 ;
; 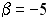
-: 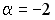 ;
; 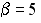
-: 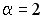 ;
;