Прогноз значения зависимость средней температуры прогрева частицы от её радиуса для наполнителя NH4Cl.с помощью функции наиболее хорошо аппроксимирующей табличные данные, т.е по формуле (23).Результаты вычислений прогнозного значения представлены на рис.13.
| ПРОГНОЗНОЕ ЗНАЧЕНИЕ | ||
| Xmax= | 3,00 | |
| Xmin= | 1,20 | |
| R= | 1,80 | |
| x= | 0,7823077 | |
| y= | 1,94 |
Рис.13.Фрагмент рабочего листа MS Excel вычисления прогнозного значения.
Здесь в ячейку H29 введена формула
=МАКС(B3:B16)
В ячейку H30 введена формула =МИН(B3:B16)
В ячейку H31 введена формула=H29-H30
В ячейку H32 введена формула=A19+0,1*H31
В ячейку H33 введена формула=E26+E27*H32
8.Расчёт аппроксимаций по программе в среде TURBO PASCAL 7.0

Program Kurs_MNK;
Uses crt,Graph;
Const
Nmax=100;
Type
Vector=array[1..Nmax] of real;
ari=array[1..100] of longint;
Var
f,g: text;
filevvod:string;
x1,y1:ari;
x,y,lny,STL,SsrL,STsqr,Ssrsqr: Vector;
Ftab,Stab:vector;
YL,Ysqr,Yexp,lnYexp:Vector;
i,N,N1: integer;
Sx,Sy,Sxy,Sx2,Sx3,Sx4,Sx2y,Sx2sr,Sy2sr,Sxysr,Slny,Sxlny:real;
a1L,a2L,koef_cor:real;
MD:real;
Sa1L,Sa2L:real;
Xsr,Ysr,lnYsr:real;
SostL,SregrL,SpolnL,R_det_L:real;
FLine,SLine,ta1L,ta2L:real;
a1sqr,a2sqr,a3sqr:real;
Sa1sqr,Sa2sqr,Sa3sqr:real;
Sostsqr,Sregrsqr,Spolnsqr,R_det_sqr,DSost:real;
Fsqr,Ssqr,ta1sqr,ta2sqr,ta3sqr:real;
cexp,a1exp,a2exp:real;
Sa1exp,Sa2exp:real;
Sostexp,Sregrexp,Spolnexp,R_det_exp:real;
Fexp,ta1exp,ta2exp:real;
gr:integer;
Min,Max,Xpr,Ypr:real;
Procedure Inp_vect(name:String;Var a,b:Vector; Var N:Integer);
Var
k:integer;
f:text;
Begin
N:=0;
k:=1;
Assign(f,name);
{$I-}
reset(f);
{$I+}
if IOResult = 0 then
begin
reset(f);
while not SeekEOF(f) do
begin
while not SeekEOLN(f) do
begin
ReadLn(f,a[k],b[k]);
N:=N+1;
k:=k+1;
end;
end;
close(f);
end
else WriteLn('File with name ',name,' not found');
end;
Procedure L_Kram(Var a11:Integer; Var a12,a21,a22,b1,b2:real; Var a1,a2:real);
Var
D,D1,D2: Real;
begin
D:=a11*a22-a21*a12;
D1:=b1*a22-b2*a12;
D2:=a11*b2-a21*b1;
a1:=D1/D;
a2:=D2/D;
end;
Procedure Sqr_Kram(var a11:integer;
var a12,a13,a21,a22,a23,a31,a32,a33,b1,b2,b3:real;
var a1,a2,a3,MD:real);
var
D,D1,D2,D3:real;
begin
D:=a11*a22*a33+a12*a23*a31+a21*a32*a13-a13*a22*a31-a21*a12*a33-a11*a23*a32;
D1:=b1*a22*a33+a12*a23*b3+b2*a32*a13-a13*a22*b3-b2*a12*a33-b1*a23*a32;
D2:=a11*b2*a33+b1*a23*a31+a21*b3*a13-a13*b2*a31-a21*b1*a33-a11*a23*b3;
D3:=a11*a22*b3+a12*b2*a31+a21*a32*b1-b1*a22*a31-a21*a12*b3-a11*b2*a32;
a1:=D1/D;
a2:=D2/D;
a3:=D3/D;
MD:=D;
end;
Procedure koef_det(ns:integer;a,b:vector;c:real;var s1,s2,s3,r:real);
var
i:integer;
begin
for i:=1 to ns do
begin
s1:=s1+sqr(b[i]-a[i]);
s2:=s2+sqr(b[i]-c);
end;
s3:=s1+s2;
R:=1-s1/s3;
end;
Procedure ZnachLine(n:integer; DS,R2,a,asr,a1,a2:real; var s1,s2,f,t1,t2:real);
begin
s1:=sqrt(ds*a/(n*(n-2)*asr));
s2:=sqrt(ds/((n-2)*asr));
f:=R2*(n-2)/(1-R2);
t1:=abs(a1)/s1;
t2:=abs(a2)/s2;
end;
Procedure print(var gr:integer;
sa1,sa2,sa3,sk,sR,sm1,sm2,sm3,sf,st1,st2,st3:string;
a1,a2,a3,k,R,m1,m2,m3,f,t1,t2,t3:real);
var
Fd,Sd:real;
st:string;
begin
Case gr of
1: st:='Linear approximation';
2: st:='Quadratic approximation';
3: st:='Exponentional approximation';
end;
write(g,sa1,'=',a1:7:4,' ',sa2,'=',a2:7:4);
if gr=2 then write(g,' ',sa3,'=',a3:7:4);
writeln(g,' - coefficients ',st);
if gr=1 then writeln(g,sk,k:9:6,' - correlation coefficients');
writeln(f,sr,r:9:6,' - determination coefficient');
write(g,sm1,m1:8:6,' ',sm2,m2:8:6);
if gr=2 then write(g,' ',sm3,m3:8:6);
writeln(g,' - standard errors of coefficients');
writeln(g,'Criteria for checking null hypotheses');
write(g,sf,f:8:3,' ',st1,t1:8:3,' ',st2,t2:8:3);
if gr=2 then write(g,' ',st3,t3:8:3);
writeln(g);
if gr=2 then fd:=ftab[2] else fd:=ftab[1];
if gr=2 then sd:=stab[2] else sd:=stab[1];
if f>fd then writeln(g,'equation ',st,' is significant')
else writeln(g,'equation ',st,' is not significant');
if t1>sd then writeln(g,'coefficient ',sa1,' is significant')
else writeln(g,'coefficient ',sa1,' is not significant');
if t2>sd then writeln(g,'coefficient ',sa2,' is significant')
else writeln(g,'coefficient ',sa2,' is not significant');
if gr=2 then
if t3>sd then writeln(g,'coefficient ',sa3,' is significant')
else writeln(g,'coefficient ',sa3,' is not significant');
end;
Procedure grafik(var gr:integer);
const
k=100;
kxn=95;kxk=590;
kyn=70;kyk=385;
var
dr,md,i:integer;
x,y:vector;
kx,ky:ari;
ymin,ymax:real;
l:integer;
vol:string;
mx,my:real;
h:real;
function IntStr(l,dig:integer):string;
var buf:string[10];
begin
str(l:dig,buf);
IntStr:=buf;
end;
begin
clrscr;
h:=30/(k-1);
x[1]:=0;
ymin:=0;
ymax:=100;
for i:=1 to k do
begin
case gr of
1: y[i]:=a1l+a2l+x[i];
2: y[i]:=a1sqr+a2sqr+x[i]+a3sqr*x[i]*x[i];
3: y[i]:=a1exp*exp(a2exp*x[i]);
end;
if i<>100 then x[i+1]:=x[i]+h;
end;
mx:=(kxk-kxn)/(x[k]-x[1]);
my:=(kyk-kyn)/(ymax-ymin);
for i:=1 to k do
begin
kx[i]:=round((x[i]-x[1])*mx)+kxn;
ky[i]:=round((ymax-y[i])*my)+kyn;
end;
dr:=detect;
initgraph(dr,md,'');
setbkcolor(7);
cleardevice;
setcolor(1);
setlinestyle(0,0,2);
line(95,385,590,385);
line(95,385,95,70);
settextstyle(1,0,2);
for i:=0 to 10 do
begin
l:=100-i*10;
vol:=intstr(l,3);
outtextxy(30,50+i*32,vol);
end;
for i:=0 to 6 do
begin
l:=0+i*5;
vol:=intstr(l,3);
outtextxy(70+i*85,390,vol);
end;
for i:=1 to n do
circle(x1[i],y1[i],2);
case gr of
1: outtextxy(250,70,'y = a1L + a2L * x');
2: outtextxy(180,70,'y = a1sqr + a2sqr * x + a3sqr * x^2');
3: outtextxy(220,70,'y = a1exp * exp(a2exp * x)');
end;
setcolor(4);
for i:=1 to k-1 do
line(kx[i],ky[i],kx[i+1],ky[i+1]);
readkey;
closegraph;
end;
procedure minmax(var a:vector;var n:integer; var min,max:real);
var i:integer;
begin
min:=a[1];
max:=a[1];
for i:=2 to n do
begin
if a[i]<min then min:=a[i];
if a[i]>max then max:=a[i];
end;
end;
BEGIN
writeln('Enter full name of the source data file');
readln(filevvod);
inp_vect(filevvod,x,y,n);
writeln('Enter full name of the table data file');
readln(filevvod);
inp_vect(filevvod,ftab,stab,n1);
sx:=0; sy:=0; sx2:=0; sxy:=0;
sx3:=0; sx4:=0; sx2y:=0;
slny:=0; sxlny:=0;
for i:=1 to n do
begin
sx:=sx+x[i];
sy:=sy+y[i];
sx2:=sx2+sqr(x[i]);
sxy:=sxy+x[i]*y[i];
sx3:=sx3+sqr(x[i])*x[i];
sx4:=sx4+sqr(sqr(x[i]));
sx2y:=sx2y+sqr(x[i])*y[i];
lny[i]:=ln(y[i]);
slny:=slny+lny[i];
sxlny:=sxlny+x[i]*lny[i];
end;
xsr:=sx/n;
ysr:=sy/n;
lnysr:=slny/n;
sxysr:=0; sx2sr:=0; sy2sr:=0;
for i:=1 to n do
begin
sxysr:=sxysr+(x[i]-xsr)*(y[i]-ysr);
sx2sr:=sx2sr+sqr(x[i]-xsr);
sy2sr:=sy2sr+sqr(y[i]-ysr);
end;
l_kram(n,sx,sx,sx2,sy,sxy,a1l,a2l);
koef_cor:=sxysr/(sqrt(sx2sr)*sqrt(sy2sr));
for i:=1 to n do yl[i]:=a1l+a2l*x[i];
koef_det(n,y,yl,ysr,sostl,sregrl,spolnl,r_det_l);
znachline(n,sostl,r_det_l,sx2,sx2sr,a1l,a2l,sa1l,sa2l,fline,ta1l,ta2l);
sqr_kram(n,sx,sx2,sx,sx2,sx3,sx2,sx3,sx4,sy,sxy,sx2y,a1sqr,a2sqr,a3sqr,md);
for i:=1 to n do ysqr[i]:=a1sqr+a2sqr*x[i]+a3sqr*sqr(x[i]);
koef_det(n,y,ysqr,ysr,sostsqr,sregrsqr,spolnsqr,r_det_sqr);
dsost:=sostsqr/(n-3);
sa1sqr:=sqrt(dsost*(sx2*sx4-sx3*sx3)/md);
sa2sqr:=sqrt(dsost*(n*sx4-sx2*sx2)/md);
sa3sqr:=sqrt(dsost*(n*sx2-sx*sx)/md);
fsqr:=r_det_sqr*(n-3)/(2*(1-r_det_sqr));
ta1sqr:=abs(a1sqr)/sa1sqr;
ta2sqr:=abs(a2sqr)/sa2sqr;
ta3sqr:=abs(a3sqr)/sa3sqr;
l_kram(n,sx,sx,sx2,slny,sxlny,cexp,a2exp);
a1exp:=exp(cexp);
for i:=1 to n do
begin
yexp[i]:=a1exp*exp(a2exp*x[i]);
lnyexp[i]:=ln(yexp[i]);
end;
koef_det(n,lny,lnyexp,lnysr,sostexp,sregrexp,spolnexp,r_det_exp);
znachline(n,sostexp,r_det_exp,sx2,sx2sr,a1exp,a2exp,sa1exp,sa2exp,fexp,ta1exp,ta2exp);
assign(g,'out.dat');
rewrite(g);
writeln(g,'Source data');
for i:=1 to n do writeln(g,x[i]:6:2,' ',y[i]:6:2);
writeln(g,' N=',N:2,' - number of observations');
writeln(g,'Table data');
for i:=1 to n1 do writeln(g,ftab[i]:6:2,' ',stab[i]:8:4);
gr:=1;
print(gr,'a1L','a2L','','koef_cor=','R_det_L=','Sa1L=','Sa2L=','',
' FLine=','ta1L=','ta2L=','',a1L,a2L,0,koef_cor,r_det_l,
sa1l,sa2l,0,fline,ta1l,ta2l,0);
gr:=2;
print(gr,'a1sqr','a2sqr','a3sqr','','R_det_sqr=',' Sa1sqr=',' Sa2sqr=',
' Sa3sqr=','Fsqr=','ta1sqr=','ta2sqr=','ta3sqr=',a1sqr,a2sqr,
a3sqr,0,r_det_sqr,sa1sqr,sa2sqr,sa3sqr,fsqr,ta1sqr,ta2sqr,ta3sqr);
gr:=3;
print(gr,' a1exp',' a2exp','','',' R_det_exp=',' Sa1exp=',' Sa2exp=','',
' Fexp=','ta1exp=','ta2exp=','',a1exp,a2exp,0,0,r_det_exp,
sa1exp,sa2exp,0,fexp,ta1exp,ta2exp,0);
minmax(x,n,min,max);
xpr:=xsr+0.1*(max-min);
ypr:=a1l+a2l*xpr;
writeln(g,'In the forecast point Xpr=',xpr:6:4,' forecast value Ypr=',ypr:6:4);
close(g);
for i:=1 to n do
begin
x1[i]:=round(95+x[i]*495/30);
y1[i]:=round(385-y[i]*315/100);
end;
gr:=1;
grafik(gr);
gr:=2;
grafik(gr);
gr:=3;
grafik(gr);
END.
((((((В результате программы был создан файл out.txt.
Его содержимое таково:
Source data
0.30 12.00
0.34 18.00
0.40 25.00
0.41 32.00
0.42 38.00
0.43 44.00
0.45 50.00
0.46 56.00
0.47 62.00
0.48 68.00
0.49 75.00
0.43 82.00
0.45 87.00
0.32 100.00
N=14 - number of observations
Table data
4.75 2.1604
4.84 2.1788
a1L=-18.9299 a2L=173.3365 - coefficients Linear approximation
koef_cor= 0.381798 - correlation coefficients
Sa1L=51.087560 Sa2L=121.130453 - standard errors of coefficients
Criteria for checking null hypotheses
FLine= 2.048 ta1L= 0.371 ta2L= 1.431
equation Linear approximation is not significant
coefficient a1L is not significant
coefficient a2L is not significant
a1sqr=277.9180 a2sqr=-1369.9111 a3sqr=1956.4418 - coefficients Quadratic approximation
Sa1sqr=359.837834 Sa2sqr=1855.333517 Sa3sqr=2346.937491 - standard errors of coefficients
Criteria for checking null hypotheses
Fsqr= 1.345 ta1sqr= 0.772 ta2sqr= 0.738 ta3sqr= 0.834
equation Quadratic approximation is not significant
coefficient a1sqr is not significant
coefficient a2sqr is not significant
coefficient a3sqr is not significant
a1exp= 3.5136 a2exp= 6.1484 - coefficients Exponentional approximation
Sa1exp=1.043173 Sa2exp=2.473400 - standard errors of coefficients
Criteria for checking null hypotheses
Fexp= 6.179 ta1exp= 3.368 ta2exp= 2.486
equation Exponentional approximation is significant
coefficient a1exp is significant
coefficient a2exp is significant
In the forecast point Xpr=0.4369 forecast value Ypr=56.7934)))))) ИСПРАВИТЬ
Вывод.
В курсовой работе мы решили задачу при проведении эксперимента зависимости средней температуры прогрева частицы от её радиуса для различных наполнителей. зависимость средней температуры прогрева частицы от её радиуса для различных наполнителей, определили тип и параметры аналитической зависимости, аппроксимирующей результаты испытаний. Используя компьютерные возможности, которые мы проходили на первом курсе нашего обучения в СПГГУ, и методические указания. Это во многом облегчило нам решение поставленной задачи. Курсовая выполнена и оформлена программами: текстовой редактор Microsoft World, электронные таблицы Microsoft Excel. Программа на языке программирования Паскаль является реализацией цикла табулирования. Полученные ответы выполненные разными программами, сходятся и проверены.
Список литературы.
1. Методические указания по выполнению курсовой работы / Санкт Петербургский государственный горный институт (технический университет). Сост. Г.Н.Журов, В.В.Беляев, Г.П.Парамонов. СПб,2010.54 с.
2.Беляев В.В. Информатика. Аппроксимация методом наименьших квадратов. Методическое указание по выполнению курсовой работы студентов всех специальностей. / В.В. Беляев, Г.Н. Журов. Спб.:СПГГИ(ТУ),2005.
Приложения
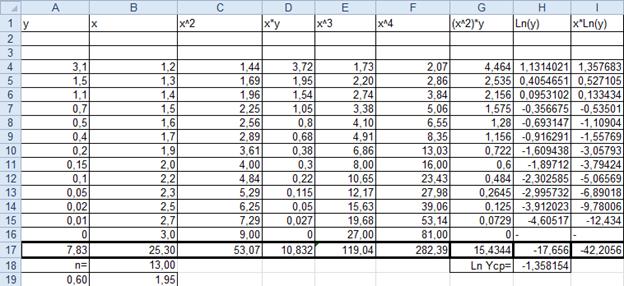
Рис.15. Образ в программе Microsoft Excel.

Рис.16. Образ в программе Microsoft Excel.
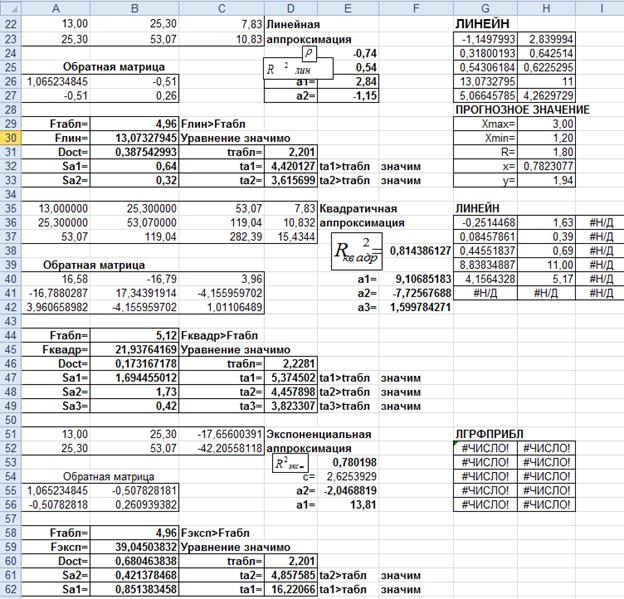
Рис.17. Образ в программе Microsoft Excel.


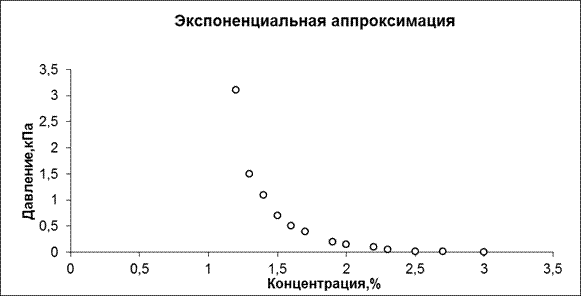
Рис.18. Образ в программе Microsoft Excel (графики).






