Дать определение матрицы. Перечислить основные виды матриц.
Определение: Таблица чисел, содержащая m строк и n столбцов, называется матрицей размерностью m×n ( 
)
Виды матриц:
1. Матрица-строка (строковая) - матрица размерностью 
2. Матрица-столбец - матрица размерностью 
3. Квадратная матрица - количество строк равно количеству столбцов (m=n). У квадратной матрицы существует две диагонали: главная диагональ (a11, a22,..., ann) и побочная диагональ (a1n, a2n-1,..., an1).
4. Нулевая матрица (0) - матрица, состоящая из одних нулей. В матричной алгебре играет роль 0.
5. Диагональная матрица - квадратная матрица, все элементы которой, кроме главной диагонали, равны нулю.
6. Скалярная матрица - диагональная матрица, все элементы главной диагонали которой равны между собой.
7. Единичная матрица (E) - скалярная матрица, все элементы главной диагонали которой равны 1.
Вопрос 2.
Перечислить основные операции над матрицами и их свойства.
1. Умножение матрицы на число: произведение матрицы A на число λ называется матрица C размерностью равной A, элементы которой равны произведению числа λ на соответствующий элемент матрицы A.
2. Сложение матриц: суммой матриц и 
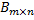называется матрица 
, элементы которой равны сумме соответствующих элементов матриц A и B. Обязательное условие: две матрицы одной размерности.
3. Разность матриц определяется аналогично
4. Умножение матриц: произведением матрицы и матрицы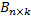 
называется матрица 
, элементы которой равны сумме произведений соответствующих элементов строки матрицы A на соответствующие элементы столбца матрицы B.
5. Операция транспонирования: транспонированной матрицей AT к матрице называется матрица размерностью n×m, строки которой являются соответствующими столбцами матрицы A.
Свойства операций:
1) A+B=B+A (коммутативность)
2) (A+B)+C=A+(B+C) (ассоциативность)
3) (A×B)×C=A×(B×C) (ассоциативность)
4) A×(B+C)=A×B+A×C (дистрибутивность)
5) A+0=A
6) A-квадратная матрица, A×E=E×A=A
Вопрос 3.
Дать определение определителя матрицы и перечислить его свойства.
Определителем произвольной квадратной матрицы A n-ого(detA) порядка называется число, вычисляемое по следующему правилу: (разложение определителя матрицы A по первой строке)
;
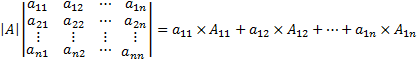где A11, A12, A1n - алгебраические дополнения(число, вычисляемое по формуле 
)
Минором (Mij) элемента aij матрицы A называется определитель матрицы, получаемый вычеркиванием в матрице A i-ой строки и j-ого столбца.
Свойства определителя:
1. |A| = |AT|
Замечание: благодаря свойству 1 все свойства определителя строк можно переносить на столбцы.
2. Разложение определителя матрицы А можно провести по любой строке.
3. Если в исходной матрице поменять местами две строки, то определитель матрицы поменяет знак на противоположный.
4. Определитель матрицы, полученной прибавлением к какой-либо строке другой строки, умноженной на какое либо число, равен исходной матрице.
5. Определитель матрицы, содержащий одинаковые строки, равен нулю.
6. Если матрица содержит линейно зависимые строки, то её определитель равен нулю.
7. Если хотя бы одна строка матрицы нулевая, то определитель равен нулю.
8. Определитель произведения квадратных матриц одинакового порядка равен произведению их определителей (|A×B| = |A|×|B|)
9. 
Вопрос 4.
