Геометрический смысл модуля
Модуль числа — это расстояние от нуля до данного числа.
Например, |-5| = 5. То есть расстояние от точки -5 до нуля равно 5.

Рассмотрим простейшее уравнение |x| = 3. Мы видим, что на числовой прямой есть две точки, расстояние от которых до нуля равно трём. Это точки 3 и -3. Значит, у уравнения |x| = 3 есть два решения: x = 3 и x = -3.
Пример 1.
|x — 3| = 4.
Это уравнение можно прочитать так: расстояние от точки  до точки
до точки 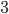 равно
равно  . С помощью графического метода можно определить, что уравнение имеет два решения:
. С помощью графического метода можно определить, что уравнение имеет два решения:  и
и  .
.

Пример 2.
Решим неравенство: |x + 7| < 4.
Можно прочитать как: расстояние от точки  до точки
до точки  меньше четырёх. Ответ: (-11; -3).
меньше четырёх. Ответ: (-11; -3).

Пример 3.
Решим неравенство: |10 — x| ≥ 7.
Расстояние от точки 10 до точки  больше или равно семи. Ответ: (-∞; 3]υ [17, +∞)
больше или равно семи. Ответ: (-∞; 3]υ [17, +∞)

График функции y = |x|
Для x≥ 0 имеем y = x. Для x < 0 имеем y = -x.

Решение уравнений и неравенств, содержащих модуль числа
При решении задач, содержаних модуль вещественного числа, основным приемом является раскрытие знака модуля в соответствии с его свойствами.
Таким образом, если под знаком модуля стоит выражение, зависящее от переменной, мы раскрываем модуль по определению:

В некоторых случаях модуль раскрывается однозначно. Например:  , так как выражение под знаком модуля неотрицательно при любых
, так как выражение под знаком модуля неотрицательно при любых  и
и  . Или
. Или  , так как выражением под модулем не положительно при любых
, так как выражением под модулем не положительно при любых  .
.
Билет№7: Алгоритм освобождения от знака модуля.
1. Прировнять выражения стоящих под знаком, т. е. найти нули модуля, решив полученные уравнения.
2. Расположить в порядке возрастания нули модулей на числовой прямой, которые разобьют ее на интервалы.
3. Определить знак выражения, стоящего под знаком модуля в каждом интнрвале.
4. Если выражение под знаком модуля положительное, то убирая модуль, знак, стоящий перед выражением, необходимо сохранить. Если выражение отрицатольное, то убирая модуль, необходимо знак, стоящий перед выражением, изменить на противоположный.
Билет№8: Методы решения уравнений (неравенств) содержащих знак модуля.
1. Метод возведения обоих частей уравнения в квадрат. Этот метод применяется в том случае если обе части уравнения положительные при любых значениях, например |x+2|=3.
2. Универсальный метод заключается в том, что необходимо найти нули модуля и отметить на координатной прямой полученные точки. Определить знак модуля в каждом интервале, решить уравнения в каждом интервале.
Билет№9: Решение неравенств методом интнрвалов.
План решения неравенства методом интервалов.
Переносим все члены неравенства в одну сторону (например, влево)
Не производя абсолютно никаких преобразований, находим область определения функции стоящей в левой части неравенства, после чего в области определения функции с целью упрощения допускается выполнение тождественных преобразований.
Находим нули функций.
Рисуем пунктиром числовую ось, после чего сплошной линией обводим промежутки оси, принадлежащие области определения функции. На них точки, в которых функция терпит разрыв, отмечаем “пустыми” (не заштрихованными), отмечаем на оси нули (корни) функции:
- “пустыми” (не заштрихованными), точками, если неравенство строгое полными (черными), заштрихованными точками, если неравенство не строгое.
Определяем знак функции на каждом из полученных интервалов (например,
подстановкой в выражении функции какого-либо значения из соответствующего интервала).
выбираем для ответа нужные интервалы в соответствии со знаком неравенства.
Записываем ответ.
Билет№10: Функция y=sinx. График, свойства.
y = sin x

график - синусоида
Свойства функции
- Область определения: R
- Область значений: [-1; 1]
- Четность, нечетность: функция нечетная
- Нули: sin x = 0 при x = πn, n
 Z
Z - Промежутки знакопостоянства:
sin x > 0 при x (2 π n; n + 2 π n), n
(2 π n; n + 2 π n), n  Z
Z
sin x < 0 при x (- π + 2 π n; 2 π n), n
(- π + 2 π n; 2 π n), n  Z
Z - Экстремумы:
xmin = + 2 π n, n Z; ymin = -1
Z; ymin = -1
xmax = + 2 π n, n Z; ymin = 1
Z; ymin = 1 - Промежутки монотонности:


- Функция переодическая с наименьшим положительным периудом 2 π
Билет№11: Функция y=cosx. График, свойства.
y = cos x

график - косинусоида
Свойства функции
- Область определения: R
- Область значений: [-1; 1]
- Четность, нечетность: функция четная
- Период: 2

- Нули:

- Промежутки знакопостоянства:
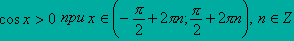

- Экстремумы:
x min = + 2
+ 2  n, n
n, n  Z; ymin = -1
Z; ymin = -1
x max = 2 n, n
n, n  Z; ymin = 1
Z; ymin = 1 - Промежутки монотонности:

 < LI>
< LI>
Преобразования графиков y = sinx и y = cosx:
Графики функций y = sinx и y = cosx можно получить друг из друга путем параллельных переносов
вдоль оси x на  /2:
/2:

<>
Билет№12: Функция y=tgx. График, свойства.
y = tg x

график - тангенсоида
Свойства функции
- Область определения: объединение интервалов

- Область значений: R
- Четность, нечетность: функция нечетная
- Период:

- Нули: y = 0 при x =
 n, n
n, n  Z
Z - Промежутки знакопостоянства:


- Экстремумов нет
- Промежутки монотонности:
функция возрастает на каждом интервале области определения - Асимптоты: x =
 +
+  n, n
n, n  Z
Z
Билет№13: Функция y=сtgx. График, свойства.
y = ctg x

график - катангенсоида
Свойства функции
- Область определения: объединение интервалов

- Область значений: R
- Четность, нечетность: функция нечетная
- Период:

- Нули:

- Промежутки знакопостоянства:


- Экстремумов нет
- Промежутки монотонности:
функция убывает на каждом интервале области определения - Асимптоты: x =
 n, n
n, n  Z
Z
Преобразования графика y = ctgx:
График функци y = ctgx получается из графика у =tgx путем отражения относ. любой из координатныхосей и последующим параллельным переносом вдоль оси x на  /2.
/2.
Билет№14: Определение тригонометрических функций по окружности и по треугольнику.
Синус угла — отношение противолежащего катета к гипотенузе:  Это отношение не зависит от выбора треугольника ABC, содержащего угол α, так как все такие треугольники подобны.
Это отношение не зависит от выбора треугольника ABC, содержащего угол α, так как все такие треугольники подобны.
 Косинус угла — отношение прилежащего катета к гипотенузе:
Косинус угла — отношение прилежащего катета к гипотенузе:  Так как
Так как 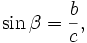 синус одного острого угла в треугольнике равна косинусу второго, и наоборот.
синус одного острого угла в треугольнике равна косинусу второго, и наоборот.
 Тангенс угла — отношение противолежащего катета к прилежащему:
Тангенс угла — отношение противолежащего катета к прилежащему: 
 Котангенс угла — отношение прилежащего катета к противолежащему:
Котангенс угла — отношение прилежащего катета к противолежащему: 
По окружности:
Так как длина отрезка OA равна 1, то 
 Косинусом угла
Косинусом угла  называется отношение абсциссы точки A к длине отрезка OA. Обозначают
называется отношение абсциссы точки A к длине отрезка OA. Обозначают  Так как длина отрезка OA равна 1, то
Так как длина отрезка OA равна 1, то 
 Тангенсом угла
Тангенсом угла  называется отношение ординаты точки A к абсциссе точки A. Обозначают
называется отношение ординаты точки A к абсциссе точки A. Обозначают  (в англоязычной литературе
(в англоязычной литературе  Так как
Так как  и
и  то
то 
 Котангенсом угла
Котангенсом угла  называется отношение абсциссы точки A к ординате точки A. Обозначают
называется отношение абсциссы точки A к ординате точки A. Обозначают  Так как
Так как  и
и  то
то 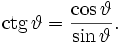 Котангенс равен обратному значению тангенса.
Котангенс равен обратному значению тангенса. 
Билет №15: y=arccos, y=arcsin определение, свойства.
1.Функция y = arcsin х.
Арксинусом числа m называется такое значение угла x, для которого 
Функция y = sin x непрерывна и ограничена на всей своей числовой прямой. Функция y = arcsinx является строго возрастающей.
-
 при
при 
-
 при
при 
-
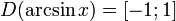 (область определения),
(область определения), -
 (область значений).
(область значений).
Свойства функции arcsin:
-
 (функция является нечётной).
(функция является нечётной). -
 при
при  .
. -
 при x = 0.
при x = 0. -
 при
при 
-

-
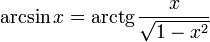

Получение функции arcsin
Дана функция y = sin x. На всей своей области определения она является кусочно-монотонной, и, значит, обратное соответствие y = arcsinx функцией не является. Поэтому мы рассмотрим отрезок, на котором она строго возрастает и принимает все значения области значений — 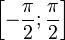 . Так как для функции y = sin x на интервале
. Так как для функции y = sin x на интервале 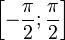 каждому значению аргумента соответствует единственное значение функции, то на этом отрезке существует обратная функция y = arcsin x, график которой симметричен графику функции y = sin x на отрезке
каждому значению аргумента соответствует единственное значение функции, то на этом отрезке существует обратная функция y = arcsin x, график которой симметричен графику функции y = sin x на отрезке 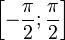 относительно прямой y = x.
относительно прямой y = x.
Арккосинусом числа m называется такое значение угла x, для которого 
Функция y = cos x непрерывна и на всей своей числовой прямой. Функция y = arccos x является строго убывающей.
- cos(arccos x) = x при

- arccos(cos y) = y при

- D(arccos x) = [ − 1;1], (область определения),
- E(arccos x) = [0;π]. (область значений).
Свойства функции arccos
-
 (функция центрально-симметрична относительно точки
(функция центрально-симметрична относительно точки 
-
 при
при 
-
 при
при 
-

-

-
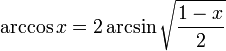
-

-


Получение функции arccos
Дана функция y = cos x. На всей своей области определения она является кусочно-монотонной, и, значит, обратное соответствие y = arccos x функцией не является. Поэтому мы рассмотрим отрезок, на котором она строго убывает и принимает все свои значения — [0;π]. На этом отрезке y = cos x строго монотонно убывает и принимает все свои значения только один раз, а значит, на отрезке [0;π] существует обратная функция y = arccos x, график которой симметричен графику y = cos x на отрезке [0;π] относительно прямой y = x.
Билет№16: y=arctg, y=arcctg определение, свойства.
Арктангенсом числа m называется такое значение угла α, для которого 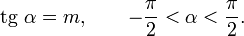
Функция 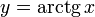 непрерывна и ограничена на всей своей числовой прямой. Функция
непрерывна и ограничена на всей своей числовой прямой. Функция 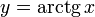 является строго возрастающей.
является строго возрастающей.
-
 при
при 
-
 при
при 
-
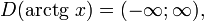
-
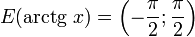
Свойства функции arctg
Получение функции arctg
Дана функция  На всей своей области определения она является кусочно-монотонной, и, значит, обратное соответствие
На всей своей области определения она является кусочно-монотонной, и, значит, обратное соответствие 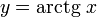 функцией не является. Поэтому рассмотрим отрезок, на котором она строго возрастает и принимает все свои значения только один раз —
функцией не является. Поэтому рассмотрим отрезок, на котором она строго возрастает и принимает все свои значения только один раз —  На этом отрезке
На этом отрезке  строго монотонно возрастает и принимает все свои значения только один раз, следовательно, на интервале
строго монотонно возрастает и принимает все свои значения только один раз, следовательно, на интервале  существует обратная
существует обратная 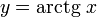 , график которой симметричен графику
, график которой симметричен графику  на отрезке
на отрезке  относительно прямой y = x.
относительно прямой y = x.

Арккотангенсом числа m называется такое значение угла x, для которого 
Функция  непрерывна и ограничена на всей своей числовой прямой. Функция
непрерывна и ограничена на всей своей числовой прямой. Функция  является строго убывающей.
является строго убывающей.
-
 при
при 
-
 при 0 < y < π,
при 0 < y < π, -

-

Свойства функции arcctg
-
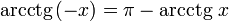 (график функции центрально-симметричен относительно точки
(график функции центрально-симметричен относительно точки 
-
 при любых x.
при любых x. -
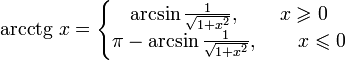
Получение функции arcctg
Дана функция  . На всей своей области определения она является кусочно-монотонной, и, значит, обратное соответствие
. На всей своей области определения она является кусочно-монотонной, и, значит, обратное соответствие  функцией не является. Поэтому рассмотрим отрезок, на котором она строго убывает и принимает все свои значения только один раз — (0;π). На этом отрезке
функцией не является. Поэтому рассмотрим отрезок, на котором она строго убывает и принимает все свои значения только один раз — (0;π). На этом отрезке  строго убывает и принимает все свои значения только один раз, следовательно, на интервале (0;π) существует обратная функция
строго убывает и принимает все свои значения только один раз, следовательно, на интервале (0;π) существует обратная функция  , график которой симметричен графику
, график которой симметричен графику  на отрезке (0;π) относительно прямой y = x. График симметричен к арктангенсу.
на отрезке (0;π) относительно прямой y = x. График симметричен к арктангенсу.

Билет№17: Основные тригонометрические тождества.
o sin² α + cos² α = 1
o tg α · ctg α = 1
o tg α = sin α ÷ cos α
o ctg α = cos α ÷ sin α
o 1 + tg² α = 1 ÷ cos² α
o 1 + ctg² α = 1 ÷ sin² α
Билет№18: Формулы кратных аргументов.
Формулы двойного угла
o cos 2α = cos² α - sin² α
o cos 2α = 2cos² α - 1
o cos 2α = 1 - 2sin² α
o sin 2α = 2sin α · cos α
o tg 2α = (2tg α) ÷ (1 - tg² α)
o ctg 2α = (ctg² α - 1) ÷ (2ctg α)
Билет№19: Формулы преобразования суммы и разности в произведение.





Билет№20: Формулы преобразования произведения.

| |

| |
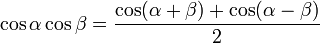
|
Билет№21:Формулы сложения.
o sin (α + β) = sin α · cos β + sin β · cos α
o sin (α - β) = sin α · cos β - sin β · cos α
o cos (α + β) = cos α · cos β - sin α · sin β
o cos (α - β) = cos α · cos β + sin α · sin β
o tg (α + β) = (tg α + tg β) ÷ (1 - tg α · tg β)
o tg (α - β) = (tg α - tg β) ÷ (1 + tg α · tg β)
o ctg (α + β) = (ctg α · ctg β + 1) ÷ (ctg β - ctg α)
o ctg (α - β) = (ctg α · ctg β - 1) ÷ (ctg β + ctg α)
Билет№22: Формулы понижения степени.
o sin² α = (1 - cos 2α) ÷ 2
o sin³ α = (3sin α - sin 3α) ÷ 4
o cos² α = (1 + cos 2α) ÷ 2
o cos³ α = (3cos α + cos 3α) ÷ 4
o sin² α · cos² α = (1 - cos 4α) ÷ 8
o sin³ α · cos³ α = (3sin 2α - sin 6α) ÷ 32
Билет№23: Формулы половинного аргумента.

Билет№24:Формулы приведения. Знаки функций по кругу.


 Формулы сложения функций выводятся из формул сложения аргументов (5), (6) и (7). Например, из формулы (5) следует:
Формулы сложения функций выводятся из формул сложения аргументов (5), (6) и (7). Например, из формулы (5) следует:
Билет№25:Универсальная подстановка.
Тождества имеют смысл, только когда существуют обе части (то есть при  ).
).
·  sin(α + β) + sin(α − β) = sin αcos β + cos αsin β + sin αcos β − cos αsin β =
sin(α + β) + sin(α − β) = sin αcos β + cos αsin β + sin αcos β − cos αsin β =
= 2sin αcos β.
То есть:
 — формула (29).
— формула (29).
Остальные формулы преобразования произведений функций выводятся аналогично.
· 












