Крестообразный маятник представляет собой металлическую ступицу А, вращающуюся с помощью подшипника относительно вала Б, который расположен горизонтально и одним концом жестко вмонтирован в стену (рис. 7.1). На ступице укреплены радиально четыре спицы С, вдоль которых могут перемещаться массивные тела В, закрепленные на спицах с помощью винтов. К шкиву ступицы крепится нить, которая наматывается на него. К свободному концу нити подвешивается груз массой m, под действием которого нить испытывает натяжение F, благодаря чему действие груза передается на шкив. При падении груза крестовина начинает вращаться. Определение момента инерции F крестообразного маятника производят, пользуясь основным уравнением динамики вращательного движения твердого тела относительно закрепленной оси
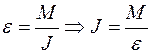. (7.1)
Рис. 7.1
Чтобы рассчитать момент инерции на основе уравнения (7.1), нужно знать момент силы относительно оси вращения М и угловое ускорение крестовины 
. Вращающий момент создается силой 
. Плечо этой силы относительно оси вращения равно радиусу шкива (рис. 7.1):
.
Силу F/ непосредственно мы найти не можем, но согласно третьему закону Ньютона она численно равна силе F, действующей со стороны нити на падающий груз. Груз движется поступательно под действием двух сил: силы тяжести 
и силы реакции нити F, равнодействующая этих сил сообщает грузу ускорение a. Запишем второй закон Ньютона для падающего тела:
,
откуда 
.
Неизвестным остается ускорение груза. Так как груз движется равноускоренно без начальной скорости, то высота падения груза
,
где t – время падения.
Величины h и t можно определить экспериментально и рассчитать ускорение 
.
Таким образом, вращающий момент равен
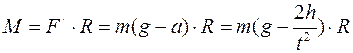. (7.2)
Теперь нужно найти угловое ускорение крестовины. Груз, падая с ускорением a, увлекает за собой нить, намотанную на шкив, поэтому точки обода шкива будут иметь такое же линейное ускорение, как и падающий груз.
Используя связь линейного ускорения с угловым, находим
. (7.3)
Выражаем момент инерции из уравнений (7.1), (7.2), (7.3):
.
Диаметр шкива можно измерить штангенциркулем и выразить радиус как 
.
Итак, расчетная формула для момента инерции крестообразного маятника следующая:
. (7.4)
Данный метод действие сил трения не учитывает.
Задание 1. Определение момента инерции крестообразного маятника при двух положениях грузов (на концах спиц, сдвинуты к ступице)
1. Измерить штангенциркулем диаметр шкива.
2. Намотать на шкив нить. Пользуясь прямоугольным треугольником и шкалой, укрепленной на стене, задать высоту падения груза.
3. Измерить время падения груза, для чего одновременно отпустить груз и включить секундомер. В момент удара о пол секундомер выключить.
4. Повторить опыт пять раз для случаев 1.2. и 1.3.
5. Результаты измерений занести в табл. 7.1. и рассчитать моменты инерции, сравнить их, сделать вывод.
Таблица 7.1
