Рентгеновские спектры атомов

Физика

Атомная и ядерная физика

 

Методические указания к расчётно-графическим работам и варианты заданий для студентов бакалавриата

направления 150400

 

 

САНКТ-ПЕТЕРБУРГ

УДК 531/534 (073)

 

Физика. АТОМНАЯ И ЯДЕРНАЯ ФИЗИКА: Методические указания к расчётно-графическим работам и варианты заданий для студентов бакалавриата направления 150400 / Национальный минерально-сырьевой университет «Горный». Сост. Т.В. Стоянова. СПб, 2014. 26 с.

 

Приведены рекомендации к выполнению расчётно-графических работ, теоретические основы дисциплины, пример решения задачи, библиографический список.

Расчётно-графические работы предназначены для студентов бакалавриата направления обучения 150400

 

Табл. 2. Ил. 4. Библ.: 5 назв.

 

Научный редактор доц. Н.А. Тупицкая

 

 

Ó Национальный минерально-сырьевой университет «Горный»,2014 г.

 

 

РЕКОМЕНДАЦИИ К ВЫПОЛНЕНИЮ РАСЧЁТНО-ГРАФИЧЕСКОЙ РАБОТЫ

 

Вопросы и задачи, содержащиеся в пособие, охватывают большую часть стандартного курса квантовой механики, изучаемого в технических вузах, и способствуют более глубокому усвоению теоретического материала данного раздела.

Выполнение расчётно-графической работы предполагает достаточно большой объём самостоятельной работы студента.

Перед выполнением расчётно-графической работы рекомендуется изучить лекционный курс на тему «Атомная и ядерная физика», познакомиться с соответствующим разделом учебника общего курса физики. Если при самостоятельном изучении теоретического материала возникли вопросы, желательно обсудить их на практических занятиях, но если и после этого остались не ясные моменты, можно получить индивидуальную консультацию преподавателя, ведущего расчётно-графическую работу или лектора.

При изучении физического явления, прежде всего, необходимо выяснить сущность явления, условия при которых оно возможно, определить с помощью каких физических величин, оно характеризуется. Желательно понять, как оно связано с другими явлениями и возможности его применения на практике: При определении физической величины важно обратить внимание на то, какая это величина – скалярная или векторная, какие свойства она характеризует, выяснить её размерность и формулу, определяющую связь с другими физическими величинами. При прочтении закона обратите внимание на границы его применения, определите, между какими явлениями он выражает связь, уточните формулировку и математическое выражение закона.

Расчётно-графическая работа оформляется на компьютере. При выполнении расчётно-графической работы необходимо указать на титульном листе: название института, наименование дисциплины, название работы, фамилию и инициалы студента и ведущего расчётно-графическое задание преподавателя, год выполнения работы.

Необходимо полностью переписать задачу своего варианта, а заданные физические величины выписать отдельно, при этом все числовые значения должны быть переведены в одну систему единиц. При получении расчётной формулы приведите её полный подробный вывод.

Математическое решение должно сопровождаться пояснениями, а в случае необходимости его можно продемонстрировать рисунком. Задачу рекомендуется решить сначала в общем виде (в буквенных обозначениях), поясняя применяемые при написании формул буквенные обозначения, и только после проверки размерности искомой физической величины подставить в выведенную формулу числовые значения. Все необходимые числовые значения величин должны быть выражены в системе «СИ». После получения окончательного результата, для удобства построения графических зависимостей, можно перейти к вне системным единицам. Например, выразить энергию в электрон-вольтах.

Перед построением графиков необходимо получить аналитическое выражение функциональной зависимости. Выбрать удобный масштаб и указать его на осях координат, а так же физические величины и единицы измерения.

На координатной плоскости обязательно должны быть нанесены экспериментальные точки. Кривая, аппроксимирующая функциональную теоретическую зависимость строится в соответствии с методом наименьших квадратов.

 

СОДЕРЖАНИЕ ОТЧЁТА

1. Титульный лист

2. Теоретическая часть:

2.1. Определения всех физических явлений, законов и величин, встречающихся в данной работе.

2.2. Основные расчётные формулы с пояснениями.

3. Расчётная часть:

3.1. Задание с исходными данными своего варианта.

3.2. Расчёт с пояснениями.

3.3. Графики.

4. Анализ результатов. Заключение.

 

ТЕОРЕТИЧЕСКИЕ ОСНОВЫ АТОМНОЙ И ЯДЕРНОЙ ФИЗИКИ

Наиболее вероятное расстояние электрона в состоянии n от ядра:

, (1)

где m_e – масса электрона, Z – заряд ядра (атомный номер), n = 1, 2, 3… – главные квантовые числа. При n = 1 и Z = 1 это расстояние совпадает с радиусом первой боровской орбиты.

Одновременное измерение модуля момента импульса и трёх его проекций на оси координат в квантовой механике невозможно. Модуль момента импульса определяется:

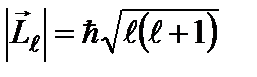. (2)

Число ℓ = 0, 1, 2, …, n -1 называется орбитальным квантовым числом. Проекция момента импульса на любую ось (z) тоже может принимать лишь определенные значения

, (3)

где m_ℓ = 0, ± 1, ± 2, …, ± ℓ и называется магнитным квантовым числом. Такое название связано с тем, что оно определяет также проекцию магнитного момента, создаваемого движением электрона вокруг ядра:

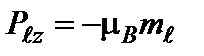. (4)

Модуль магнитного момента электрона

, (5)

где = 0,927∙10^-23 Дж/Тл – магнетон Бора. Гиромагнитное отношение для орбитальных магнитного и механического моментов

. (6)

Электрон обладает также собственным механическим моментом импульса, равным

, (7)

где s = 1/2 – спиновое квантовое число. Соответствующий ему магнитный момент также квантован

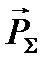
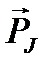
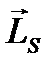
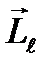
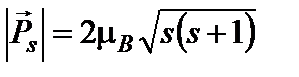. (8)

Проекции спинового момента импульса и магнитного момента на направление внешнего магнитного поля равны

Рис.1. Сложение моментов. оментовпереходов

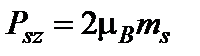и , (9)

где m_s – спиновое квантовое число, может принимать значения ± 1/2.

Гиромагнитное отношение для спиновых магнитного и механического моментов оказывается в два раза больше, чем для орбитальных моментов

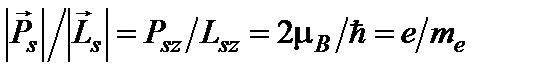. (10)

Орбитальный и спиновый моменты импульса электрона складываются и дают полный момент импульса электрона 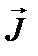(рис.1). Модуль полного момента импульса квантуется:

, (11)

где 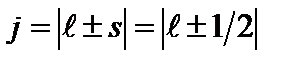- внутреннее квантовое число. Проекция полного момента импульса на направление внешнего магнитного поля

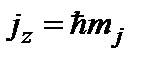, (12)

где m_j может принимать 2 j +1 значение от – j до j.

Таким образом, для описания состояния электрона в атоме используют четыре квантовых числа: n, ℓ, m_ℓ и m_s. или n, ℓ, j, m_j. Из-за разных гиромагнитных отношений для спинового и орбитального моментов суммарный магнитный момент оказывается не параллельным суммарному механическому моменту. Поэтому вводится специальный коэффициент g -фактор Ланде, который есть не что иное, как коэффициент пропорциональности между 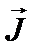и :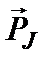

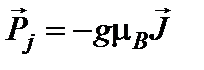, (13)

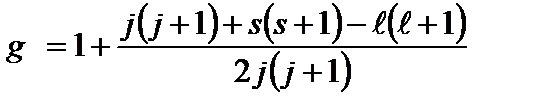. (14)

Порядок заполнения уровней в атоме определяется эмпирическими правилами Клечковского.

Первое правило Клечковского: сначала будут заполняться уровни с наименьшей суммой квантовых чисел n + ℓ.

Второе правило Клечковского: если два уровня имеют одинаковую сумму квантовых чисел n + ℓ, то первым будет заполняться энергетический уровень с меньшим значением n.

Электроны подчиняются принципу Паули: каждый энергетический уровень может быть заселен не более чем двумя электронами с противоположными спинами.

Вырожденные состояния электроны заселяют таким образом, чтобы спин 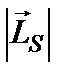атома был максимален и, при этом по возможности максимальным было значение 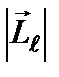– правило Гунда.

 

Рентгеновские спектры атомов

 

Экспериментально строение атомов изучают, исследуя спектры испускания и поглощения атомами электромагнитного излучения. Оптический диапазон соответствует переходам валентных электронов.

Для атома водорода формула, описывающая спектральные линии, подобрана экспериментально и называется формулой Бальмера – в честь ученого, впервые получившего ее для спектрального диапазона видимого излучения. Схема переходов приведена на рис.2.

Длины волн излучаемых атомом водорода определяются по формуле:

, (15)

Kα

Kβ

Kγ

К -серия

L -серия

Возбуждение К -серии

Возбуждение L -серии

К

L

M

N

n

Рис.2. Схема переходов.

где м^-1 – постоянная Ридберга; и 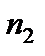– главные квантовые числа, соответствующие энергетическим уровням, между которыми совершается электронный переход в атоме. Длина волн излучаемых водородоподобными ионами с зарядовым числом ядра Z (число Z определяется по номеру химического элемента в таблице Менделеева), могут быть рассчитаны по формуле:

. (16)

Водородоподобными ионами называют атомы с одним электроном на внешней оболочке.

Рентгеновское излучение возникает при переходах на внутренних оболочках. Частоты и длины волн соответствующего излучения можно определить, используя закон Мозли:

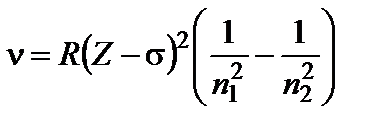, (17)

, (18)

где Z – порядковый номер элемента в системе Менделеева, R и R' – постоянные Ридберга для частот и длин волн (R = 3,29 ∙ 10¹⁵ c^-1 и R' = 1,10 ∙ 10⁷ м^-1), n₁ – номер уровня, с которого переходит электрон, n₂ – номер уровня, на который переходит электрон. Величина σучитывает экранировку внутренними электронами Кулоновского взаимодействия ядра и рассматриваемого электрона и называется постоянной экранирования.

Правила отбора для электромагнитных переходов:

Δ j = 0, ±1; Δ m_j = 0, ±1; Δ ℓ = ±1; Δ m_ℓ = 0, ±1; Δ m_s = 0