Цель работы:
1) определение изменения температуры углекислого газа при протекании через малопроницаемую перегородку при разных начальных значениях давления и температуры;
2) вычисление по результатам опытов коэффициентов Ван-дер-Ваальса "a" и "b".
Молекулярно-кинетическая теория газов основывается на модели идеального газа. В этой модели пренебрегается размерами молекул по сравнению с расстоянием между ними, т.е. молекулы рассматриваются как материальные точки. Кроме того, пренебрегается силами взаимодействия между молекулами (за исключением моментов столкновения). Обычные газы при невысоких давлениях можно рассматривать как идеальные.
Уравнение состояния для идеального газа это уравнение Менделеева - Клапейрона. Для одного моля газа оно имеет вид:
При больших давлениях расстояния между молекулами мало, и размерами молекул уже нельзя пренебрегать по сравнению с этим расстоянием. Кроме того, при малых расстояниях между молекулами следует учитывать взаимодействие между ними (силы притяжения и отталкивания). Поэтому при высоких давлениях свойства реальных газов отличаются от свойств идеальных газов.
Состояние реальных газов описывается уравнением Ван-дер-Ваальса, которое имеет вид (для одного моля)
Здесь a и b – константы Ван-дер-Ваальса. Поправка 
дает внутреннее давление pi, обусловленное взаимным притяжением молекул друг к другу. Константа b – определяет ту часть объема, которая недоступна для движения молекул вследствие их конечных размеров.
Внутренняя энергия идеального газа состоит из кинетической энергии, движения молекул и потенциальной энергии взаимодействия молекул
Кинетическая энергия зависит только от температуры газа Т
где СV – молярная теплоемкость при постоянном объеме.
Потенциальная энергия взаимодействия молекул зависит от их расстояния друг от друга и, следовательно, от объема занимаемого газом. При расширении газа должна быть совершена работа по преодолению сил притяжения между молекулами, т.е. против внутреннего давления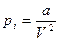 
.
Эта работа идет на увеличение потенциальной энергии
Интегрирование этого выражения дает для потенциальной энергии
Таким образом, внутренняя энергия реального газа является функцией двух параметров: Т и V
Для идеального газа взаимодействием между молекулами пренебрегается, поэтому внутренняя энергия идеального газа состоит только из кинетической энергии молекул и зависит только от температуры.
Согласно первому закону термодинамики количество тепла, подводимого к системе, идет на приращение внутренней энергии системы и на совершение этой системой работы A над внешними телами 
Если газ расширяться адиабатическим, т.е. без теплообмена с окружающей средой, то Q=0
Если при адиабатическом расширении газ не будет совершать внешней работы (А=0) (при расширении в пустоту), то 
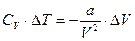
Отсюда следует, что D T и D V имеют разные знаки. При расширении D V >0, D T <0. Следовательно, при адиабатическом расширении в пустоту реальный газ должен охлаждаться.
В случаях идеального газа в этих условиях
D T =0 Т=const
Т.е при адиабатическом расширении идеального газа в пустоту его температура не должна меняться.
В середине XIX века английские ученые Джоуль и Томсон экспериментально обнаружили, что при адиабатическом расширении газа без совершения им полезной работы температура газа изменяется. Это явление получило название эффекта Джоуля-Томсона.
Схема опыта Джоуля-Томсона приведена на рис. 1. В хорошо теплоизолированную трубу вставлена пористая перегородка (пробка). Слева и справа от пробки поддерживаются постоянные давления p 1и p 2 (p 1> p 2). Под действием перепада давлений D p=p 1 -p 2 газ продавливается через пробку и при этом адиабатически расширяется от давления р 1 до давления р 2. Измерялась разность температур D T =T2-T1
Представим себе, что определенная порция газа, например, 1 моль, протекает слева направо через пористую перегородку П. Вначале этот газ занимает объем V 1 между перегородкой и сечением 1, а после прохождения перегородки, т.е. после расширения, - объем V 2 между перегородкой и сечением 2’. Для наглядности поместим мысленно в сечение 1 поршень перемещение которого вправо и вызывает протекание газа через перегородку под постоянным давлением p 1. После прохождения через перегородку этот же газ перемещает воображаемый поршень K 2 из положения 2 в положение 2’. В действительности роль поршней K 1 и K 2 выполняет компрессор.
На основании первого закона термодинамики можно написать
Так как труба теплоизолированная, то процесс расширения будет адиабатическим
(1)
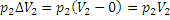
-работа, произведенная над газом при вытеснении его из объема 
-работа, произведенная газом при перемещении поршня справа от перегородки
Тогда уравнение (1) запишется так
(2)
Преобразуем равенство (2), сделав некоторые упрощения. В левой части давление 
большое, поэтому газ здесь будем считать реальным, а в правой части давление 
невелико и, следовательно, газ можно считать идеальным.
Тогда 
(3)
(4) - Из уравнения Ван-дер-Ваальса
(5) 
(6)
Подставим (3),(4),(5) и (6) в формулу (2) 
(7)
Третье слагаемое можно записать в виде
(8)
С учетом этого уравнение(7) перепишется так
Отсюда получим формулу для изменения температуры газа при протекании через пористую перегородку
(9)
Как видно, знак 
определяется знаком выражения, стоящего в скобках.
Если можно пренебречь поправкой а (а=0), то >0, 
т.е при расширении газ нагревается. Это отрицательный эффект Джоуля -Томсона
Если можно пренебречь поправкой b (b=0), то <0, 
газ охлаждается. Это положительный эффект Джоуля- Томсона.
Для одного и того же газа в зависимости от его температуры и давления, может играть большую роль то поправка а, то поправка b. Поэтому один и тот же газ в зависимости от внешних условий может давать или положительный, или отрицательный эффект Джоуля-Томсона.
При некоторых условиях (скобка в уравнении (9) равна 0) может быть нулевой эффект. Эта температура называется температурой инверсии.
Из формулы (9) видно также, что для идеального газа (поправки а и b равны 0) 
то есть температура идеального газа при таком расширении не меняется, т.е эффект Джоуля-Томсона отсутствует.
Для количественной оценки эффекта вводится коэффициент Джоуля-Томсона. При некоторых упрощающих предположениях он имеет вид
(10)
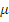<0-отрицательный эффект Джоуля-Томсона
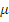>0- положительный эффект Джоуля-Томсона
Температура инверсии 
получается из равенства нулю скобки в уравнении (10)
(11)
Критическая температура для реальных газов также выражается через поправки а и b
(12)
Сравнивая (11) и (12) получаем следующее простое соотношение между температурой инверсии и критической температурой
(13)
