Схема привода
 2
2
 1 P
1 P 




 2 n2
2 n2
III



 | |||
 | |||
 |
 aω
aω





 II
II
P3 n3
1-шестерня; 2-колесо
Задачи расчета
· Выбор материалов и вида термообработки зубчатых колес передачи;
· Определение геометрических параметров передачи;
· Определение сил в зацеплении;
· Выполнение проверочного расчета на контактную прочность и изгиб;
Данные для расчета
Исходными данными для расчета являются силовые и кинематические параметры передачи, приведенные в таблице 2.1
Таблица 2.1 —Таблица силовых и кинематических параметров редуктора
| вал | мощность Р, кВт | частота вращения n, мин-1 | угловая скорость ω, с-1 | вращающий момент Т нМ |
| 9.02 | 560.8 | 58.7 | ||
| 8.7 | 14.7 |
Условия расчета
Надежная работа закрытой зубчатой передачи обеспечена при соблюдении условий прочности по контактным напряжениям и напряжениям изгиба.
σ н.расч < [σ]н , σF расч < [σ]F,
где σ н.расч и σF расч –соответственно расчетные контактные и изгибные напряжения проектируемой передачи;
[σ]н и [σ]F –соответственно допускаемые контактные и изгибные напряжения материалов колес.
Допускается недогрузка передачи— σ н < [σ]н не более 10% и перегрузка σ н.< [σ]н до 5%.
0.9[σ]F < σF1 < 1.05[σ]F
Расчет передачи
2.5.1 Выбор материалов для изготовления зубчатых колес.
Так как мощность привода < 10кВт, для изготовления зубчатых колес принимаем: Для колеса Сm40x термообработка улучшение с Нвср=248, для шестерни: Сm40x термообработка улучшение до твердости Нвср=285. Нв1=Нв2+(20-50)=285-248=37 Условие выполняется.
2.5.2 Определяем допускаемые напряжения
По таблице определяем, величину допускаемых контактных напряжений, в зависимости от твердости.
[σ]Но=1.8Нвср+67мПа
Принимаем коэффициент долговечности КHL=КFL=1,0 Тогда
[σ]н1= КHL[σ]н+67=1,0 1,8 285+67=580мПА
[σ]н2= КHL[σ]н2+67=1,0 1,8 249+67=514мПА
В качестве расчетной принимаем:
[σ]н=0.45([σ]н1+[σ]н2)=0.45(580+514)=493мПА
Допускаемое напряжение изгиба: [σ]Fo=1.03Нвср
[σ]F1= KFL[σ]Fо1=1 1.03 285=294мПА
[σ]F2= KFL[σ]Fо2=1 1.03 248=256мПА
2.5.3 Определяем межосевое расстояние
аω=КL(u+1)  ,
,
аω=430(4+1) 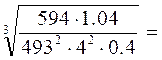 160
160
2.5.4 Определяем геометрические параметры передачи
Нормальный модуль
mn=(0.01—0.02) аω=1,6—3,2
Берем среднее значение mn=2,0
Определяем число зубьев шестерни
Z1= 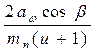
β-угол наклона зубьев, берем 10о; cos10o=0,98, тогда
Z1=  Принимаем Z1=31
Принимаем Z1=31
Тогда Z2= Z1 U=31* 4=124
Уточняем U: 
Уточняем β: 
Определим диаметры:
· Делительный
d1= mnZ1/cosβ=2,0 *31/0.9687=64мм
d2=mnZ2 /cosβ=2,0 * 124/0,9687=256мм
· Диаметры окружности вершин
da1=d1+2mn=64+2 * 2=68мм
da2=d2+2mn=256+2 * 2=260мм
· Диаметры окружности впадин
df1=d1-2,5mn=64-2,5 * 2=59мм
df2=d2-2,5mn=256-2,5 * 2=251мм
Ширина венца колеса:
b2= аω ψba=160 * 0.4=64мм
b2=65мм
b1=b2+(5-10)мм=75мм
Данные своди в таблицу геометрических параметров передачи.
Таблица 2.1 -Геомертические параметры зубчатого зацепления
| параметры | шестерня | колесо |
| Межосевое расстояние | ||
| Модуль зацепления | ||
| Угол наклона зубьев,β | ||
| Число зубьев, Z | ||
| Делительный диаметр,d мм | ||
| Диаметр вершин зубьев, da мм | ||
| Диаметр впадин зубьев, df мм | ||
| Ширина венца b, мм |

|
аω=  мм
мм
Определим окружную скорость колес


Для данной скорости по таблице назначаем восьмую степень точности изготовления зубчатых колес.
2.5.5 Определение силовых параметров зацепления

|
Окружное усилие:
 Н
Н
Радиальное усилие:
Fr=Ft tgα/cosβ
α-200; tg200=0,364
Fr=4800 0,364/0,9696=1801H
Осевое усилие:
Fα= Fr tgβ=4800 /0,2568=1233H
2.5.6 Проверочный расчет передачи:
а) По контактному напряжению:

k-376-для косозубой передачи
Кнα=1.22 -коэффициент учитывающий неравномерность распределения нагрузки между зубьями.
Кнβ=1.04 - коэффициент учитывающий неравномерность распределения нагрузки по длине контактной линии зуба
Кнv=1.02 - коэффициент учитывающий влияние динамической нагрузки
 МПа
МПа
σн=478<[σ]=493

б) По напряжению изгиба
σf2=Уf2Уβ 
Zv1=z1/cos3β=31/0.96963=35.2 принимаем Zv1 =35
Zv2=z2/cos3β=124/0.96963=140.9 принимаем Zv2 =141
Уβ=1- β/1400=0.89
σf2=139мПа<[σ]
σf1= σf2 Уf1/ Уf2=144мПА
Условия выполняются.
Заключение: результаты проверочных расчетов по контактным напряжениям и напряжениям изгиба показывают, что полученные геометрические параметры редуктора удовлетворяют заданным.






