КУРСОВОЙ ПРОЕКТ
по разделу 1 Объектно-ориентированное программирование
междисциплинарного курса 01.02. Прикладное программирование
Решение системы линейных алгебраических уравнений
Методом Гаусса средствами языка программирования Visual Basic
Выполнил студент
3 курса, группы ПО-31
Хуснияров И. З.
Руководитель
Аришина В. Ф.
Оценка ______________
2013
Содержание
| Введение | |
| Теоретическая часть | |
| Системы линейных алгебраических уравнений | |
| Решение систем линейных уравнений графическим способом | |
| Метод Гаусса | |
| Visual Basic | |
| Практическая часть | |
| Описание программы | |
| Работа программы | |
| Заключение | |
| Список использованной литературы | |
| Приложение А (программный код) |
Ведение
В курсовом проекте рассмотрена программа, реализующая приближенное решение систем линейных уравнений графическим способом, с подключением модуля “Метод Гаусса”, созданная в среде программирования Visual Basic 2010.
Системы линейных уравнений, описывают экономические процессы в обществе и производстве. Навыки решения таких систем я вляются профессионально необходимыми и демонстрируют готовность студента к профессионльной деятельности. Автоматизировать процесс решения таких систем поможет программный продукт, представленный в данном курсовом проекте. Программа написана средствами языка программирования Visual Basic, обладающего возможностями, которые помогут решить графически систему линейных уравнений, а так же реализовать метод Гаусса. Метод Гаусса выбран ак универсальный для систем линейных уравнений.
Цель курсового проекта:
Разработать код программного продукта, реализующего приближенное решение систем линейных уравнений графическим способом, с подключением модуля, реализующего метод Гаусса решения систем линейных уравнений.
Задачи курсового проекта:
1. Разработать программный код модуля, реализующего приближенное решение систем линейных уравнений графическим способом.
2. Выполнить отладку программного модуля «Метод Гаусса» и приближенного решения с использованием специализированных программных средств.
3. Выполнить тестирование программного модуля «Метод Гаусса» и приближенного решения по составленным тестовым заданиям.
4. Подготовить документацию с использованием информационно-коммуникационных технологий.
Теоретическая часть
Системы линейных алгебраических уравнений.
Система m линейных алгебраических уравнений с n неизвестными (или, линейная система, также употребляется аббревиатура СЛА́У) в линейной алгебре — это система уравнений вида

Где m -количество линейных уравнений;
n -количество переменных;
x1, x2, …, xn — неизвестные, которые надо определить;
a11, a12, …, amn — коэффициенты системы;
b1, b2, … bm — свободные члены;
Система называется однородной, если все её свободные члены равны нулю (b1 = b2 = … = bm = 0), иначе — неоднородной.
Система называется квадратной, если число m уравнений равно числу n неизвестных.
Решение системы — совокупность n чисел c1, c2, …, cn, таких что подстановка каждого ci вместо xi в систему обращает все её уравнения в тождества.
Система называется совместной, если она имеет хотя бы одно решение, и несовместной, если у неё нет ни одного решения.
Совместная система вида может иметь одно или более решений.
Совместная система вида называется определённой, если она имеет единственное решение; если же у неё есть хотя бы два различных решения, то она называется неопределённой. Если уравнений больше, чем неизвестных, она называется переопределённой.
Матричная форма.
Система линейных уравнений может быть представлена в матричной форме как:

Или:
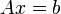
Где A — это матрица системы,
x — столбец неизвестных,
b — столбец свободных членов.
Если к матрице A приписать справа столбец свободных членов, то получившаяся матрица называется расширенной.
Эквивалентные системы линейных уравнений
Системы линейных уравнений называются эквивалентными, если множество их решений совпадает, то есть любое решение одной системы одновременно является решением другой, и наоборот.
Систему, эквивалентную данной, можно получить, в частности, заменив одно из уравнений на это уравнение, умноженное на любое отличное от нуля число. Эквивалентную систему можно получить также, заменив одно из уравнений суммой этого уравнения с другим уравнением системы. В общем, замена уравнения системы на линейную комбинацию уравнений даёт систему, эквивалентную исходной.
Система линейных алгебраических уравнений
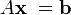
эквивалентна системе
 ,
,
Где C — невырожденная матрица.
В частности, если сама матрица A — невырожденная, и для неё существует обратная матрица A-1, то решение системы уравнений можно формально записать в виде
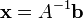 .
.
Решение систем линейных уравнений графическим способом
Решение систем линейных уравнений графическим способом заключается в построении графика каждого уравнения, входящего в данную систему, в одной координатной плоскости и нахождении точки пересечения этих графиков. Координаты этой точки (x; y) и будут являться решением данной системы уравнений.
Если прямые, являющиеся графиками уравнений системы, пересекаются, то система уравнений имеет единственное р ешение.
Если прямые, являющиеся графиками уравнений системы, параллельны, то система уравнений не имеет решений.
Если прямые, являющиеся графиками уравнений системы, совпадают, то система уравнений имеет бесконечное множество решений.
Примеры
Графиком каждого уравнения служит прямая линия, для построения которой достаточно знать координаты двух точек. Мы составили таблицы значений х и у для каждого из уравнений системы.

Прямую y=2x-3 провели через точки (0; -3) и (2; 1).
Прямую y=x+1 провели через точки (0; 1) и (2; 3).
Графики данных уравнений системы 1) пересекаются в точке А(4; 5). Это и есть единственное решение данной системы.
Ответ: (4; 5).

Выражаем у через х из каждого уравнения системы, а затем составим таблицу значений переменных х и у для каждого из полученных уравнений.
Прямую y=2x+9 проводим через точки (0; 9) и (-3; 3).
Прямую y=-1,5x+2 проводим через точки (0; 2) и (2; -1).
Наши прямые пересеклись в точке В (-2; 5).
Ответ: (-2; 5).
Метод Гаусса
Метод Гаусса — классический метод решения системы линейных алгебраических уравнений (СЛАУ). Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе треугольного вида, из которой последовательно, начиная с последних (по номеру), находятся все переменные системы.
Пусть исходная система выглядит следующим образом


Где A называется основной матрицей системы,
b — столбцом свободных членов.
Тогда, согласно свойству элементарных преобразований над строками, основную матрицу этой системы можно привести к ступенчатому виду (эти же преобразования нужно применять к столбцу свободных членов):


При этом будем считать, что базисный минор (ненулевой минор максимального порядка) основной матрицы находится в верхнем левом углу, то есть в него входят только коэффициенты при переменных xj1 ,…, x jr.
Тогда переменные xj1 ,…, x jr называются главными переменными. Все остальные называются свободными.
Если хотя бы одно число Bi ≠0, где i>r,то рассматриваемая система несовместна, т.е. у неё нет ни одного решения.
Пусть Bi =0 для любых i>r.
Перенесём свободные переменные за знаки равенств и поделим каждое из уравнений системы на свой коэффициент при самом левом x:

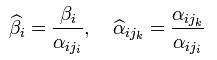
Если свободным переменным системы придавать все возможные значения и решать новую систему относительно главных неизвестных снизу вверх (то есть от нижнего уравнения к верхнему, то мы получим все решения этой СЛАУ. Так как эта система получена путём элементарных преобразований над исходной системой, то по теореме об эквивалентности при элементарных преобразованиях системы эквивалентны, то есть множества их решений совпадают.
Разрешается:
изменять порядок строк матрицы, что соответствует изменению порядка уравнений;






