К основным алгоритмическим конструкциям относятся: линейная, разветвленная (ветвящаяся) и циклическая.
 |  | ||
Да Нет
| ||||
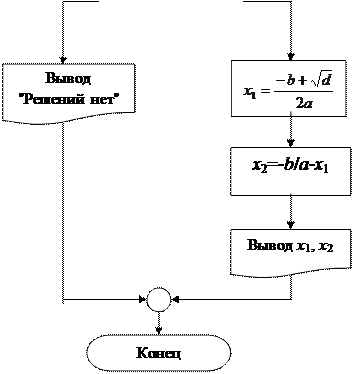
| Рис. 13.2 – Линейная структура | Рис. 13.3 – Разветвленная структура |
Линейным принято называть вычислительный процесс, в котором операции выполняются последовательно, в порядке их записи. Каждая операция является самостоятельной, независимой от каких-либо условий. При записи алгоритма в виде блок-схемы блоки, отображающие эти операции, располагаются в линейной последовательности.
Линейные вычислительные процессы имеют место, например, при вычислении арифметических выражений, когда имеются конкретные числовые данные и над ними выполняются соответствующие условию задачи действия. На рис. 13.2 показан пример линейного алгоритма вычисления арифметического выражения
y =(b 2-4 ac)/(a + c).
Вычислительный процесс называется ветвящимся, если для его реализации предусмотрено несколько направлений (ветвей). Каждое отдельное направление процесса обработки данных является отдельной ветвью вычислений. Ветвление в программе – это выбор одной из нескольких последовательностей команд при выполнении программы. Выбор направления зависит от заранее определенного признака, который может относиться к исходным данным, к промежуточным или конечным результатам. Признак характеризует свойство данных и имеет два или более значений.
Ветвящийся процесс, включающий в себя две ветви, называется простым, более двух ветвей – сложным. Сложный ветвящийся процесс можно представить с помощью простых ветвящихся процессов.
Направление ветвления выбирается логической проверкой, в результате которой возможны два ответа: "да" – условие выполнено, и "нет" – условие не выполнено.
Следует иметь в виду, что хотя на схеме алгоритма должны быть показаны все возможные направления вычислений в зависимости от выполнения определенного условия (или нескольких условий), при однократном прохождении программы процесс реализуется только по одной ветви, а остальные исключаются. Любая ветвь, по которой осуществляются вычисления, должна приводить к завершению вычислительного процесса.
На рис. 13.3 в качестве алгоритма разветвленной структуры показан пример алгоритма вычисления корней квадратного уравнения.
Циклическими называются программы, содержащие циклы. Циклом называется многократно повторяющееся действие или группа действий (участок программы).
В организации цикла можно выделить следующие этапы:
· подготовка (инициализация) цикла;
· многократно повторяющееся действие или группа действий (тело цикла);
· изменение параметров;
· проверка условия завершения цикла.
Порядок выполнения этих этапов может изменяться. В зависимости от расположения проверки условия завершения цикла различают циклы, организованные по схеме "До" и циклы, организованные по схеме "Пока" (рис. 13.4). Для цикла, организованного по схеме "До" (рис. 13.4 а), тело цикла выполняется как минимум один раз, так как сначала выполняются вычисления, а затем производится проверка условия завершения цикла. В случае цикла "Пока" (рис. 13.4 б) тело цикла может не выполниться ни разу при условии, что первая проверка подтвердила завершение цикла.
|

| |||||||||||||
| а | б | |||||||||||||
| Рис. 13.4 – Циклическая структура |
Цикл называется детерминированным, если число повторений тела цикла заранее известно или определено. Цикл называется итерационным, если число повторений тела цикла заранее неизвестно, а зависит от значений параметров (некоторых переменных), участвующих в вычислениях.
Базовые алгоритмы
К базовым алгоритмам принято относить алгоритм вычисления суммы (произведения) последовательности чисел, поиск наибольшего (наименьшего) элемента в заданной последовательности чисел, вычисление значений функции на заданном промежутке с заданным шагом изменения аргумента.
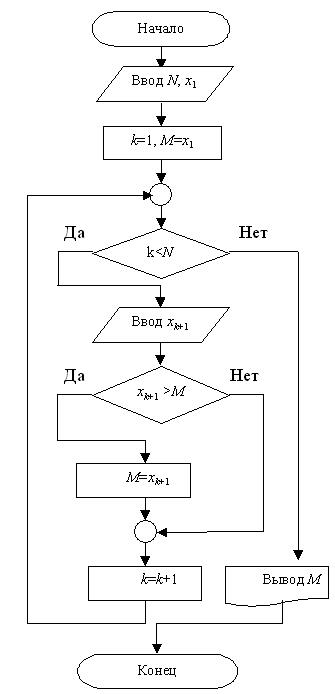
На рис. 13.5 и 13.6 представлены алгоритмы вычисления суммы и нахождения наибольшего элемента.
| 
| ||||||
| Рис. 13.5 - Вычисление суммы | Рис. 13.6 - Нахождение наибольшего элемента |
Алгоритм вычисления суммы показан в виде цикла "До" с условием завершения, а алгоритм поиска наибольшего числа – в виде цикла "Пока" с условием продолжения.












 Да Нет
Да Нет