Задание:
· Вывод математического дифференциального уравнения объекта регулирования по его передаточной функции.
· Нахождение решения полученного дифференциального уравнения при единичном входном воздействии и нулевых начальных условиях.
· Расчет и построение графика переходной функции объекта регулирования.
Различают статические и динамические характеристики элементов системы. Статической характеристикой называют зависимость выходного сигнала элемента от входного в установившемся состоянии. Динамическая характеристика – это реакция системы на возмущение (зависимость изменения выходных переменных, входных и от времени).
Переходной характеристикой называют реакцию системы на ступенчатое единичное входное воздействие при нулевых начальных условиях (из установившегося состояния). В качестве математической модели объекта управления используются обыкновенные дифференциальные уравнения или их различные преобразования.
Дифференциальное уравнение звеньев и систем в общем виде можно представить, как
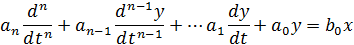
Где ai (i=1,2…n), b0 – постоянные коэффициенты; x,y – величины входного и выходного сигналов.
Другим математическим описанием динамики звеньев и систем является аппарат передаточных функций. Методика получения передаточной функции объекта регулирования по дифференциальному уравнению приведена в приложении Б. Согласно ей возможно решение обратной задачи: получение дифференциального уравнения из передаточной функции.
Для расчета и построения временной характеристики объекта регулирования следует найти решение его дифференциального уравнения.
В полученном выражении решения дифференциального уравнения задается значение времени t и строим графи временной характеристики объекта.
Составим математическое дифференциальное уравнение объекта регулирования по его передаточной функции.
Дано дифференциальное уравнение
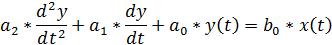
Определим математическое выражение передаточной функции
Решение.
1. Применим к дифференциальному уравнению преобразование Лапласа. При нулевых начальных условиях справедливы формулы преобразования операций дифференцирования:
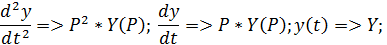
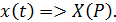
2. Дифференциальное уравнение, преобразованное по Лапласу, записывается в виде
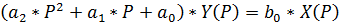
3. Отношение изображений выходного сигнала Y(P) ко входному X(P) при нулевых начальных условиях называется передаточной функцией W(P):
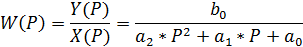
Возможен обратный расчет. По известной передаточной функции можно найти дифференциальное уравнение.






