Определение предела последовательности
Последовательность называется отображение
f:N->A (в любое множество), A⊂R то последовательность называется числовой.
an – элемент числовой последовательности
{an}  - элемент числовой последовательности
- элемент числовой последовательности
Числовая последовательность может быть задана перечислением.
A – конечно:
a1=1, a2=1, …, an=1
любо формулой его общего члена
an=  , a1=1, a2=
, a1=1, a2=  , …, an=
, …, an=  .
.
Определение предела числовой последовательности.
Число a называется пределом числовой последовательности {an}, если  n
n  <
< 
a=(равно по определению) =  n
n
Пример
an=  ;
;  n=0 (a=0)
n=0 (a=0)
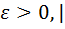 a n
a n  =|
=|  , n>
, n> 
N=[  ]+1
]+1
Если последовательность имеет предел, то называется сходящаяся, в противном случае расходящаяся.
При отрицании какого-нибудь высказывания кванта всеобщности  меняется.
меняется.
Запишем, что число a не является пределом последовательности
(a<>liman)( =>|an-a|
=>|an-a| 
an=(-1)n:-1;1;-1;1; …

 –окрестностей числа a называется такой интервал (a-
–окрестностей числа a называется такой интервал (a- 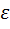 ,a+
,a+ 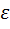 )
)
Ʊ(a, 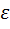 ) окрестностей.
) окрестностей.
Число a является пределом числовой последовательности любая ее Ʊ(a, 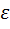 ) содержит все члены этой последовательности за исключением, быть может, конечного числа.
) содержит все члены этой последовательности за исключением, быть может, конечного числа.
Общее свойство пределов
1)Теорема!!! Сходящаяся последовательность имеет только один предел
Док-во:
Предположим противное(ПП)
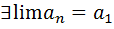 ,
,  ;
;  ,
,

 ,
,
Ʊ( ⋂ Ʊ(
⋂ Ʊ( <> ∅
<> ∅




 , ч.т.д
, ч.т.д
2) Элементы сходящихся последовательности являются ограниченным множеством.
Док-во:

Например

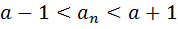
A{ a N+1, aN+2, … } ⊂ (a -1, a+1)
B={ a 1, a 2, …, a N}
A∪B –огран. чтд
3) 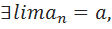 b>a =>
b>a =>  =>
=> 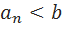
чтд 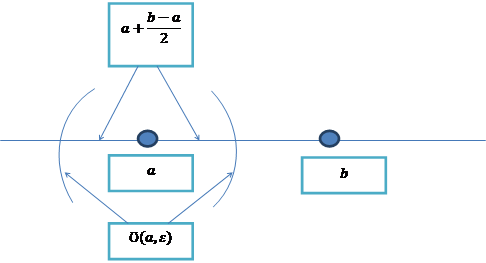 c<a =>
c<a =>  =>
=> 
4) 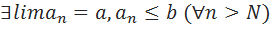 =>
=> 
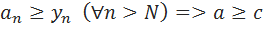
5) 

6) 
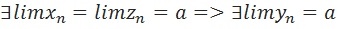
Бесконечно малые (большие) последовательности
Определение.
Последовательность {an} называется бесконечно малой, если существует 
{bn} (bn<>0) называется бесконечно большой, если {  } является бесконечно малой.
} является бесконечно малой.
Определение:
{xn}, {yn} то их суммой, разностью, произведением, отношением называют соответсветствующие {xn+yn}, { xn-yn }, { xnyn }, { xn/yn } (yn<>0)
Теорема!!! {  n} –бм {
n} –бм {  n} – бм, тогда их сумма, разность и произведение является бм последовательностью.
n} – бм, тогда их сумма, разность и произведение является бм последовательностью.
Арифметические свойства последовательности
Теорема!!! 


Док-во: 
{xn} – бм
Теорема!!!

1)  ,
,
2)  ,
,
3) 
Док-во:2)

 |

Монотонные последовательности
Определение.
{an} называется монотонно возрастающей (убывающей), если
an<an+1 (an>an+1)
Определение.
{an} называется монотонно не возрастающей (не убывающей), если an  an+1 (an
an+1 (an 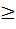 an+1)
an+1)
Какие последовательности называются
Теорема!!! Монотонная ограниченная последовательность имеет предел. Утверждение теоремы следует из существования точной грани, для ограничения множеств.
Определение
{an} имеет предел 
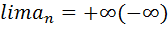
Теорема!!! Неубывающая (не возрастающая) неограниченная последовательность имеет предел 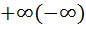
Число Эйлера
Теорема!!!


Фундаментальная последовательность

Теорема!!!(Коши)
Для того чтобы последовательность имела предел необходимо и достаточно, чтобы она была фундаментальной.
Предел функции. Определение предела по Гейне и Коши
Пусть f(x) определена в некоторой (трактованной) проколотой окрестности
 (x0)={x:D<|x-x0|<δ(дельта)}
(x0)={x:D<|x-x0|<δ(дельта)}
Определение 1. (Гейне) Число a называется пределом функции f(x) в точке x0 если ( {xn}) такой, что
{xn}) такой, что
{  =x0, xn<>x0} =>
=x0, xn<>x0} =>  =a
=a
Определение 2 (Каши). Число a является пределом функции f(x) в точке x0, если ( >0) (
>0) ( )
)
( x:0<|x-x0|<
x:0<|x-x0|<  óx
óx  (x0,
(x0,  )) => (|f(x)-a|<
)) => (|f(x)-a|< 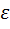 ó f(x)
ó f(x)  (a,
(a, 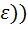
Теорема!!! Определение по Гайне и Коши

Односторонние пределы
Пусть f(x) определена на интервале (x0-c,x0)
Определение. Число a называется пределом функции f(x) в точке x0 при x -> x0 слева (левосторонний предел) если,
Гейне) ( {xn}), xn->x0
{xn}), xn->x0
(xn<x0)

Коши) ( )(
)(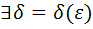 )
)
( x:0<x0-x<
x:0<x0-x<  => |f(x)-a|<
=> |f(x)-a|< 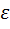
Аналогично вводится правосторонний предел. (Упражнение. Составить определение правостороннего предела)
Теорема!!! Определение односторонних пределов по Гейне и Коши эквивалентны.
Теорема!!! Для того чтобы существовал f(x) в точке необходимо и достаточно, чтобы в этой точке существовали равные между собой односторонние пределы.
Обозначение
a=  (левосторонний предел)
(левосторонний предел)
a=  =f(x0-0) (левосторонний предел)
=f(x0-0) (левосторонний предел)
a= 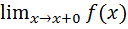 =f(x0+0) (Правосторонний предел)
=f(x0+0) (Правосторонний предел)
Пример 
Основные свойства функции, имеющие предел в точке
1. Если предел существует, то он единственный
2. Если предел существует, то функция ограничена в некоторой окрестности этой точки.
3.  , b<a (b>a), то (
, b<a (b>a), то ( (x0))(
(x0))( 0)) => f(x)>b (f(x)<b))
0)) => f(x)>b (f(x)<b))
4.  =a и (
=a и ( 0))(f(x)
0))(f(x)  => a
=> a 
5. 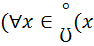 0))
0)) 
( =
=  =a)
=a)
6. Предел сложной функции
Пусть а(ч) определена  0) и
0) и  =y0 , x
=y0 , x  Ʊ(x0) f(x) <>y0
Ʊ(x0) f(x) <>y0
F(y)  (y0)
(y0) 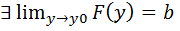 =>
=> 
Теорема!!!
Предел форм и арифметические операции

1. 
2. 
3.  , b<>0
, b<>0
Следствие 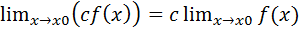
Бесконечно большие и бесконечно малые функции
 является бесконечно мало в x0 (x->x0)
является бесконечно мало в x0 (x->x0)

 – бесконечно мало (б. м.) (x->x0)
– бесконечно мало (б. м.) (x->x0)
Теорема!!! a=  óf(x)-a – бм (x->x0)
óf(x)-a – бм (x->x0)
f(x)в точке х0 равен  если
если
Гейне) ( xn)(xn -> x0; xn<>x0) => f(x0) ->
xn)(xn -> x0; xn<>x0) => f(x0) -> 
Коши) ( (
(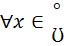 (x0,
(x0, 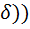 => |f(x)|>M, f(x)>M,
=> |f(x)|>M, f(x)>M,
f(x)<(-M)
f(x) – бб (x->x0)
Замечание. Все эти свойства сформулированы для конечной точки x0 
Упражнение. Сформулировать эти определения x0= 
Теорема!!! Для того чтобы существовал предел при  необходимо и достаточно ó (
необходимо и достаточно ó (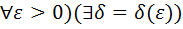
(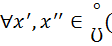 x0,
x0,  |f(x’)-f(x’’)|<
|f(x’)-f(x’’)|< 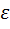
Предел монотонной функции
f(x) определен на интервале a,b называется
1)  x1<x2 => f(x1)<f(x2)
x1<x2 => f(x1)<f(x2)
2) 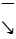 x1
x1  x2 => f(x1)
x2 => f(x1)  f(x2)
f(x2)
3)  x1>x2 => f(x1)>f(x2)
x1>x2 => f(x1)>f(x2)
4) 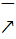 x1
x1 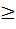 x2 => f(x1)
x2 => f(x1) 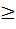 f(x2)
f(x2)
Теорема!!! f(x) является монотонной на интервале (a,b) и ограниченной, т. е. |f(x)|  k, (
k, (
Тогда 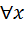 0,
0,  0+0) и
0+0) и  0-0)
0-0)
Неопределенность
При рассмотрении бб и бм последовательностей могут возникать следующие неопределенности

Если он существует, то нахождения называются раскрытием.
Первый замечательный предел



Второй замечательный предел
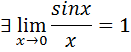
Сравнение функций
f(x) и g(x) определены  0)
0)
 0)
0)
1)|f(x)|<c|g(x)| (c>0)
f(x)=0(g(x)), x  0)
0)
2)f, g – бм x->x0 
f(x)=0(g(x)), x->x0
Пример x3=0(x2), x->0






