Аналитическое выражение для статической характеристики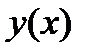 
выводится из системы дифференциальных уравнений, описывающих динамику нашей системы, где все производные приравнены к нулю.
Получим систему уравнений:
Решая данную систему, получим выражение для
Зона нечувствительности равна 0,7
Неравномерность равна 0,03
Выбираем рабочую точку.
Рассмотрим точку со следующими координатами:
время переходного процесса 75с.
Запасы устойчивости по коэффициентам системы.
Также исследование нашей системы можно проводить, изменяя и другие коэффициенты.
При этом коэффициенты 
равны 0,05 и 2 соответственно.
Получаем следующие уравнения для границы устойчивости и предельного цикла:
Плоскость разбиения коэффициентов K1(T1)
Запасы устойчивости по коэффициентам системы: 
, 
.
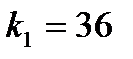Плоскость разбиения коэффициентов K1(T2)
Запасы устойчивости по коэффициентам системы: 
, 
.
Модель программы переходного процесса в системе
Для получения необходимых дифференциальных уравнений построим математическую модель заданной системы:
Тогда система дифференциальных уравнений примет вид:
Текст программы:
procedure TForm1.Button6Click(Sender: TObject);
{переходный процесс и фазовый портрет}
var s1,y1,s,r,r1,k,x,t,y,h,N,y5,k2,k5,x1:real;
i:integer;
const dt=0.001;
y0=0;
s0=0;
r0=0;
begin
k2:=StrToFloat(Edit1.Text);
k5:=StrToFloat(Edit2.Text);
x1:=StrToFloat(Edit6.Text);
t:=0;
Steret;
Chart1.Title.Text.Text:='ïåðåõîäíûé ïðîöåññ';
Chart2.Title.Text.Text:='ôàçîâûé ïîðòðåò';
Chart1.LeftAxis.Title.Caption:='y';
Chart1.BottomAxis.Title.Caption:='t';
s:=s0;
r:=r0;
y:=y0;
repeat
s1:=(-s+k1*(x1-y))/t1;
x:=-k5*y+s;
if (x>0) then
begin
if abs(x)<a then h:=0;
if (x>a) or (x=a) then h:=c*(x-a)/(b-a);
end
else
if (x<-a) or (x=-a) then h:=c*(x+a)/(b-a);
N:=h;
r1:=k2*N;
y1:=(r-y)/t2;
y:=y+y1*dt;
s:=s+s1*dt;
r:=r+r1*dt;
series1.AddXY(t,y);
series3.AddXY(y,y1);
t:=t+dt;
Gauge1.Progress:=round(t/100*100);
until t>100;
end;
Вывод:
В ходе исследования заданной автоматической системы, она будет обладать приемлемым качеством, если принять коэффициенты настройки следующие (рабочая точка)
Приложение
| F(z) |
|
|
|
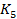
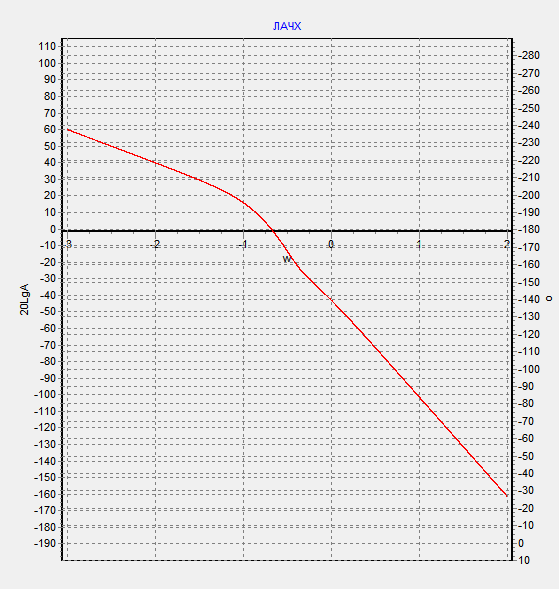
Передаточная функция:
Система обладает фильтром низких частот
Плоскость разбиения коэффициентов Т2(T1)
Запасы устойчивости по коэффициентам системы: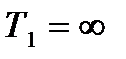 
, 
.
Плоскость разбиения коэффициентов K5(T1)
Запасы устойчивости по коэффициентам системы: ,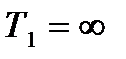 
.
