Если в точке 
нарушено условие непрерывности и односторонние пределы конечны, то она называется точкой разрыва первого рода.
Начнём с самого оптимистичного случая. По первоначальной задумке урока я хотел рассказать теорию «в общем виде», но чтобы продемонстрировать реальность материала, остановился на варианте с конкретными действующими лицами.
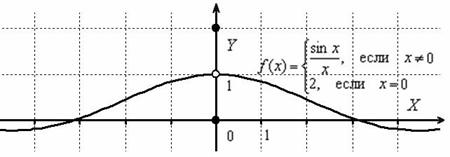
Уныло, как фото молодожёнов на фоне Вечного огня, но нижеследующий кадр общепринят. Изобразим на чертеже график функции 
:
Данная функция непрерывна на всей числовой прямой, кроме точки 
. И в самом деле, знаменатель же не может быть равен нулю. Однако в соответствии со смыслом предела – мы можем бесконечно близко приближаться к «нулю» и слева и справа, то есть, односторонние пределы существуют и, очевидно, совпадают:
(Условие №2 непрерывности выполнено).
Но функция не определена в точке , следовательно, нарушено Условие №1 непрерывности, и функция терпит разрыв в данной точке.
Разрыв такого вида (с существующим общим пределом) называют устранимым разрывом. Почему устранимым? Потому что функцию можно доопределить в точке разрыва:
Странно выглядит? Возможно. Но такая запись функции ничему не противоречит! Теперь разрыв устранён и все счастливы:
Выполним формальную проверку:
1) 
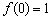– функция определена в данной точке;
2) – общий предел существует;
3) 
– предел функции в точке равен значению данной функции в данной точке.
Таким образом, все три условия выполнены, и функция непрерывна в точке по определению непрерывности функции в точке.
Впрочем, ненавистники матана могут доопределить функцию нехорошим способом, например 
:
Любопытно, что здесь выполнены первые два условия непрерывности:
1) 
– функция определена в данной точке;
2) – общий предел существует.
Но третий рубеж не пройден: 
, то есть предел функции в точке не равен значению данной функции в данной точке.
Таким образом, в точке функция терпит разрыв.
Второй, более грустный случай носит название разрыва первого рода со скачком. А грусть навевают односторонние пределы, которые конечны и различны. Пример изображён на втором чертеже урока. Такой разрыв возникает, как правило, в кусочно-заданных функциях, о которых уже упоминалось в статье о преобразованиях графиков.
Рассмотрим кусочную функцию 
и выполним её чертёж. Как построить график? Очень просто. На полуинтервале 
чертим фрагмент параболы 
(зеленый цвет), на интервале 
– отрезок прямой 
(красный цвет) и на полуинтервале 
– прямую 
(синий цвет).
При этом в силу неравенства 
значение 
определено для квадратичной функции (зелёная точка), и в силу неравенства 
, значение 
определено для линейной функции (синяя точка):
В самом-самом тяжёлом случае следует прибегнуть к поточечному построению каждого куска графика (см. первый урок о графиках функций).
Сейчас нас будет интересовать только точка 
. Исследуем её на непрерывность:
1) 
– функция определена в данной точке.
2) Вычислим односторонние пределы.
Слева у нас красный отрезок прямой, поэтому левосторонний предел: 
Справа – синяя прямая, и правосторонний предел: 
В результате получены конечные числа, причем они не равны. Поскольку односторонние пределы конечны и различны: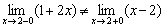 
, то наша функция терпит разрыв первого рода со скачком.
Логично, что разрыв не устраним – функцию действительно не доопределить и «не склеить», как в предыдущем примере.
