Задания для выполнения самостоятельных работ

СОДЕРЖАНИЕ

Введение………………………………………………………………………………………

1 Распределение видов и объема внеаудиторной самостоятельной работы между разделами дисциплины Математика………………………………………………………….

2 Задания для выполнения внеаудиторных самостоятельных работ……………………………………………………………………………………………….

3 Внеаудиторные контрольные работы………………………………………….........................

4 Список литературы……………………………………………………………………………...

 

ВВЕДЕНИЕ

Методические указания для организации внеаудиторной самостоятельной работы обучающихся по дисциплине Математика составлены в соответствии с ФГОС, учебным планом и рабочей программой учебной дисциплины входящей в состав образовательной программы специальности 23.02.04 Техническая эксплуатация подъемно-транспортных, строительных, дорожных машин и оборудования (по отраслям).

Дисциплина Математика входит в математический и общий естественнонаучный учебный цикл образовательной программы.

Целью методических указаний является организация внеаудиторной самостоятельной работы обучающихся по данной дисциплине.

В настоящее время актуальным становятся требования к личным качествам современного обучающегося – умению самостоятельно пополнять и обновлять знания, вести самостоятельный поиск необходимого материала, быть творческой личностью. Ориентация учебного процесса на саморазвивающуюся личность делает невозможным процесс обучения без учета индивидуально-личностных особенностей обучаемых, предоставления им права выбора путей и способов обучения. Появляется новая цель образовательного процесса – воспитание личности, ориентированной на будущее, способной решать типичные проблемы и задачи исходя из приобретенного учебного опыта и адекватной оценки конкретной ситуации.

Решение этих задач требует повышения роли самостоятельной работы обучающихся над учебным материалом, усиления ответственности преподавателя за развитие навыков самостоятельной работы, за стимулирование профессионального роста студентов, воспитание их творческой активности и инициативы.

Выполнение обучающимися внеаудиторной самостоятельной работы способствует формированию общих и профессиональных компетенций:

ОК 1 Понимать сущность и социальную значимость своей будущей профессии, проявлять к ней устойчивый интерес.

ОК 2 Организовывать собственную деятельность, выбирать типовые методы и способы выполнения профессиональных задач, оценивать их эффективность и качество.

ОК 3 Принимать решения в стандартных и нестандартных ситуациях и нести за них ответственность.

ОК 4 Осуществлять поиск и использование информации, необходимой для эффективного выполнения профессиональных задач, профессионального и личностного развития.

ОК 5 Использовать информационно-коммуникационные технологии в профессиональной деятельности.

ОК 6 Работать в коллективе и команде, эффективно общаться с коллегами, руководством, потребителями.

ОК 7 Брать на себя ответственность за работу членов команды (подчиненных), результат выполнения заданий.

ОК 8 Самостоятельно определять задачи профессионального и личностного развития, заниматься самообразованием, осознанно планировать повышение квалификации.

ОК 9 Ориентироваться в условиях частой смены технологий в профессиональной деятельности.

ПК 1.3Выполнять требования нормативно-технической документации по организации эксплуатации машин при строительстве, содержании и ремонте дорог.

ПК 2.3 Определять техническое состояние систем и механизмов подъемно-транспортных, строительных, дорожных машин и оборудования.

ПК 2.4 Вести учетно-отчетную документацию по техническому обслуживанию и ремонту подъемно-транспортных, строительных, дорожных машин и оборудования.

ПК 3.3 Составлять и оформлять техническую и отчетную документацию о работе ремонтно-механического отделения структурного подразделения.

ПК 3.4 Участвовать в подготовке документации для лицензирования производственной деятельности структурного подразделения.

Количество часов на освоение рабочей программы учебной дисциплины:

максимальной учебной нагрузки обучающегося 96 часа, в том числе:

обязательной аудиторной учебной нагрузки обучающегося 64 часов;

самостоятельной работы обучающегося 32 часов.

В структуру методических указаний входит: распределение видов и объема внеаудиторной самостоятельной работы между разделами дисциплины, задания для самостоятельной работы, внеаудиторные контрольные работы, список литературы.

 

РАСПРЕДЕЛЕНИЕ ВИДОВ И ОБЪЕМА ВНЕАУДИТОРНОЙ САМОСТОЯТЕЛЬНОЙ РАБОТЫ МЕЖДУ РАЗДЕЛАМИ ДИСЦИПЛИНЫ МАТЕМАТИКА

Согласно ППССЗ дисциплины Математика на внеаудиторную самостоятельную работу студента отводится 32 часа.

 

Раздел дисциплины	Объем часов на раздел	Вид ВСР	Объем ВСР (час)
Раздел 1 Комплексные числа		1 Проработка конспекта занятия, учебных изданий. 2 Контрольная работа №1 по разделу: задания 1-5 по десяти вариантам.
Раздел 2 Основы дискретной математики		1 Проработка конспекта занятия, учебных изданий. 2 Контрольная работа №2 по разделу: задания 1-5 по десяти вариантам.
Раздел 3 Математический анализ		1 Проработка конспекта занятия, учебных изданий и дополнительной литературы. 2 Решение задач по теме «Исследование функции и построение графика с помощью производной». 3 Решение задач по теме «Вычисление площадей плоских фигур». 4 Решение задач по теме«Дифференциальные уравнения». 5 Решение задач по теме «Признаки сходимости числовых рядов». 4 Контрольная работа №3 по разделу: задания 1-5 по десяти вариантам.
Раздел 4 Основы теории вероятности и математической статистики		1 Проработка конспекта занятия, учебных изданий и дополнительной литературы. 2 Решение задач по теме «Теоремы сложения и умножения вероятностей». 3 Контрольная работа №4 по разделу: задания 1-5 по десяти вариантам.
Раздел 5 Основные численные методы		1 Проработка конспекта занятия, учебных изданий и дополнительной литературы. 2 Решение задач по теме «Формулы численного интегрирования». 3 Решение задач по теме «Формулы приближенного дифференцирования».
Общий объем аудиторных часов по дисциплине		Общий объем ВСР

 

ЗАДАНИЯ ДЛЯ ВЫПОЛНЕНИЯ САМОСТОЯТЕЛЬНЫХ РАБОТ

Самостоятельные работы выполняются индивидуально в свободное от занятий время.

Обучающийся обязан:

- перед выполнением самостоятельной работы, повторить теоретический материал, пройденный на аудиторных занятиях;

- выполнить работу согласно заданию;

- по каждой самостоятельной работе представить преподавателю отчет в виде письменной работы.

При выполнении самостоятельных работ обучающийся должен сам принять решение об оптимальном использовании возможностей программного обеспечения. Если по ходу выполнения самостоятельной работы у обучающегося возникают вопросы и затруднения, он может консультироваться у преподавателя. Каждая работа оценивается по пятибалльной системе.

Самостоятельная работа по теме «Исследование функции с помощью производной и построение графика».

Цель работы:отработка навыков исследования функции с помощью производной и построение графика.

Задание:

1 Повторите общую схему исследования функции с помощью производной и построение графика.

2 Исследуйте функцию с помощью производной и постройте её график (индивидуальное задание 30 вариантов).

1)

2)

3)

4)

5)

6)

7)

8)

9)

10)

11)

12)

13)

14)

15)

16)

17)

18)

19)

20)

21)

22)

23)

24)

25)

26)

27)

28)

29)

30)

Самостоятельная работа по теме «Вычисление площадей плоских фигур».

Цель работы:отработка навыков вычисление площадей плоских фигур.

Задание:

1 Повторите геометрический смысл определенного интеграла и формулу Ньютона-Лейбница.

2 Вычислите площадь фигуры, ограниченной линиями (индивидуальное задание 30 вариантов).

1)

2)

3)

4)

5)

6)

7)

8)

9)

10)

11)

12)

13)

14)

15)

16)

17)

18)

19)

20)

21)

22)

23)

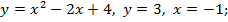
24)

25)

26)

27)

28)

29)

30)

Самостоятельная работа по теме «Дифференциальные уравнения».

Цель работы:отработка навыков решения дифференциальных уравнений.

Задание:

1 Повторите способы решения дифференциальных уравнений с разделяющими переменными и линейных однородных уравнений второго порядка с постоянными коэффициентами.

2 Решите дифференциальные уравнения.

5)

6)

7)

8)

Самостоятельная работа по теме «Признаки сходимости числовых рядов».

Цель работы:отработка навыков определения сходимости рядов.

Задание:

1 Повторите признаки сходимости числовых рядов.

2 Исследуйте ряд на сходимость.

1)

2)

3)

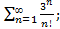
4)

5)

6)

Самостоятельная работа по теме «Теоремы сложения и умножения вероятностей».

Цель работы:отработка навыков решения задач по теории вероятности.

Задание:

1 Повторите теоретический материал по теме «Теоремы сложения и умножения вероятностей».

2 Решите задачи.

1) Катя и Аня пишут диктант. Вероятность того, что Катя допустит ошибку, составляет 60%, а вероятность ошибки у Ани составляет 40%. Найти вероятность того, что обе девочки напишут диктант без ошибок.

2) Завод выпускает 15% продукции высшего сорта, 25% - первого сорта, 40% - второго сорта, а все остальное – брак. Найти вероятность того, что выбранное изделие не будет бракованным.

3) Каждый из трех стрелков стреляет в мишень по одному разу, причем попадания первого стрелка составляет 90%, второго – 80%, третьего – 70%. Найдите вероятность того, что все три стрелка попадут в мишень?

4) В корзине лежат фрукты, среди которых 30% бананов и 60% яблок. Какова вероятность того, что выбранный наугад фрукт будет бананом или яблоком?

Самостоятельная работа по теме «Формулы численного интегрирования».

Цель работы:отработка навыков вычисления определенного интеграла с помощью формул численного интегрирования.

Задание:

1 Повторите формулы численного интегрирования.

2 Вычислите по формуле прямоугольников и трапеций определенный интеграл, разбив интервал интегрирования на десять равных частей. Значения функции вычислите с точностью до .

1)

2)

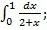
3)

Самостоятельная работа по теме «Формулы приближенного дифференцирования».

Цель работы:отработка навыков нахождения производной с помощью формул численного дифференцирования.

Задание:

1 Повторите формулы численного дифференцирования.

2 Найдите значения первой и второй производных функций, заданной таблично, в точках :

1)

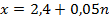
x	2,4	2,6	2,8	3,0	3,2	3,4
y(x)	3,526	3,782	3,945	4,043	4,104	4,155

а) ; б) ; в) ; г) .

2)

x	3,6	3,8	4,0	4,2	4,4	4,6
y(x)	4,222	4,331	4,507	4,775	5,159	5,683

а) ; б) ; в) ; г) .

ДОМАШНИЕ КОНТРОЛЬНЫЕ РАБОТЫ

Система оценивания:

− оценка "5" ставится, если работа выполнена полностью, без ошибок или содержит не более двух недочетов;

− оценка "4" ставится, если работа выполнена полностью, содержит одну грубую ошибку или не более 3-4 недочетов;

− оценка "3" ставится, если работа выполнена полностью, содержит две грубые ошибки или не более 5-6 недочетов;

− оценка "2" ставится во всех остальных случаях.

К грубым ошибкам относятся ошибки, которые обнаруживают незнание формул, правил, основных свойств, теорем и неумение их применять, незнание приемов решения задач, а также вычислительные ошибки, если они не являются опиской.

К недочетам относятся: нерациональное решение, описки, недостаточность; отсутствие пояснений, обоснований в решениях.

Если одна и та же ошибка (один и тот же недочет) встречаются несколько раз, то это рассматривается как одна ошибка (один недочет).

При выполнении контрольных работ необходимо строго придерживаться указанных ниже правил. Работы, выполненные без соблюдения этих правил не зачитываются и возвращаются обучающемуся для переработки.

1 Контрольная работа должна быть выполнена в тетради для домашних контрольных работ в клетку чернилами любого цвета, кроме красного.

2 В заголовке на обложке тетради должны быть ясно написаны название дисциплины, фамилия студента и его инициалы, номер группы, номер варианта.

3 В работу должны быть включены все задания строго по положенному варианту. Контрольные работы содержащие задания не своего варианта не зачитываются.

4 Решения заданий надо располагать в порядке возрастания их номеров.

5 Перед решением каждой задачи надо полностью вписать ее условие.

6 Решения задач следует излагать подробно и аккуратно, объясняя и мотивируя все действия по ходу решения.

7 В каждой домашней контрольной работе по пять заданий, каждое из которых содержит по десять задач. Ниже приводится таблица 1 с номерами задач, входящих в контрольные работы в соответствии с вариантом.

Таблица 1

Номер варианта	Номер задания

 

Контрольная работа №1

Комплексные числа

1-10 Выполните сложение, вычитание, умножение и деление комплексных чисел в алгебраической форме.

1)

2)

3)

4)

5)

6)

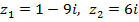
7)

8)

9)

10)

11-20 Изобразить на плоскости число и найти его модуль.

11)

12)

13)

14)

15)

16)

17)

18)

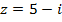
19)

20)

21-30 Найти тригонометрическую и показательную формы комплексного числа.

21)

22)

23)

24)

25)

26)

27)

28)

29)

30)

31-40 Вычислить.

31)

32)

33)

34)

35)

36)

37)

38)

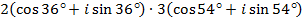
39)

40)

41-50 Вычислить, пользуясь формулой Муавра.

41)

42)

43)

44)

45)

46)

47)

48)

49)

50)

Контрольная работа №2

Основы дискретной математики

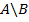1-10 Осуществить над множествами операции: а) ; б) ; в) ; г) .

1)

2)

3)

4)

5)

6)

7)

8)

9)

10)

11-20 Найти: .

11)

12)

13)

14)

15)

16)

17)

18)

19)

20)

21-30 С помощью диаграммы Эйлера-Венна изобразить множество.

21)

22)

23)

24)

25)

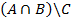
26)

27)

28)

29)

30)

31-40 Решите задачу с использованием диаграммы Эйлера-Венна.

31) Четырнадцать спортсменов участвовали в кроссе, 16 – в соревнованиях по плаванию, 10 – в велосипедных гонках. Восемь участников участвовали в кроссе и заплыве, 4 – в кроссе и велосипедных гонках, 9 – в плавании и велосипедных гонках. Во всех трех соревнованиях участвовали три человека. Сколько всего было спортсменов?

32) В туристском клубе несколько раз за лето организуются походы, причем все члены клуба хотя бы раз в них участвуют. Сорок человек побывали в пеших походах, 28 – в конных, 25 – в лодочных. И в пеших, и в конных походах побывало 20 человек, в пеших и лодочных – 15, в конных и лодочных – 8, во всех видах походов побывало 6 человек. Сколько туристов в клубе?

33) В отделе НИИ работают несколько человек, причем каждый из них знает хотя бы один иностранный язык. Английский язык знают шесть человек, немецкий – шесть человек, французский – семь. Четыре человека знают английский и немецкий языки, три человека – немецкий и французский, два – 18 французский и английский, один знает все три языка. Сколько человек работает в отделе?

34) Из 80 студентов занимаются баскетболом 30 человек, легкой атлетикой 25 человек, шахматами - 40 человек. Баскетболом и легкой атлетикой занимается 8 человек, шахматами и легкой атлетикой – 10 человек, шахматами и баскетболом – 5 человек. Тремя видами спорта занимаются три человека. Сколько человек занимаются спортом?

35) Десять читателей взяли в библиотеке фантастику, 11 – детективы, 8 – приключения. Фантастику и приключения взяли 4 человека, фантастику и детективы – 6, приключения и детективы – 3, двое взяли три вида книг. Сколько читателей побывало в библиотеке?

36) Из 10 участников ансамбля шестеро умеют играть на гитаре, пятеро на ударных инструментах, пятеро на духовых. Двумя инструментами владеют: гитарой и ударными – трое, ударными и духовыми – двое, гитарой и духовыми – четверо. Остальные участники ансамбля только поют. Сколько певцов в ансамбле?

37) Каждый из студентов группы занимается хотя бы одним видом спорта. Пятеро занимаются альпинизмом, шестеро – волейболом, 10 человек – борьбой. Известно, что двое занимаются и альпинизмом, и волейболом; трое – волейболом и борьбой; четверо – альпинизмом и борьбой; а один занимается всеми тремя видами спорта. Сколько студентов занимается только борьбой?

38) В одной из студенческих групп все студенты умеют программировать. Десять человек умеют работать на Бейсике, 10 – на Паскале, 6 – на Си. Два языка знают: 6 человек Бейсик и Паскаль, 4 – Паскаль и Си, 3 – Бейсик и Си. Один человек знает все три языка. Сколько студентов в группе?

39) При изучении читательского спроса оказалось, что 60% опрошенных читает журнал «Огонек», 50% – журнал «Юность», 50% - журнал «Аврора». 19 Журналы «Огонек» и «Юность» читают 30% опрошенных, «Юность» и «Аврора» – 20%, «Огонек» и «Аврора» – 40%, все три журнала – 10%. Сколько процентов опрошенных не читают ни один журнал?

40) В день авиации всех желающих катали на самолете, планере, дельтаплане. На самолете прокатилось 30 человек, на планере – 20, на дельтаплане – 15. И на самолете, и на планере каталось 10 человек, на самолете и дельтаплане – 12, на планере и дельтаплане – 5, два человека прокатились и на самолете, и на планере, и на дельтаплане. Сколько было желающих прокатиться?

41-50 Определить степени вершин графа.

41)

42)

 

43)

44)

45)

46)

 

47)

48)

49)

50)

 

Контрольная работа №3

Математический анализ

1-10 Найти производную данной функции.

1)

2)

3)

4)

5)

6)

7)

8)

9)

10)

11-20 Вычислите определенный интеграл.

11)

12)

13)

14)

15)

16)

17)

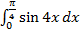
18)

19)

20)

21-30 Найдите общее решение дифференциального уравнения первого порядка.

21)

22)

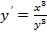
23)

24)

25)

26)

27)

28)

29)

30)

31-40 Найдите общее решение дифференциального уравнения второго порядка.

31)

32)

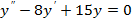
33)

34)

35)

36)

37)

38)

39)

40)

41-50 Исследовать на сходимость ряд.

41)

42)

43)

44)

45)

46)

47)

48)

49)

50)

 

Контрольная работа №4

Основы теории вероятности и математической статистики

1-10 Вычислить значения выражений.

1)

2)

3)

4)

5)

6)

7)

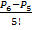
8)

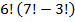
9)

10)

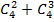
11-20 Решить задачу, используя формулы комбинаторики.

11) Сколько различных 5-значных чисел, все цифры которых различны можно записать с помощью цифр 4, 5, 6, 7, 8?

12) На склад завезли 17 серверов с различными дефектами, которые стоят в 2 раза дешевле нормальных серверов. Директор купил в школу 14 таких серверов. Сколькими способами директор может выбрать бракованные серверы?

13) Научное общество состоит из 25 человек. На ближайшем собрании необходимо выбрать президента общества, вице-президента, ученого секретаря и казначея. Сколькими способами может быть сделан этот выбор, если каждый член общества может занимать лишь один пост?

14) Сколькими способами можно выбрать 6 разных пирожных в кондитерской, где есть 11 разных сортов пирожных?

15) Сколькими способами могут быть присуждены 1-я, 2-я и 3-я премии трем лицам, если число соревнующихся равно 10?

16) У мамы есть один апельсин, одна груша, одно яблоко и один банан. Она хочет раздать их четверым детям так, чтобы каждому достался какой-нибудь фрукт. Сколько имеется вариантов это сделать?

17) У Артоса, Портоса и Арамиса на всех имеется одна шпага, один кинжал и один пистолет. Сколько у них способов распределить оружие так, чтобы все были вооружены?

18) Сколькими способами из 10 спортсменов можно отобрать команду из 6 человек?

19) Сколькими способами из восьми человек можно избрать комиссию, состоящую из пяти членов?

20) На выборах победили 9 человек - Сафонов, Николаев, Петров, Кулаков, Мишин, Гусев, Володин, Афонин, Титов. Из них нужно выбрать председателя, заместителя и профорга. Сколькими способами это можно сделать?

21-30 Решить задачу, используя классическое определение вероятности.

21) В ящике с деталями оказалось 300 деталей 1 сорта, 200 деталей 2 сорта и 50 деталей 3 сорта. Наудачу вынимают одну из деталей. Чему равна вероятность вынуть деталь: а) 1 сорта; б) 2 сорта; в) 3 сорта?

22) В урне находятся 20 белых и 15 черных шаров. Наудачу вынимают один шар, который оказался белым, и откладывают его в сторону. После этого берут еще один шар. Найдите вероятность того, что этот шар окажется белым.

23) В урне находятся 7 белых и 5 черных шаров. Найдите вероятность того, что: 1) наудачу вынутый шар окажется черным; 2) два наудачу вынутых шара окажутся черными.

24) Считая выпадение любой грани игральной кости одинаково вероятным, найдите вероятность выпадения грани с нечетным числом очков.

25) В коробке имеются 30 лотерейных билетов, из которых 26 пустых (без выигрышей). Наугад вынимают одновременно 4 билета. Найдите вероятность того, что из 4 билетов два окажутся выигрышными.

26) Наудачу выбрано натуральное число, не превосходящее 10. Какова вероятность того, что это число является простым?

27) На странице книги имеется 2500 букв. Буква «а» встречается 190 раз. Какова вероятность того, что случайно выбрана буква не есть буква «а»?

28) В партии из 23 деталей находятся 10 бракованных. Вынимают из партии наудачу две детали. Какова вероятность того, что обе детали окажутся бракованными?

29) На каждой из пяти одинаковых карточек напечатана одна из следующих букв: «а», «м», «р», «т», «ю». Карточки тщательно перемешаны. Найти вероятность того, что на четырех вынутых по одной карточке можно прочесть слово «юрта».

30) В лотерее из 1500 билетов имеются 300 выигрышных. Вынимают наугад один билет. Чему равна вероятность того, что этот билет выигрышный?

31-40 Решить задачу, используя формулу Бернулли.

31) Из 100 аккумуляторов за год хранения 7 выходит из строя. Наудачу выбирают 5 аккумуляторов. Определить вероятность того, что среди них 3 исправных.

32) Вероятность выпуска бракованного изделия на станке равна 0,2. Определить вероятность того, что в партии из десяти выпущенных на данном станке деталей ровно 10 будут без брака.

33) В четырех попытках разыгрываются некоторые предметы. Вероятность выигрыша в каждой попытке известна и равна 0,5. Какова вероятность выигрыша ровно трех предметов?

34) Вероятность попадания в цель при одном выстреле равна 0,6. Какова вероятность того, что 8 выстрелов дадут 5 попаданий?

35) Найти вероятность наступления события A ровно 3 раза в 5 независимых испытаниях, если вероятность появления этого события в каждом испытании равна 1/3.

36) В магазине 5 холодильников. Вероятность выхода из строя каждого холодильника в течение года равна 0,2. Найти вероятность того, что в течение года ремонта потребует 4 холодильника.

37) Вероятность попадания при одном выстреле 0,9. Определить вероятность того, что при 6 наудачу сделанных выстрелах будет 4 попадания.

38) Всхожесть семян оценивается вероятностью 0,8. Какова вероятность того, что из пяти посеянных семян взойдет три?

39) Вероятность попадания в цель при одном выстреле составляет 0,8.Найдите вероятность трех попаданий при четырех выстрелах.

40) При обработке деталей на станке в среднем 4% из них бывают с дефектами. Какова вероятность того, что каждые две детали из 30 взятых на проверку окажутся с дефектами?

41-50 Найти математическое ожидание и дисперсию случайной величины X, зная закон ее распределения.

41)

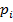
	0,1	0,4	0,5

42)

	0,1
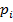
	0,4	0,2	0,15	0,25

43)

	-1
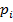
	0,48	0,01	0,09	0,42

44)

	-1
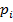
	0,19	0,51	0,25	0,05

45)

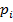
	0,1	0,6	0,3

46)

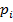
	0,1	0,6	0,3

47)

	-1
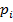
	0,1	0,3	0,4	0,2

48)

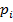
	0,3	0,1	0,2	0,4

49)

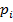
	0,2	0,4	0,3	0,08	0,02

50)

	-2	-1
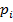
	0,6	0,1	0,1	0,2

 

СПИСОК ЛИТЕРАТУРЫ

1 Григорьев В.П. Элементы высшей математики: учебник для студ. учреждений сред. проф. образования / В.П. Григорьев, Ю.А. Дубинский. – 6-е изд., стер. – М.: Издательский центр «Академия», 2011.

2 Дадаян А.А. Математика: учебник. – 3-е изд. – М.: ФОРУМ, 2011.

3 Омельченко В.П., Курбатова Э.В. Математика: учеб. пособие - Изд. 3-е, испр. – Ростов н/Д: Феникс, 2013. – 380с. – (Среднее профессиональное образование).