Возрастание и убывание функции
1. Необходимое условие.
Определение 1. Если дифференцируемая на интервале  функция
функция  возрастает, то ее производная
возрастает, то ее производная  остается неотрицательной на этом интервале:
остается неотрицательной на этом интервале:
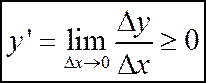
Определение 2. Если дифференцируемая на интервале  функция
функция  убывает, то ее производная остается не положительной:
убывает, то ее производная остается не положительной:

2. Достаточное условие.
Определение 3. Если функция на интервале  в каждой точке имеет положительную производную, то функция на этом интервале возрастает.
в каждой точке имеет положительную производную, то функция на этом интервале возрастает.
Определение 4. Если функция в каждой внутренней точке интервала  имеет отрицательную производную, то функция убывает на этом интервале.
имеет отрицательную производную, то функция убывает на этом интервале.
Экстремумы функции

Определение 1. Точки, в которых производная данной функции равна нулю или не существует, называются критическими.
Первый достаточный признак существования экстремума
Определение 1. Если непрерывная функция  имеет производную во всех внутренних точках интервала
имеет производную во всех внутренних точках интервала  , содержащем критическую точку
, содержащем критическую точку  , и при переходе слева направо через критическую точку производная меняет знак, то в этой точке существует экстремум:
, и при переходе слева направо через критическую точку производная меняет знак, то в этой точке существует экстремум:
1). Если знак меняется с (+) на (-), то в этой точке  .
.
2). Если знак меняется с (-) на (+), то в этой точке  .
.
Второй достаточный признак существования экстремума
Определение 1. Если в точке  производная равна нулю
производная равна нулю  ,
,  - существует и не равна нулю, то, если:
- существует и не равна нулю, то, если:
 - то функция имеет
- то функция имеет  ;
;
 - то функция имеет
- то функция имеет 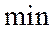 .
.

Замечание.
Если  в критической точке обращается в ноль или не существует, вторым достаточным признаком пользоваться нельзя и следует перейти к 1-му достаточному признаку.
в критической точке обращается в ноль или не существует, вторым достаточным признаком пользоваться нельзя и следует перейти к 1-му достаточному признаку.
Выпуклость и вогнутость графика функции

Определение 1. График дифференцируемой функции  называется выпуклым, если он расположен ниже любой своей касательной.
называется выпуклым, если он расположен ниже любой своей касательной.
Определение 2. График дифференцируемой функции  называется вогнутым, если он расположен выше любой своей касательной.
называется вогнутым, если он расположен выше любой своей касательной.
Достаточный признак выпуклости (вогнутости) графика функции.
Определение 3. Если для дважды дифференцированной функции  на интервале
на интервале 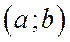 :
:
а)  во всех точках интервала, то график функции выпуклый на этом интервале;
во всех точках интервала, то график функции выпуклый на этом интервале;
б)  - то график вогнутый.
- то график вогнутый.
Определение 4. Точки графика непрерывной функции  , отделяющие выпуклую часть от вогнутой, называют точками перегиба.
, отделяющие выпуклую часть от вогнутой, называют точками перегиба.
Пусть в некоторой точке  функция
функция  непрерывна и, если при переходе через точку
непрерывна и, если при переходе через точку 
 меняет знак, то график функции в точке
меняет знак, то график функции в точке  имеет точку перегиба.
имеет точку перегиба.
Необходимое условие существования точки перегиба.
Точки перегиба следует искать только среди таких, в которых вторая производная обращается в ноль или не существует.
Асимптоты графика функции
Определение 1. Прямая называется асимптотой для кривой, если расстояние от текущей точки М этой кривой до прямой стремится к нулю, при неограниченном удалении точки М от начала координат.
Асимптоты бывают:
1) вертикальные;
2) наклонные;
3) горизонтальные.
1. Наклонные асимптоты (их не более двух).
Уравнения наклонных асимптот ищут в виде  ,
,
где  ;
;  .
.
2. Если  =>
=>  - горизонтальная асимптота
- горизонтальная асимптота
Вертикальные асимптоты.
Если функция  имеет точки разрыва, то график этой функции имеет вертикальные асимптоты.
имеет точки разрыва, то график этой функции имеет вертикальные асимптоты.
Определение 2. Прямая 
 является вертикальной асимптотой графика функции
является вертикальной асимптотой графика функции  , если
, если

Пример. Найти асимптоты графика функции  .
.
Прямая х = -2 является вертикальной асимптотой кривой.
Найдем наклонные асимптоты.


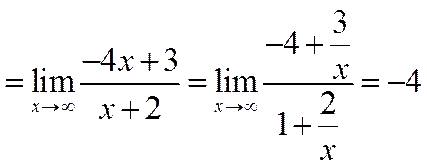
Итого, прямая у = х – 4 является наклонной асимптотой.

Общая схема исследования функции
1. Область определения функции, точки разрыва, вертикальные асимптоты.
2. Нули функции (точки пересечения графика с осями координат).
3. Четность и нечетность функции (симметрия графика).
4. Наклонные и горизонтальные асимптоты.
5. Интервалы возрастания и убывания функции, экстремум функции.
6. Интервалы выпуклости и вогнутости графика функции, точки перегиба.
7. Эскиз графика функции.
Пример: Провести полное исследование функции  и построить ее график.
и построить ее график.
1. 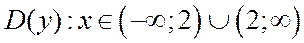 .
.
 - точка разрыва, следовательно
- точка разрыва, следовательно  - уравнение вертикальной асимптоты.
- уравнение вертикальной асимптоты.
2. Точки пересечения



3.
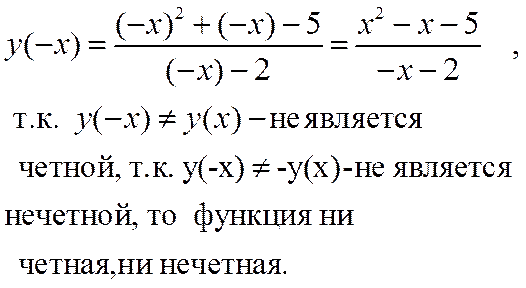
4. Найдем асимптоты графика функции, воспользовавшись уравнением 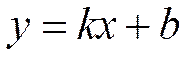
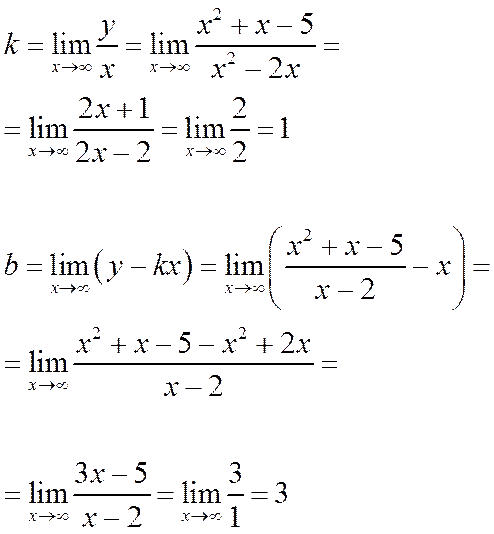
 - уравнение наклонной асимптоты.
- уравнение наклонной асимптоты.
5.




 - критические точки,
- критические точки,  не существует при
не существует при  .
.
| х | 
| 
| 
| 
| |||

| + | - | не сущ. | - | + | ||
| у | 
| 
| не сущ. | 
| 
| ||

| 
|

6.

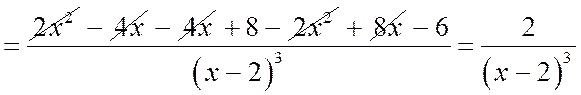

| х | 
| 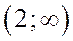
| |

| - | не сущ. | + |
| у | 
| не сущ. | 
|
| перегиб |

7.
Построим график функции:

§21. Наименьшее и наибольшее значение функции  на отрезке
на отрезке
Правило нахождения.
1) Находим критические точки, входящие в отрезок  .
.
2) Вычисляем значения функции в критических точках и на концах отрезка.
3) Из всех значений выбираем наименьшее и наибольшее.
Пример: Найти наибольшее и наименьшее значения функции  .
.
1) 
 .
.
2) 



 .
.
3).  -наибольшее значение
-наибольшее значение


 - наименьшее значение.
- наименьшее значение.






