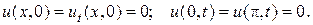
1. 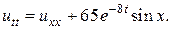 2.
2. 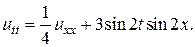
3. 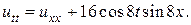 4.
4. 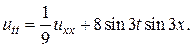
5. 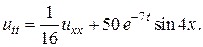 6.
6. 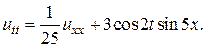
7. 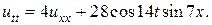 8.
8. 
9.  10.
10. 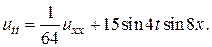
11.  12.
12. 
13. 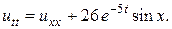 14.
14. 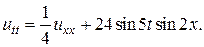
15. 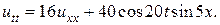 16.
16. 
17.  18.
18. 
19.  20.
20. 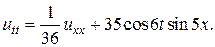
21.  22.
22. 
23. 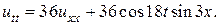 24.
24. 
25. 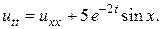 26.
26. 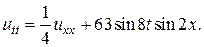
27.  28.
28. 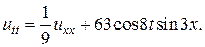
29.  30.
30. 
31. 
11.4. Справочный материал:
1) Задача Штурма-Лиувилля:
- дифференциальное уравнение 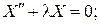
- граничные условия 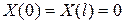 .
.
Разыскиваются значение параметра  (собственные числа), при которых существуют ненулевые решения дифференциального уравнения, удовлетворяющие граничным условиям, а также и сами ненулевые решения (собственные функции).
(собственные числа), при которых существуют ненулевые решения дифференциального уравнения, удовлетворяющие граничным условиям, а также и сами ненулевые решения (собственные функции).
Рассматриваются и задачи Штурма-Лиувилля с граничными условиями вида
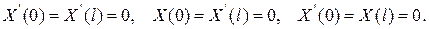
2) Смешанная задача для волнового уравнения на отрезке 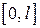 c однородными граничными условиями:
c однородными граничными условиями:
- дифференциальное уравнение 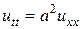 ;
;
- начальные условия 
-граничные условия 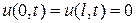 .
.
Рассматриваются также однородные граничные условия следующих видов:

Решение этой задачи по методу Фурье получается в виде
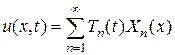
где 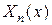 - собственные функции задача Штурма-Лиувилля с условиями, соответствующими рассматриваемым граничным условиям;
- собственные функции задача Штурма-Лиувилля с условиями, соответствующими рассматриваемым граничным условиям;
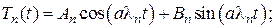
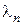 - собственные числа задачи Штурма-Лиувилля;
- собственные числа задачи Штурма-Лиувилля;  ,
,  - коэффициенты, определяемые по начальным условиям.
- коэффициенты, определяемые по начальным условиям.
3) Смешанная задача для неоднородного волнового уравнения
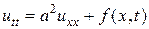
Ее решение можно получить в виде разложения по собственным функциям задачи Штурма-Лиувилля

где 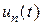 - решения задачи Коши
- решения задачи Коши
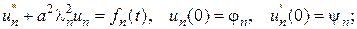
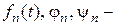 коэффициенты разложений
коэффициенты разложений
 ,
, 
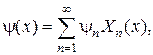
4) Смешанная задача для уравнения теплопроводности на отрезке 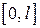 с однородными граничными условиями:
с однородными граничными условиями:
- дифференциальное уравнение  ;
;
- начальное условие 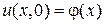
- граничные условия 
или одно из
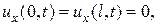
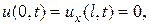
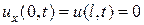
Решение этой задачи по методу Фурье получается в виде
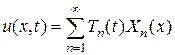 ,
,
где 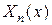 - собственные функции задачи Штурма – Лиувилля с условиями, соответствующими рассматриваемым граничным условиями;
- собственные функции задачи Штурма – Лиувилля с условиями, соответствующими рассматриваемым граничным условиями;

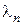 - собственные числа задачи Штурма-Лиувилля;
- собственные числа задачи Штурма-Лиувилля;  - коэффициенты, определяемые по начальным условиям.
- коэффициенты, определяемые по начальным условиям.
5) Смешанная задача для неоднородного уравнения теплопроводности
 .
.
Ее решение можно получить в виде разложения по собственным функциям задачи Штурма-Лиувилля

где 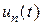 - решение задачи Коши
- решение задачи Коши
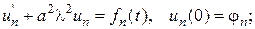
 - коэффициенты разложений
- коэффициенты разложений
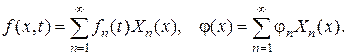
6) Смешанные задачи для волнового уравнения и уравнения теплопроводности с неоднородными граничными условиями

Каждая из этих задач сводится к задаче с однородными граничными условиями для функции
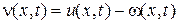
где
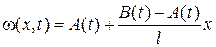
Решение получается в виде
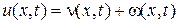
7) Краевая задача для уравнения Лапласа в круговом секторе

(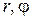 - полярные координаты,
- полярные координаты, 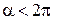 ):
):
- дифференциальное уравнение  ,
,
-граничные условия
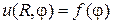 , (11.1)
, (11.1)
 . (11.2)
. (11.2)
Вместо (11.2) рассматриваются и условия
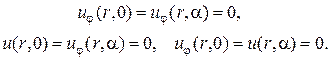 (11.3)
(11.3)
Решение задачи по методу Фурье получается в виде
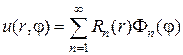
где 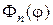 - собственные функции задачи Штурма-Лиувилля для дифференциального уравнения
- собственные функции задачи Штурма-Лиувилля для дифференциального уравнения

с условиями, соответствующими рассматриваемым граничным условиям вида (11.2) и (11.3);
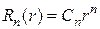
 - коэффициенты, определяемые по граничным условиям (11.1).
- коэффициенты, определяемые по граничным условиям (11.1).
8) Задача Дирихле для уравнения Лапласа в круге
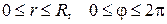
 - полярные координаты):
- полярные координаты):
- дифференциальное уравнение  ;
;
- граничное условие 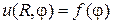 .
.
Решение этой задачи по методу Фурье получается в виде
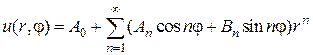
где 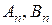 - коэффициенты, определяемые по граничным условиям.
- коэффициенты, определяемые по граничным условиям.
Приложения
Приложение 1
Таблица эквивалентных бесконечно малых функций
и асимптотических разложений (при 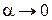 )
)
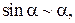
| 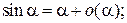
|
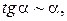
| 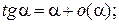
|

| 
|
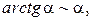
| 
|
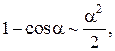
| 
|
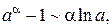
| 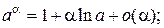
|
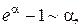
| 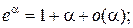
|
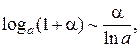
| 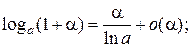
|
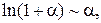
| 
|
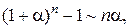
| 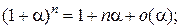
|

| 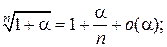
|
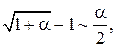
| 
|
Приложение 2
Таблица производных
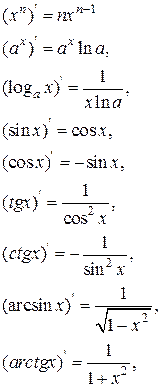
|
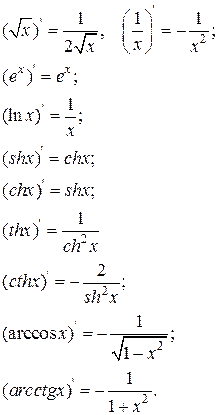
|
Приложение 3
Правила дифференцирования
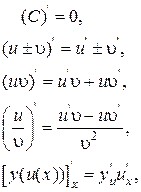
|
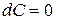 (С- постоянная); (С- постоянная);
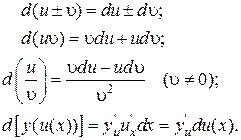
|
Приложение 4
Таблица интегралов
 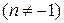 , ,
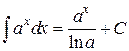 , ,

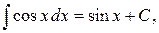
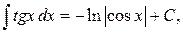

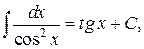
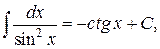
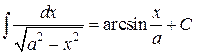 
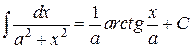

|


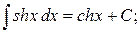
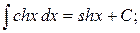
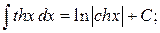
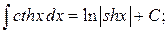
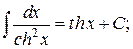
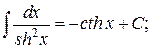
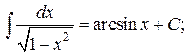
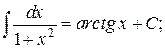
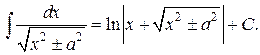
|
Приложение 5




