Типовой расчет по высшей математике №2 для 1 курса
«Аналитическая геометрия» 
Вариант 1.
1.Принадлежат ли точки М1(4, -4, 3), М2(3,-3,3), М3(5,5,0)
прямой  , где
, где 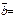 (1,-1,0),
(1,-1,0),  = (2,-2,3).
= (2,-2,3).
2.Записать уравнение прямой, проходящей через заданные точки:
а) М1 (2, -3, 2) и М2(1, 4, 0);
б) М1(5, -6, 0) и М2(1, 2, 3);
в) М1(3, -2, 1) и М2(-1, 1, 4).
3. Через точку  (-2, 0, 3) провести прямую параллельно заданной прямой:
(-2, 0, 3) провести прямую параллельно заданной прямой:


4.Записать уравнение прямой, проходящей через точки М1(2, 2) и
М2(-2, 4).
5. Через точку  (0, -4) провести прямые:
(0, -4) провести прямые:
а) параллельно прямой 2х+3y-2=0
б) перпендикулярно прямой 3x-5y+8=0
в) перпендикулярно к оси ОХ
г) перпендикулярно к оси ОY.
6.Записать уравнение плоскости проходящей через:
а) точку М(8, -1, 4) перпендикулярно вектору  =(2, -4, 3)
=(2, -4, 3)
б) три точки: М1(1, 2, 3), М2(3, 2, 1) и М3(2, 1, 3)
в) точку М(2, 3, 4) и прямую

г) непараллельные прямые
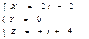 и
и 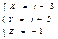
д) две параллельные прямые
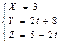 и
и 
7.Найти точку пересечения
прямой  с плоскостью x-3y+5z+9=0.
с плоскостью x-3y+5z+9=0.
8.Найти точку М1, симметричную точке М0(2, 2, 4)
относительно плоскости x+y+4z-8=0
Типовой расчет по высшей математике №2 для 1 курса
«Аналитическая геометрия» 
Вариант 1.
1.Принадлежат ли точки М1(4, -4, 3), М2(3,-3,3), М3(5,5,0)
прямой  , где
, где 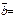 (1,-1,0),
(1,-1,0),  = (2,-2,3).
= (2,-2,3).
2.Записать уравнение прямой, проходящей через заданные точки:
а) М1 (2, -3, 2) и М2(1, 4, 0);
б) М1(5, -6, 0) и М2(1, 2, 3);
в) М1(3, -2, 1) и М2(-1, 1, 4).
3. Через точку  (-2, 0, 3) провести прямую параллельно заданной прямой:
(-2, 0, 3) провести прямую параллельно заданной прямой:


4.Записать уравнение прямой, проходящей через точки М1(2, 2) и
М2(-2, 4).
5. Через точку  (0, -4) провести прямые:
(0, -4) провести прямые:
а) параллельно прямой 2х+3y-2=0
б) перпендикулярно прямой 3x-5y+8=0
в) перпендикулярно к оси ОХ
г) перпендикулярно к оси ОY.
6.Записать уравнение плоскости проходящей через:
а) точку М(8, -1, 4) перпендикулярно вектору  =(2, -4, 3)
=(2, -4, 3)
б) три точки: М1(1, 2, 3), М2(3, 2, 1) и М3(2, 1, 3)
в) точку М(2, 3, 4) и прямую

г) непараллельные прямые
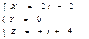 и
и 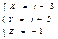
д) две параллельные прямые
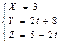 и
и 
7.Найти точку пересечения
прямой  с плоскостью x-3y+5z+9=0.
с плоскостью x-3y+5z+9=0.
8.Найти точку М1, симметричную точке М0(2, 2, 4)
относительно плоскости x+y+4z-8=0
Типовой расчет по высшей математике №2 для 1 курса
«Аналитическая геометрия» 
Вариант 2.
1.Принадлежат ли точки М1(5, 5, 5), М2(-1,3,-1), М3(5,-5,9)
прямой  , где
, где 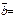 (3,-4,5),
(3,-4,5),  = (-1,3,-1).
= (-1,3,-1).
2.Записать уравнение прямой, проходящей через заданные точки:
а) М1 (-1, 2, -3) и М2(4, -1, 0);
б) М1(-5, -2, 0) и М2(-12, 7, -1);
в) М1(2, -4, -3) и М2(5, -6, 0).
3. Через точку  (-1, 3, -3) провести прямую параллельно заданной прямой:
(-1, 3, -3) провести прямую параллельно заданной прямой:


4.Записать уравнение прямой, проходящей через точки М1(-1, 3) и
М2(5, 0).
5. Через точку  (0, 1) провести прямые:
(0, 1) провести прямые:
а) параллельно прямой 6х+y+13=0
б) перпендикулярно прямой –x+5y=0
в) перпендикулярно к оси ОХ
г) перпендикулярно к оси ОY.
6.Записать уравнение плоскости проходящей через:
а) точку М(1, -1, 8) перпендикулярно вектору  =(-4, -3, 10)
=(-4, -3, 10)
б) три точки: М1(1, 2, -3), М2(1, 0, 1) и М3(-2, -1, 6)
в) точку М(-4, -3, 10) и прямую

г) непараллельные прямые
 и
и 
д) две параллельные прямые
 и
и 
7.Найти точку пересечения
прямой  с плоскостью 3x-2y+5z-3=0.
с плоскостью 3x-2y+5z-3=0.
8.Найти точку М1, симметричную точке М0(2, 2, 4)
относительно прямой 
Типовой расчет по высшей математике №2 для 1 курса
«Аналитическая геометрия» 
Вариант 2.
1.Принадлежат ли точки М1(5, 5, 5), М2(-1,3,-1), М3(5,-5,9)
прямой  , где
, где 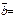 (3,-4,5),
(3,-4,5),  = (-1,3,-1).
= (-1,3,-1).
2.Записать уравнение прямой, проходящей через заданные точки:
а) М1 (-1, 2, -3) и М2(4, -1, 0);
б) М1(-5, -2, 0) и М2(-12, 7, -1);
в) М1(2, -4, -3) и М2(5, -6, 0).
3. Через точку  (-1, 3, -3) провести прямую параллельно заданной прямой:
(-1, 3, -3) провести прямую параллельно заданной прямой:


4.Записать уравнение прямой, проходящей через точки М1(-1, 3) и
М2(5, 0).
5. Через точку  (0, 1) провести прямые:
(0, 1) провести прямые:
а) параллельно прямой 6х+y+13=0
б) перпендикулярно прямой –x+5y=0
в) перпендикулярно к оси ОХ
г) перпендикулярно к оси ОY.
6.Записать уравнение плоскости проходящей через:
а) точку М(1, -1, 8) перпендикулярно вектору  =(-4, -3, 10)
=(-4, -3, 10)
б) три точки: М1(1, 2, -3), М2(1, 0, 1) и М3(-2, -1, 6)
в) точку М(-4, -3, 10) и прямую

г) непараллельные прямые
 и
и 
д) две параллельные прямые
 и
и 
7.Найти точку пересечения
прямой  с плоскостью 3x-2y+5z-3=0.
с плоскостью 3x-2y+5z-3=0.
8.Найти точку М1, симметричную точке М0(2, 2, 4)
относительно прямой 




