Анализ исходных данных.
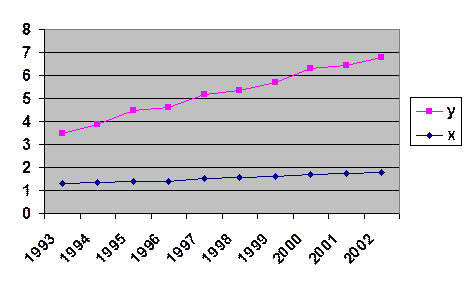
График №1. Динамика чистого дохода и капиталовложений.
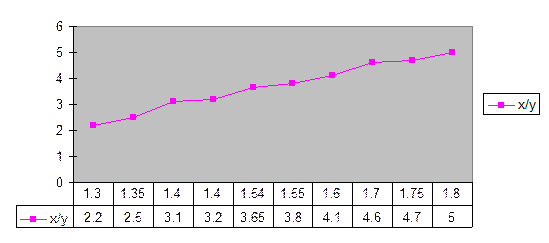 График №2. Зависимость чистого дохода и капиталовложений.
График №2. Зависимость чистого дохода и капиталовложений.
Построение модели.
Используя МНК, решаем систему нормальных уравнений.
na0+a1∑x=∑y
a0∑x+a1∑x 2 =∑xy
10a0+15,39a1=36,85
15,39a0+23,96a1=58,17
Решим систему по правилу Крамера.
D0 =  D1 =
D1 =  D3 =
D3 = 
D0 = 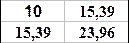 D1 =
D1 =  D3 =
D3 = 
D0=2,75; D1=-12,31; D3=14,58.
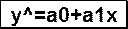
a0=D1/D0=-12,31/2,75=-4,48; a1=D3/D1=154,58/2,75=5,30.
y^=-4,48+5,30x
Модель с численными параметрами представлена в таблице №1.
Анализ качества модели.
q Анализ остатков:
y^1=-4,48+5,70x1,30=2,93 и т. д.
Построение графика изменения Е, где E=y-y^
 График№3. Анализ остатков
График№3. Анализ остатков
q Критерий «серий».
При уровне зависимости 0,05 < γ < 0,0975 количественное выражение этого правила имеет вид:
S(n)>⅓(2n-1)-1.96√(16n-29)/90,
l(n)<l0(n);
Где: n – число элементов в ряду;
S(n) – число серий;
L(n) – максимальная длина серий, при этом если n<26, то L0(n)=5, если 26<n<153, то L0(n)=6.
! по первому критерию серии требуемое условие выполняется.
q Определяем максимальную длину серии:
L(n)=3 L0=5 Ln<L0 3<5;
! По критерию серий делаем вывод, что остатки случайны и независимы. Далее можно использовать анализ регрессий.
Оценка на отсутствие автокорреляции (критерий Дарвина Уотсона).
Вычислим коэффициент Дарвина Уотсона.
DW=Σ(ei-ei-1) 2/ Σei 2
Таблица №2
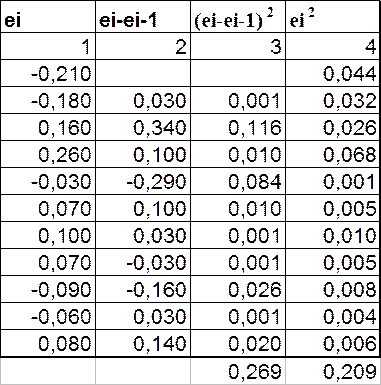
DW=0.269/0.209=1.29
Коэффициент Дарвина – Уотсона является критерием для проверки гипотезы о наличии автокорреляции в остатках в генеральной совокупности. Значения критерия DW затабулированы.
Для сравнения табличных значений и расчётных строится специальная схема:
Таблица №3

Вычисленное значение DW = 1.29 свидетельствует о том, что нет однозначного ответа и необходимо дополнительное исследование.
Корреляционный анализ.
Анализируя основной график можно сделать следующие выводы:
q Присутствует ярко выраженная линейная зависимость.
q Взаимосвязь параметров X и Y наблюдается с изменением одного параметра.
Далее определяем линейный коэффициент корреляции (R) между X и Y. Если R=1, то имеет место прямая функциональная связь, если R→0, то функциональная связь отсутствует.
r=(xy`-x`*y`)/√(x`2-(x`)2)*(y`2-(y`)2)
Корреляционный анализневозможно напрямую провести по исходным данным. Поэтому схема анализа заключается в следующем:
q Во временном ряду X и Y определяются тренды.
q Находятся отклонения от тренда (остатки).
q Корреляционный анализ применяется к отклонениям от тренда.
q Делаются выводы.
r=(ex*ey`-ex`*ey`)/√(ex`2-(ex`)2)*(ey`2-(ey`)2)
Учитывая случайные параметры X и Y, упростим корреляционный анализ:
r= 0,993
! Вывод: Очень тесная корреляционная связь. На 99% вариация признака Y (объём капиталовложений) объясняется влиянием фактора X (чистый доход).
6. Проверка статистической значимости коэффициента корреляции с учётом t статистики.
Tрасч=r*√(n-2)/√ (1-r2)
tрасч=200,64
tтеор(0,05;8)=2,31
tрасч>tтабл
! Вывод: Коэффициент корреляции статистически значим.
Анализ коэффициентов регрессии.
Вычисление среднеквадратической ошибки коэффициента регрессии.
Sa1=√(∑e12/(n-k-1))*b22
b22=n/D0
Sa=√(0,04/10)*(10/2,75)=0.13
Проверка статистической значимости коэффициентов регрессии.
Ta1расч=a1/Sa1=5,30/0,13=40,77
tтеор(0,05;8)=2,31
tрасч>tтабл
! Вывод: Коэффициенты модели статистически значимы
Построение доверительных интервалов коэффициентов регрессии.
A1 – tтабл * Sa1<α<a1 + tтабл * Sa1
5,30 – 2,31 * 0,13<α<5,30 + 2,31 * 0,13
5,00<α<5,60
Доверительный интервал [5,00; 5,60]
Проверка адекватности модели.
q Определение коэффициента детерминации
R2 = 1-∑ e12/∑ (y-y`) 2
Таблица №4
| y-y` | (y-y`)2 |
| -1,46 | 2,13 |
| -1,16 | 1,34 |
| -0,56 | 0,31 |
| -0,46 | 0,21 |
| -0,01 | 0,00 |
| 0,14 | 0,02 |
| 0,44 | 0,20 |
| 0,94 | 0,89 |
| 1,04 | 1,09 |
| 1,34 | 1,80 |
| 7,98 |
R2 = 1-0,04/7,98=0,99
Оценка статистической значимости коэффициента детерминации
Fрасч= [R2 (n-2)]/[(1- R2)*k]=792
Fтабл=239
Fрасч>Fтабл
! Вывод: Коэффициенты детерминации значимы. Модель адекватна.
Визуальная оценка точности подбора функции регрессии на основе сопоставления графиков.
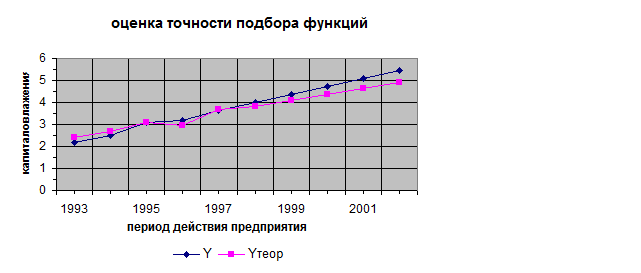 График№4. Оценка точности подбора функции
График№4. Оценка точности подбора функции






