Как известно, условием равновесия является минимум термодинамического потенциала. Самопроизвольно в системе могут идти только такие процессы, при которых термодинамический потенциал Z уменьшается. При этом равновесие не будет нарушено:
Z = U – TS + PV,
где U – внутренняя энергия;
S – энтропия;
V – объем;
T – абсолютная температура;
P – давление.
Если система состоит из двух фаз, то при постоянных T и P, ее термодинамический потенциал складывается из термодинамических потенциалов этих фаз, то есть он обладает свойством аддитивности. Это следует из аддитивности U, S и V. Свойство аддитивности термодинамического потенциала относится и к многофазным системам при любом числе компонентов.
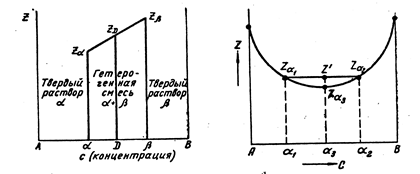
На рис. 1, а показана изотерма Z для двухфазной смеси a+b при постоянной температуре. Гетерогенный сплав D, находящийся в двухфазной области a+b, имеет потенциал ZD. Соответствующая точка лежит на прямой линии между Za и Zb.
|
|
|
а б
Рис. 1. Зависимость термодинамического потенциала
от состава сплава
В области твердого или жидкого раствора кривая зависимости термодинамического потенциала от состава сплава Z(c) обращена выпуклостью к оси абсцисс (рис. 34, б). Докажем это. Раствор произвольного состава a3 имеет потенциал Za3. Если бы он распался на две фазы a1 и a2, то по правилу аддитивности его потенциал равнялся бы Z¢, но Z¢ > Za3. Следовательно, условием равновесия однофазных сплавов действительно является зависимость Z(c), описываемая кривой, обращенной своей выпуклостью на любом ее участке к оси абсцисс.
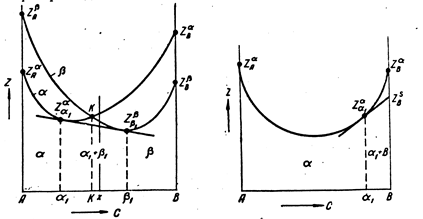
Равновесие двух растворов при постоянных давлении и температуре описывается общей касательной к кривым Z(c) каждой фазы (рис. 2, а). Из рис. 2, а видно, что минимальное значение Z в области составов от a 1 до b 1 получается для двухфазной смеси a 1 + b 1, где a 1 и b 1 – предельные растворы при данных температуре и давлении. Слева и справа на диаграмме расположены гомогенные области растворов a 1 и b, в средней ее части смесь растворов предельной концентрации a1 и b1.
Минимум Z описывается ломанной ZaА – Zaa1 –– Zbb1 – ZbВ. ZaА обозначает термодинамический потенциал фазы a, состоящей из 100 % А (чистый металл), Zaa1 – то же, для раствора предельной концентрации a 1 (фаза a) и т. п.
|
|
|
|
|
а б
Рис. 2. Зависимость термодинамического потенциала от состава
сплавов, образующих ограниченные растворы: а – растворы a и b и гетерогенные смеси a 1+ b 1; б- растворы a и гетерогенные смеси a+b
Растворы a и b могут быть твердыми или жидкими, или один из них твердым, а другой жидким.
Если оба они твердые, то рис. 2, а относится к равновесию аллотропических модификаций. Если a – твердый раствор, а b – жидкий (или наоборот), то рис. 2, а характеризует равновесие жидкого и твердого растворов при заданных Т и Р.
Проведя касательную, можно найти минимальные значения Z для равновесия твердого или жидкого раствора с металлом компонентом (однокомпонентной твердой фазой), выпавшим из этого раствора. Из рис. 2, б видно, что при заданных температуре и давлении минимальное значение термодинамического потенциала описывается ломанной ZαА – Zαα1 – ZSВ. Здесь a – твердый или жидкий раствор, а В – чистый металл, выпадающий из раствора при заданных Т и Р, находящийся с ним в равновесии в области a 1 + В, где a 1 – насыщенный раствор. Здесь ZSВ. – потенциал металла В в твердом состоянии, ZaВ –
в жидком состоянии, ZSВ < ZaВ.
Потенциал ZaВ может относиться и к твердому состоянию, характеризующемуся другой пространственной решеткой В.
Другими словами, В может быть в двух аллотропических разновидностях – S и a. При заданных на рис. 2, б значениях Т и Р устойчива разновидность S.
В состоянии a компоненты А и В изоморфны и образуют твердый раствор. Если бы он был неограниченным, кривая ZaА – ZaВ характеризовала бы непрерывную растворимость в твердом состоянии (пространственная решетка a).
В данном случае (рис. 2, б) на участке составов a 1 – В имеет место выпадение чистого В (в состоянии S) из твердого a -раствора.
Полная растворимость в твердом состоянии возможна только при изоморфных компонентах. Часто систему из таких компонентов также называют изоморфной.
На рис. 3 показаны кривые термодинамического потенциала Z для твердых и жидких растворов жидкой фазы лежит ниже кривой твердой фазы.
При низких температурах (Т4 и ниже) кривая Z жидкой фазы лежит выше, чем кривая твердой фазы. Это значит, что при низких температурах стабильны твердые растворы.
Между температурами плавления компонентов А и В (Т1 и Т4) кривые жидкой и твердой фаз пересекаются и проведением к ним общей касательной можно найти составы жидкой и твердой фаз, находящихся в равновесии при той или иной температуре.
Снизу на рис. 3 показана диаграмма равновесия в координатах температура – состав.
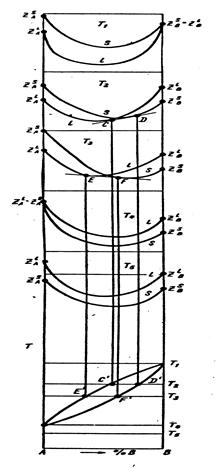
Рис. 3. Зависимость термодинамического
потенциала от состава
и температуры и диаграмма равновесия сплавов из
компонентов, неограниченно растворимых в жидком
и твердом состояниях