-11-
Определение. Поверхностью 2-ого порядка в Е 3 называют множество точек, декартовы координаты x, y и z которых удовлетворяют уравнению вида
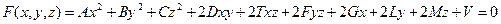, (35)
где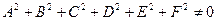 
.
Как и для кривых 2-ого порядка можно найти специальную д.пр.с.к.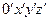 
, в которой оно принимает наиболее простой вид, позволяющий исследовать форму этой поверхности. Такой вид уравнений поверхностей 2-ого порядка называют каноническими. Всего существует 17 типов поверхностей 2-ого порядка, среди которых есть мнимые, например, 
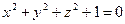или распадающиеся на пару параллельных плоскостей 
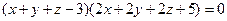. Рассмотрим вещественные нераспадающиеся поверхности 2-ого порядка.
1) Цилиндрические поверхности
Определение. Цилиндрической поверхностью (S) или цилиндром называется поверхность, которая образована множеством параллельных прямых L, называемых образующими, и пересекающих некоторую кривую K, называемую направляющей цилиндра.
Пусть образующие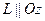 
. Тогда 
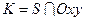, где
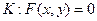(36).
Возьмем любую точку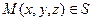 
. Точка 
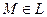. Следовательно, точка 
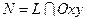лежит на K, и потому ее координаты x и y удовлетворяют уравнению (36). Но точка М имеет те же координаты x и y, что и точка 
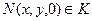, следовательно, уравнению (36) удовлетворяют и координаты x, y точки
-12-
при любом значении z. А так как М - любая точка на цилиндре S, то уравнение (36) является уравнением и для (S):
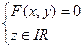, т.е. 
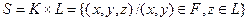.-декартово произведение K и L.
Теперь ясно, что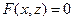 
- уравнение цилиндра, когд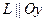а 
, а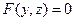 
- уравнение цилиндра при условии, что 
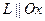. Название цилиндра определяется названием его направляющей K. Таким образом, получаем уравнения цилиндров:
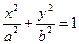- эллиптический цилиндр;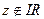 
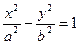- гиперболический цилиндр;
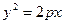- параболический цилиндр;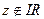
2) Конические поверхности
-13-
Определение. Конической поверхностью (S) или конусом называется поверхность, образованная множеством прямых (образующих L), проходящих через одну и ту же точку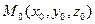 
- вершину конуса и пересекающих заданную кривую K (направляющую), не содержащую точку М 0.
Без ограничения общности можно считать, что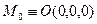 
, а K лежит в плоскости П: 
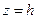, т.е. 
: .
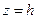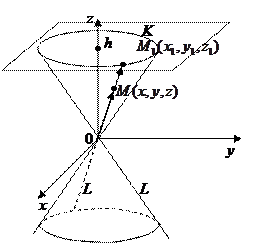Возьмем любую точку 
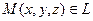и пусть 
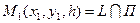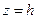(). Тогда
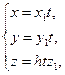(37)
так как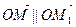 
.
Подставляя (37) в уравнение для K: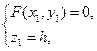 
найдем уравнение для (S). Действительно, пусть, например,
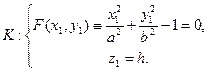(38)
Тогда из (37) и (38) получаем уравнение
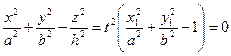или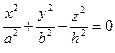 
(39) - эллиптического конуса с вершиной в точке О.
3) Поверхности вращения
Определение. Поверхность (S), образованная вращением некоторой плоской кривой L вокруг оси l, лежащий в ее плоскости, называется поверхностью вращения.
Пусть кривая L лежит в плоскости Ozy:
-14-
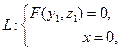(40)
и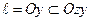 
.
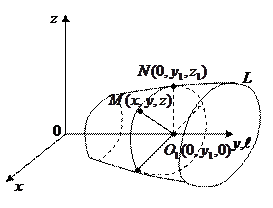Возьмем любую точку 
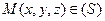. Она лежит на окружности с центром в точке 
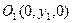и радиуса 
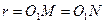. Но 
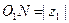, а
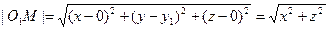, так как 
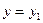для точки М. Поэтому
.
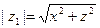Таким образом, имеем
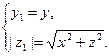(41)
Подставляя (41) в (40), получим уравнение поверхности вращения
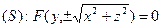. (42)
Если ту же кривую L вращать вокруг оси Oz, то уравнение поверхности вращения примет вид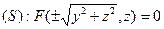 
. (43)
Например, если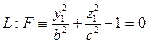 
- эллипс, то из (42) получаем
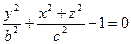или
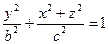. (44)
Эту поверхность называют эллипсоидом вращения.
4) Эллипсоидом называется поверхность, уравнение которой имеет вид
, а > 0, b > 0, с > 0. (45)
-15-
Эллипсоид вращения (44) - частный случай поверхности (45). Форма эллипсоида исследуется методом сечений плоскостям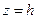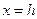и , 
и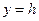 
, 
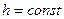. Так как эллипсоид симметричен относительно осей Ox, Oy, Oz и плоскостей Oxy, Oxz, Oyz, то достаточно рассмотреть линию сечения 
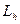его с плоскостью :
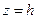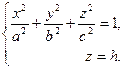(46)
Если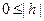 
< с, то из (46) получаем в сечении эллипс :
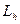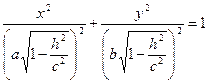(47)
с полуосям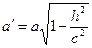и 
и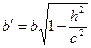 
в плоскости (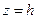). Числа 
, 
, 
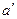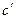называют полуосями эллипса 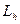. При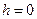 
уравнение (46) примет вид
.
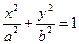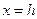Аналогично исследуется сечение эллипсоида с плоскостями и 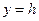, которые позволяют изобразить эллипсоид как замкнутую овальную поверхность.
5) Однополосным гиперболоидом называется поверхность, задаваемая уравнением
-16-
. (48)
Из (48) следует, что координатные плоскости служат плоскостями симметрии однополосного гиперболоида, а начало координат О - центром его симметрии. В сечении с координатными плоскостям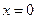и 
и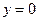 
получим гиперболы
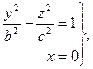(49)
и 
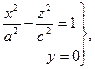(50)
а при сечении плоскостью 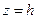получаем эллипс :
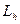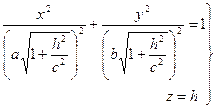. (51)
Оказывается, что однополосный гиперболоид составлен в отличие от эллипсоида из двух семейств прямых. Если рассмотреть прямые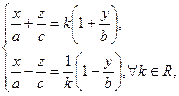 
где а, b, с -полуоси однополосного гиперболоида, то, перемножая эти равенства, получим уравнение (48).
|
|
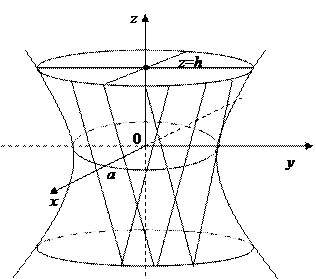Аналогично определяется второе семейство прямых 
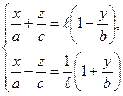для однополосного гиперболоида. При этом через каждую точку
-17-
однополосного гиперболоида проходит по одной прямой из каждого из указанных семейств.
6) Двуполосный гиперболоид можно задать уравнением
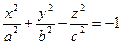. (52)
|
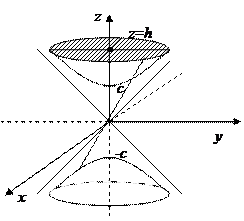Из (52) видно, что координатные плоскост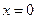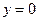и , и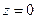 
служат плоскостями симметрии, а начало координат - центром симметрии. С осью Oz двуполосный гиперболоид пересекается в точках 
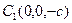и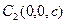 
- вершинах. С осями Ox и Oy точек пересечения нет. Плоскость 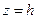, | h |> с, пересекает двуполосный гиперболоид по эллипсу :
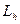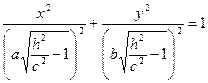, а в сечении с плоскостям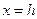и и 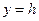получаем гиперболы, в частности, есл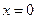и и 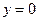, то эти гиперболы
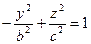и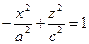 
.
7) Эллиптическим параболоидом называют поверхность, задаваемую уравнением
, 
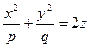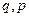> 0. (53)
Так как в уравнении (53) координаты x и y входят в четных степенях, то поверхность имеет две плоскости симметрии Oyz и Oxz. Из (53) видно, что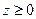 
, т.е. поверхность проходит через начало координат О (0,0,0) и лежит выше плоскости Oxy. Сечение (53) с плоскостью 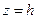, h > 0, - эллипс :
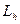-18-
|
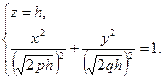
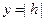Сечения поверхности (53) с плоскостями 
и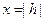 
являются параболами, в частности пр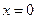и и 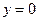- это параболы
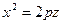и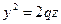 
.
При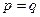 
получаем параболоид вращения.
8) Гиперболический параболоид - поверхность, задаваемая уравнением
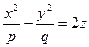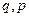, > 0. (54)
Из (54) видно, что гиперболический параболоид имеет две плоскости симметрии - Oxz и Oyz и проходит через начало координат О.
Рассечем поверхность (54) плоскостями 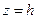. Получим кривую сечения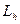 
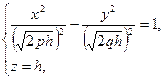которая при 
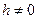является гиперболой.
При 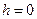- это две пересекающиеся прямые 
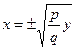. При пересечении поверхности плоскостям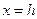и и 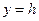получаются параболы
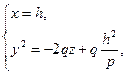
ветви которых направлены вниз, и параболы
-19-
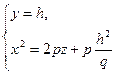
с ветвями, направленными вверх.
Таким образом, поверхность (54) имеет вид седла. Как и в случае однополосного гиперболоида можно показать, что через каждую точку гиперболического параболоида проходит по одной из прямых каждого из двух семейств прямых:
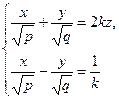и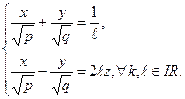 
Замечание 1. Однополосный и гиперболический параболоиды являются как и цилиндры и конусы линейными поверхностями, так как они составлены из семейства прямых линий; куски таких поверхностей обладают большой жесткостью к внешним воздействиям, например, телевизионная башня Шухова В.Г. в г. Москва (была сооружена с помощью балок, расположенных по прямолинейным образующим однополосного гиперболоида).
Замечание 2. Хотя метод координат, лежащий в основе аналитической геометрии, вводится вполне естественно, но сам факт обоснования его вовсе не очевиден, даже в случае введения координаты на прямой. Обоснование метода координат на прямой производится с помощью системы аксиом, лежащих в основании геометрии, и которые делятся на пять групп:
Группа 1 содержит восемь аксиом принадлежности планиметрии (стереометрии).
-20-
Например, каковы бы ни были точки А и В $ прямая, проходящая через них.
Группа 2 содержит четыре аксиомы порядка планиметрии (стереометрии).
Например, что среди трех точек одной прямой $ не более одной, лежащей между ними.
Группа 3 содержит 5 аксиом конгруэнтности, например, если отрезк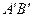и 
и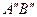 
конгруэнтны одному и тому же отрезку АВ, то они конгруэнтны между собой.
Группа 4 содержит 2 аксиомы непрерывности (аксиома Архимеда и аксиома линейной полноты).
С помощью этих четырех групп аксиом можно обосновать метод координат, используемый в аналитической геометрии.
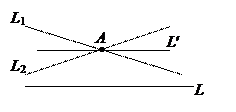Имеется еще одна аксиома из группы 5, которая играет фундаментальную роль в обосновании самой геометрии. Это аксиома Евклида о параллельности: в плоскости, определяемой прямой L и точкой 
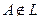существует не более одной прямой, проходящей через А и не пересекающей L. Много столетий пытались доказать эту аксиому на основании аксиом групп 1-4. В 1826г. русский геометр Н.И. Лобачевский сделал доклад о своем, одном из самых выдающихся открытий в науке, в котором к аксиомам группа 1-4 он присоединил утверждение, отрицающее аксиому Евклида, и показал, что полученная геометрия является непротиворечивой, как и геометрия Евклида. Впоследствии эту геометрию назвали неевклидовой геометрией Лобачевского, согласно которой сумма внутренних углов треугольника Ð2 p. Это находит подтверждение для расстояний, сравнимых с расстояниями от Земли до Солнца, а на малых расстояниях геометрия Лобачевского практически неотличима от геометрии Евклида.
